An Introduction to Graph Neural Networks

Last updated: March 18, 2024

Reviewed by: Michal Aibin
Baeldung Pro – CS – NPI EA (cat = Baeldung on Computer Science)
announcement - icon

Learn through the super-clean Baeldung Pro experience:

>> Membership and Baeldung Pro.

No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.

1. Introduction

In recent years, the field of artificial intelligence has witnessed a surge in the development and application of deep learning techniques. While deep learning has revolutionized many areas, such as image recognition and natural language processing, it has faced challenges in effectively handling structured data, particularly graph-structured data. To address these challenges, a groundbreaking technique called Graph Neural Networks (GNNs) has emerged. GNNs enable machines to understand better and process graph-structured data.

In this tutorial, we’ll provide a comprehensive introduction to GNNs, exploring their architecture, training process, and various applications.

2. Understanding Graphs

Before delving into GNNs, it is crucial to grasp the fundamentals of graphs. A graph is composed of nodes (also known as vertices) connected by edges (also called links or relationships). Nodes represent entities, while edges represent relationships or interactions between these entities. Graphs can be either directed (edges have a specific direction) or undirected (edges are bidirectional). Additionally, graphs may incorporate various attributes or features associated with nodes and edges, providing additional information to enhance learning.

Let’s discover the intricate Jazz Musicians Network dataset, featuring 198 nodes and 2742 edges. The visualization below illustrates distinct communities of Jazz musicians, identified by diverse node colors and connecting edges. This web of connections highlights both intra-community and inter-community collaborations among musicians:

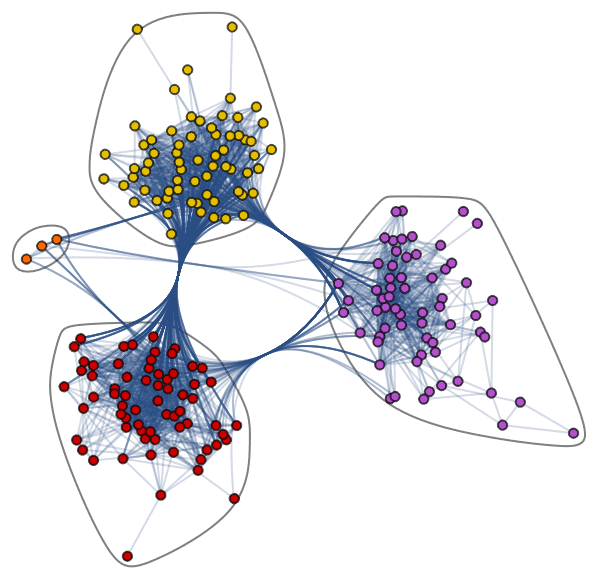
Community Graph Plot by Jazz Musicians Network

Graphs are particularly adept at tackling intricate challenges involving relationships and interactions. They find applications in diverse domains such as pattern recognition, social network analysis, recommendation systems, and semantic analysis. The development of solutions rooted in graph-based methodologies represents an emerging field that promises profound insights into the complexities of interconnected datasets.

3. What Is a GNN?

GNNs are a class of deep learning models designed to process and analyze graph-structured data. GNNs leverage the inherent structural information of graphs to learn powerful node and graph representations, enabling them to capture complex dependencies and propagate information effectively across the graph.

GNNs are strongly influenced by graph embedding and Convolutional Neural Networks, and graph embedding have a strong impact on them. GNNs are applied to make predictions concerning nodes, edges, and tasks based on graphs.

4. GNN Architecture

The architecture of a GNN consists of multiple layers, each responsible for aggregating and updating information from neighboring nodes. The core idea behind GNNs is the “message-passing” paradigm, where information is exchanged between nodes during the training process. At each layer, the GNN performs two fundamental steps:

  • Message passing: In this step, every node aggregates information from its neighboring nodes, which is then transformed into an informative message. The message typically consists of information from the node’s own features and the features of its neighbors
  • Node update: The node utilizes the received messages to update its internal representation or embedding. This step enables nodes to incorporate information from their local neighborhood and refine their representation

By iteratively repeating the message passing and node update steps, the GNN enables information to propagate across the entire graph, allowing nodes to learn and refine their embeddings collectively.

5. Differences Between GNN, CNN, and RNN

The below table summarizes the differences between GNN, Convolutional Neural Networks (CNNs), and Recurrent Neural Networks (RNNs) based on various aspects:

Aspect GNNs CNNs RNNs
Input type Graphs (nodes, edges, features) Grid-like data (e.g. images) Sequential data (e.g. time series)
Information Flow Propagates information across nodes Local receptive fields in convolution Information passed sequentially
Architecture Message passing, node update Hierarchical layers of convolutions Sequential layers of neurons
Memory of past data Incorporates global graph structure Captures local patterns in the grid Captures temporal dependencies
Applications Social networks, molecular structures Image recognition, computer vision Natural language processing, speech
Training complexity Moderate complexity due to graphs Complex, numerous layers, large data Complex due to sequential dependencies
Parallel Processing Limited due to graph structure High due to parallel convolutions Limited due to sequential nature
Data size tolerance Sensitive to graph size and structure Less sensitive, scales with data Sensitive to sequence length

In summary, GNNs are designed for graph data, CNNs for grid-like data, and RNNs for sequential data. Each architecture has its strengths and weaknesses, making them better suited for specific tasks and types of input data.

6. Types of GNNs

GNNs come in various forms, each tailored to handle specific types of graph-structured data. Some common types of GNNs include:

  • Graph Convolutional Networks (GCNs): GCNs are one of the earliest and most widely used GNN variants. They leverage graph convolutions to aggregate and update node representations based on their local neighborhood
  • GraphSAGE: GraphSAGE (Graph Sample and Aggregated) is another popular GNN architecture. It utilizes a sampling strategy to aggregate and update node embeddings, allowing for scalability in large graphs
  • Graph Attention Networks (GATs): GATs introduce attention mechanisms into GNNs, enabling nodes to selectively attend to relevant neighbors while performing message passing and aggregation
  • Graph Isomorphism Networks (GINs): GINs focus on capturing the structural information of graphs by applying permutation-invariant functions during the message passing and node update steps

7. Training GNNs

Training a GNN involves a series of mathematical operations that facilitate the propagation of information through nodes and edges. This section will delve into the mathematical foundations of training GNNs, providing insights into the formulas and processes that drive their learning process.

Before diving into the math, let’s briefly review the architecture of a GNN. As discussed above, a GNN consists of multiple layers comprising two main steps: message passing and node update. These steps are performed iteratively to allow information to flow across the graph. The key lies in the mathematical expressions that govern these steps.

7.1. Message Passing

At each layer of a GNN, the message-passing step involves aggregating information from neighboring nodes. Mathematically, for node v at layer k, the aggregated message m_{v}^{k} is calculated as a function of the embeddings of its neighbors N(v):

    \[m_{v}^{k}=\sum_{u\in N(v)}M^{k}\left(h_{u}^{k-1},h_{v}^{k-1},e_{uv}\right),\]

where M^{k} represents a message aggregation function at layer k, h_{u}^{k-1} and h_{v}^{k-1} are the embeddings of nodes u and v at the previous layer, and e_{uv} represents any edge-specific attributes.

7.2. Node Update

After aggregating messages, the node update step involves using these messages to update the node’s representation. This is done through a function U^{k}:

    \[h_{v}^{k}=U^{k}\left(h_{v}^{k-1},m_{v}^{k}\right),\]

where U^{k} is the node update function at layer k.

7.3. Training GNNs with Backpropagation

Training a GNN aims to learn the optimal parameters that allow the network to make accurate predictions or classifications based on graph-structured data. This is typically achieved through a supervised learning process using a loss function. The most common approach is to employ backpropagation and gradient descent to optimize the GNN’s parameters.

8. Capability of GNNs

Below, we outline the capability of GNNs in handling various machine learning tasks:

  • Graph classification: this task requires classifying graphs into different categories. Applications of this task include social network analysis and text classification
  • Node classification: this task uses neighboring node labels for the prediction of missing node labels in a graph
  • Link prediction: in this task, the link between a pair of nodes in a graph is predicted, given an incomplete adjacency matrix. This task is commonly used for social networks
  • Community detection: in this task, graph nodes are divided into various clusters based on edge structure. The learning inputs include edge weights, distance, and graph objects similarly
  • Graph embedding: this task maps graphs into vectors, preserving the relevant information on nodes, edges, and structure
  • Graph generation: taking sample graph distribution as input to learn how to generate a new but similar graph structure

9. Applications of GNNs

The versatility of GNNs has led to their successful application in various domains, including:

  • Social network analysis: GNNs can model relationships in social networks, enabling tasks such as link prediction, community detection, and recommendation systems
  • Bioinformatics and drug discovery: GNNs have shown promising results in predicting molecular properties, protein-protein interactions, and aiding in the discovery of new drugs
  • Knowledge graphs: GNNs can enhance knowledge graph embeddings, enabling better representation learning and link prediction in knowledge graphs
  • Recommendation systems: GNNs can capture user-item interactions and improve the accuracy of recommendation systems by leveraging graph-structured user-item data

10. Conclusion

In this article, we provided a comprehensive introduction to GNNs, exploring the architecture and training process of GNNs, as well as various applications. As research in this field continues to advance, we can expect GNNs to play an increasingly vital role in unlocking the potential of graph-structured data and paving the way for innovative applications in the future.

Graph Neural Networks have emerged as a powerful tool for processing and analyzing graph-structured data. GNNs enable machines to capture complex dependencies and propagate information effectively across nodes by harnessing the rich structural information inherent in graphs.