What Is an Incident Edge?

Last updated: March 18, 2024

Reviewed by: Michal Aibin

1. Overview

In this tutorial, we’ll discuss what an incident edge is and how it can be found in directed and undirected graphs.

2. General Idea

In general, two edges are “incident” if they share a common vertex.

Not only edges, but vertices can also be incident with an edge. A vertex is incident with an edge if the vertex is one of the endpoints of that edge.

So, let’s assume we’ve got two edges e_1 and e_2. Further, assume that the edges have a common endpoint vertex V. In this case, we can say the edges e_1 and e_2 are incident.

Alternatively, if an edge e_3 connects two vertices V_1 and V_2 then the edge is said to be incident on the vertex V_1 and V_2.

Notice that in the previous example, the vertex V is part of both the edges e_1 and e_2. In such cases, we can say that the vertex V is incident on the edges e_1 and e_2.

3. An Undirected Graph Example

In this section, let’s try to find out some incident edges from our sample directed and undirected graphs.

We’re taking on an undirected graph first:

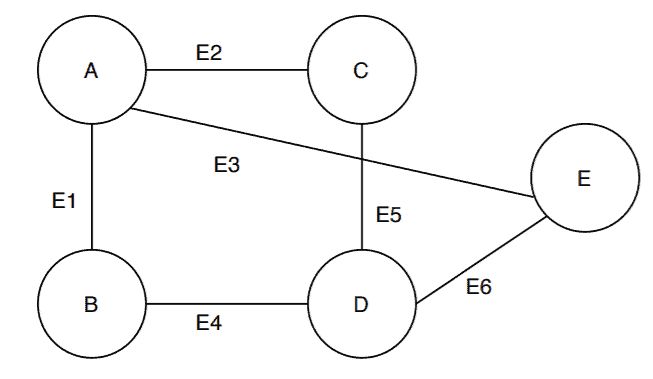
first-example

This undirected graph G_1 has a the vertex set V = (A, B, C, D, E) and an edge set E = (E_1, E_2, E_3, E_4, E_5, E_6). From this graph, let’s find out some of the incident relationship among edges and vertices:

  • The edges E_1, E_2, E_3 are incident edges as the vertex A is one of their common endpoints
  • Alternatively, the vertex A is incident on the edges E_1, E_2, E_3
  • The edges E_1 and E_4 are incident edges as the vertex B is one of their common endpoints
  • Alternatively, the vertex B is incident on the edges E_1 and E_4

Similarly, we can find other incident relationship between the edges and vertices in graph G_1.

4. A Directed Graph Example

Let’s talk about a directed graph now:

2-3

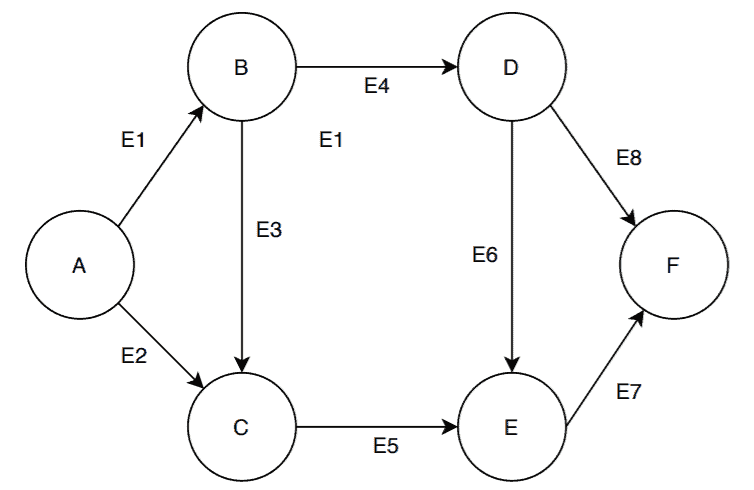
Now, we’ve taken a directed graph G_2 with the vertex set V = (A, B, C, D, E, F) and edge set E = (E_1, E_2, E_3, E_4, E_5, E_6, E_7, E_8). We’re aiming to define the incident relationship between the edges and vertices in G_2:

  • The edges E_1 and E_2 are incident as they share the common vertex A
  • The vertex A is incident on the edge E_1 and E_2
  • The edge E_1 is incident on the vertex B from the vertex A
  • Similarly, the edge E_2 is incident on the vertex C from the vertex A

Basically, the incident relationship between the vertices and edges in a directed as well as an undirected graph remains the same. The only difference is that in case of a directed graph, as the edges have directions so they are now incident on a vertex from another vertex.

5. Applications

In graph theory, if we want to calculate the degree of a vertex, we count the number of edges incident on the vertex. The total number of edges incident on a vertex is the degree of that particular vertex. So the incident edge concept is used to find out the degree of a vertex.

The incident edge concept is used in the edge coloring problem in graph theory. In edge coloring, all the edges need to fill with color such that no two incident edges have the same color.

Another use of the incident edge concept is in the edge cover problem. Edge cover consists of a set of edges and each vertex in the graph should incident on at least one of the edges from the edge cover set.

6. Conclusion

In this tutorial, we’ve discussed the incident edges and vertices in both directed and undirected graphs.

Furthermore, we’ve presented a couple of examples and mentioned some applications as well.

Comments are open for 30 days after publishing a post. For any issues past this date, use the Contact form on the site.