How to Build a Knowledge Graph? | Baeldung on Computer Science

1. Overview

In this tutorial, we’re going to discuss the problem of representation of knowledge in a computable manner. From this, we’ll derive a method for building graph-like structures for knowledge representation.

We’re also going to discuss the relationship between Knowledge Bases, expert systems, and knowledge graphs as well as the way they interact with one another.

At the end of this tutorial, we’ll be familiar with the theory behind expert systems and the symbolic approach to the development of AI. We’ll also know the procedures necessary for building knowledge graphs from Knowledge Bases.

2. The Problem of World Representation

2.1. Knowledge, Bayesian Priors, and World Representation

If we want to build a knowledge graph, we must first understand what we mean by knowledge.

We discussed in our article on the labeling of data the idea that any AI system embeds a series of hypotheses on how the world functions, and that these hypotheses are typically (but not always) hard-coded into it. These hypotheses constitute the Bayesian priors on which the system operates, and that in turn allows inferential reasoning to take place.

Another way to look at those Bayesian priors is to consider them as the knowledge that the system possesses about the world. The system must presume to know something about the world, in order to operate in it. One of these most basics assumptions is the proposition there exist objects:

These objects belong to classes that we can represent symbolically. Together these classes form an ontology or taxonomy and allow the simplification of an otherwise too-complex environment.

The complexity of the agent’s ontology represents, in turn, the complexity of its external world. A more complex environment requires more complex ontology to orient the agent’s behavior, and vice versa.

2.2. No Taxonomy Without Representation

Thanks to those hypotheses, and thanks to this knowledge, the system is capable of operating on the data that it receives from the environment and then make decisions. This decision can assume, for instance, the form of recognition of objects in the environment, according to a pre-ordained taxonomy:

The primitive knowledge that’s encoded in a machine learning system normally derives from the knowledge of the human programmers that wrote that system. On the basis of that knowledge, the system can perform further operations that allow for the expansion of its understanding of the environment. Without that knowledge, in contrast, the system can’t learn anything new or perform any operations at all:

In general, the complex of knowledge detained by an agent is called a knowledge base. One particular type of structure used to store this knowledge is knowledge graphs. It’s in this context that we study knowledge graphs, as data structures for the storage of world representations of an AI agent.

3. Encoding Knowledge

3.1. Propositional Knowledge

The knowledge that a system possesses can assume various forms. For this article, we’ll focus on a specific type of knowledge that relates to symbolic reasoning, called propositional knowledge.

Propositional knowledge is knowledge expressed in the form of logical propositions. Logic statements of the form $p \rightarrow q$ , or $a \vee b \rightarrow c \wedge d$ are all valid examples of logic propositions. These statements are empty though because we haven’t yet assigned content to them.

The content of propositional knowledge is encoded through symbols, such as words, that we imagine being connected to one another by means of a subject-predicate-object relationship. This relationship is a necessary component of any sentence encoding knowledge. Sentences of this type take the name of declarative sentences and contain factual statements about the world.

Let’s first make three examples of sentences that don’t contain knowledge:

Get over here as soon as possible (imperative, not declarative)
Did you visit the museum? (interrogative, not declarative)
I’m surprised! (exclamative, not declarative)

Let’s now make examples of propositional knowledge; to these examples, we’ll then refer for the rest of this section:

The Earth rotates around the Sun
A cow produces milk
The lemon is yellow

3.2. 3-Tuples of Knowledge

We can further break down these propositions to extract from them entities and their relationships:

The words Earth and Sun can be connected by the relationship rotates around
Cow and Milk can be connected by the relationship produces
Lemon and Yellow can be connected by the relationship is

Some special neural networks can automatically perform this task for us. The subject of named-entity recognition is a topic on its own and we won’t treat it here. We can simply assume for this article that there’s a magical way to extract nouns from sentences and to identify the relationship that links them.

If we perform this extraction on the three propositions above, we can then formulate shorter propositions that contain two words, called subject and object, and their relationship, called predicate:

Earth (subject) rotates around (predicate) Sun (object)
Cow (subject) produces (predicate) milk (object)
Lemon (subject) is (predicate) yellow (object)

We can also express the same propositions in the form of tuples, containing respectively the subject, the object, and the predicate, in that order. Some authors use the order subject, predicate, object, though, and that’s equally valid; the important thing is that we’re consistent throughout. The reason why we prefer this order is that it maps better to the definition of edges in a knowledge graph, as we’ll see later.

If we convert into tuples the sample propositions above we get this set:

(Earth, Sun, rotates around)
(cow, milk, produces)
(lemon, yellow, is)

The information content of these tuples corresponds to that of the sentences in human natural language. This time, however, that content is expressed in a computable format, and we can operate on that.

3.3. Concatenation of Tuples and Inferences

We can then take the set of propositions encoded in 3-tuples and use them to conduct inference. By chaining them together, we can form new tuples containing knowledge that wasn’t previously included in our original set of propositions. For this example, we’ll use the common logic argument around Socrates’ mortality.

Let’s start with these two sentences:

Socrates is a human
A human is a mortal

From which we can derive the following two 3-tuples of knowledge:

(Socrates, human, is)
(human, mortal, is)

By noting how the object (second element) of the first tuple is also the subject (first element) of the second tuple, we can then establish the following concatenation:

Socrates is human is mortal

This, in turn, implies that the relationship (Socrates, mortal, is) must also be true. At the end of this logic reasoning we can expand our set of 3-tuples, which now contains three elements:

(Socrates, human, is)
(human, mortal, is)
(Socrates, mortal, is)

The procedure we’ve followed allowed us to generate new knowledge, corresponding to an expansion in the set of knowledge propositions, exclusively by means of logical operations. Notice how this type of reasoning can be conducted without any understanding of what Socrates, humans, or mortality really are.

4. Expert Systems and Knowledge Bases

4.1. Expert Systems

Systems that store knowledge in a computable format and that conduct operations on them are called expert systems. The name derives from the fact that they operate as if they were experts in their discipline. Due to the lack of sectorial or subject-matter knowledge, the developers of these systems would frequently consult experts in a given discipline in order to convert their subject-matter knowledge to logical propositions, which further contributed to the name.

Expert systems embed the symbolic approach to the development of AI and date back to the 1950s. These expert systems are still in use today, but the necessity to code by hand their knowledge propositions implies that they scale poorly.

This, in turn, led to the development of automated solutions for the extraction of semantic relationships in unstructured texts. These extracted relationships are what today constitutes knowledge graphs in modern expert systems.

4.2. Knowledge Base

We can now give a definition of Knowledge Base in relation to expert systems. A Knowledge Base is the complex of knowledge, information, and data, held by an expert system.

Knowledge bases distinguish themselves from databases, and we can’t reduce one to the other. This is because databases contain what we can call results of measurements or observations that have no general validity besides that of the observation which produced them. Knowledge bases, on the other hand, contain statements or rules that are valid universally and unconditionally.

In this sense, they better represent the theoretical knowledge held by a scientist than the numbers resulting from measurements:

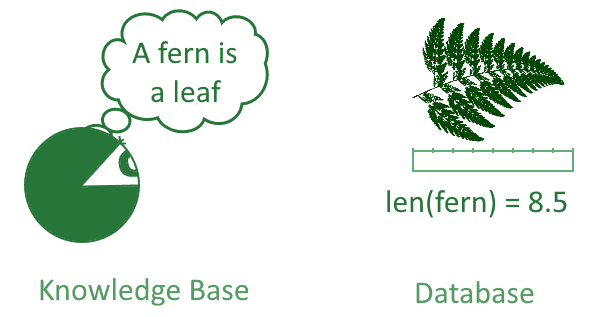
We can find Knowledge Bases in all types of information management systems, the most famous of which is probably Google’s sidebox:

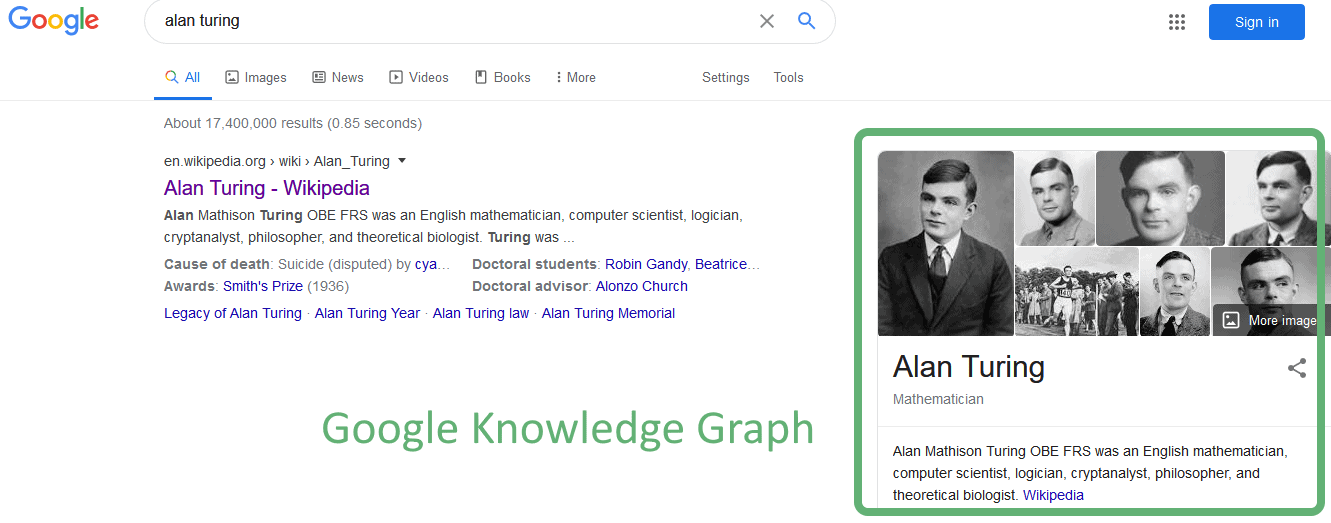
This sidebox is known as Google Knowledge Graph, but it’s in fact a full Knowledge Base, not only a graph. As of today, Google Knowledge Graph is probably the largest Knowledge Base in the world. Some consider instead the Internet as the largest Knowledge Base, but this would leave us with the paradox that most of the knowledge in the world’s largest Knowledge Base is made of cats and memes.

4.3. Non-Propositional Components of Knowledge Bases

One final note to make on the general properties of real-world Knowledge Bases is that they don’t exclusively contain propositional knowledge. They do in fact integrate relational and hierarchical databases as well as procedures for analyzing that data.

For this article, we’re however going to assume that a Knowledge Base is comprised exclusively of knowledge propositions. This, in fact, allows us to highlight interesting characteristics of the relationship between the edges of a graph and the propositions of a Knowledge Base, as we’ll see shortly.

5. Graphs for Representing Knowledge

5.1. From 3-Tuples to Multilayer Graphs

We can now move toward the construction of a knowledge graph corresponding to the propositional knowledge contained in a Knowledge Base.

Knowledge graphs are directed multilayer graphs whose adjacency matrix corresponds to the content of 3-tuples of knowledge contained in a Knowledge Base. We can build the knowledge graph from a Knowledge Base in the following manner.

First, we start with a Knowledge Base containing a set of 3-tuples representing propositional knowledge. For this section, we’ll use a small Knowledge Base related to Astronomy:

(Earth, planet, is_a)
(Sun, star, is_a)
(planet, star, rotates_around)
(planet, round, is_a)

This Knowledge Base comprises four 3-tuples that map two relationships, is_a and rotates_around, between five named entities: Earth, Sun, planet, star, and round. The relationship is_a is a typical way to express class affiliation in knowledge bases. The relationship rotates_around requires no clarification.

5.2. Building a Knowledge Graph

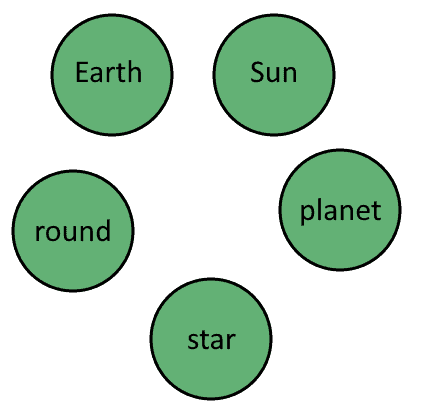
From the first two elements of these 3-tuples we can extract a set of unique named entities, which will constitute the labels of individual vertices in a knowledge graph:

$V = \{Earth, Sun, planet, star, round\}$

Notice how we discarded the two repetitions of planet and one of star since we’re interested in unique labels for vertices in a graph:

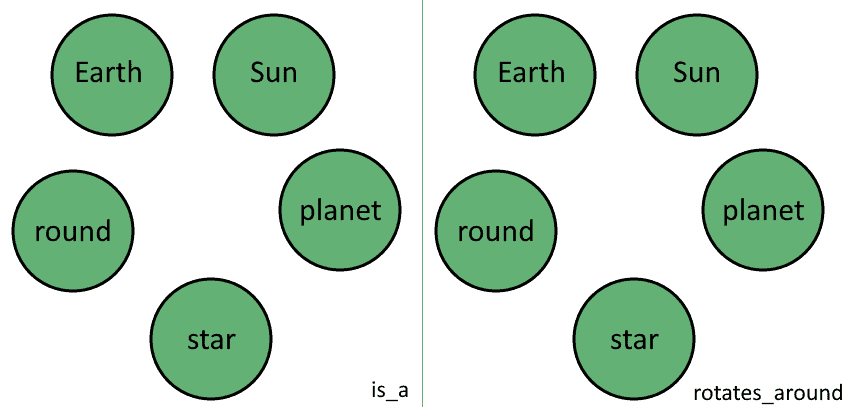
Next, we extract the list of unique relationships, contained in the third element of the 3-tuples. These are: is_a and rotates_around. As before, we’ve discarded all repetitions of the relationship is_a since we’re interested in unique relationships. The unique relationships we identified constitute the distinct discrete dimensions in the multilayer graph:

$D = \{is\_a, rotates\_around\}$

All vertices in the set $V$ exist in all dimensions $d_1, d_2, ... , d_{|D|}$ of the graph. This means that we have, for all purposes, a series of layers containing independent graphs that map to different relationships but share the same vertices:

We can finally extract the edges of these graphs. The edges map perfectly to the 3-tuples contained in the Knowledge Base: to convert from 3-tuples to edges of the form $e = (outgoing\ vertex, incoming\ vertex, dimension)$ we need to simply assign the elements of the 3-tuples to the elements of the edge according to the following conversion rule:

$e(u, v, d) = (subject, object, predicate)$

The result is a set $E = \{e_1, e_2, ..., e_m\}$ of directed edges $e = (u, v, d)$ that we can use to connect the vertices of the knowledge graph:

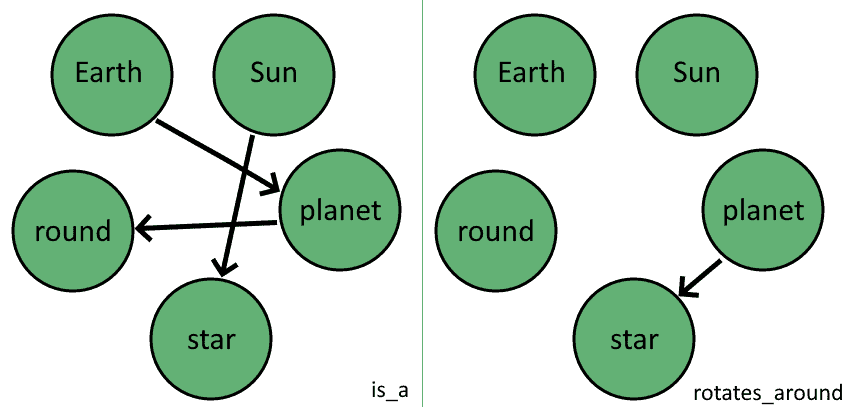
If we follow this procedure, we can convert any Knowledge Base expressed in 3-tuples of the form (subject, object, predicate) into directed multilayer graphs of the form $G(V, E, D)$ . These multilayer graphs are then what we call knowledge graphs.

5.3. Forward Chaining and Directed Paths

It’s interesting to note that the edges of the knowledge graph and the propositional knowledge contained in the Knowledge Base map 1-to-1 to one another, such that $E \mapsto KB$ . This is the reason why, if we can algorithmically discover new edges in a knowledge graph, we’re certainly able to also add new 3-tuples to the corresponding Knowledge Base.

One way to do this is to assume that, if a directed path between two vertices $(u, v)$ exists in a given layer $d$ , then the two vertices are also connected by a directed edge $e = (u, v, d)$ :

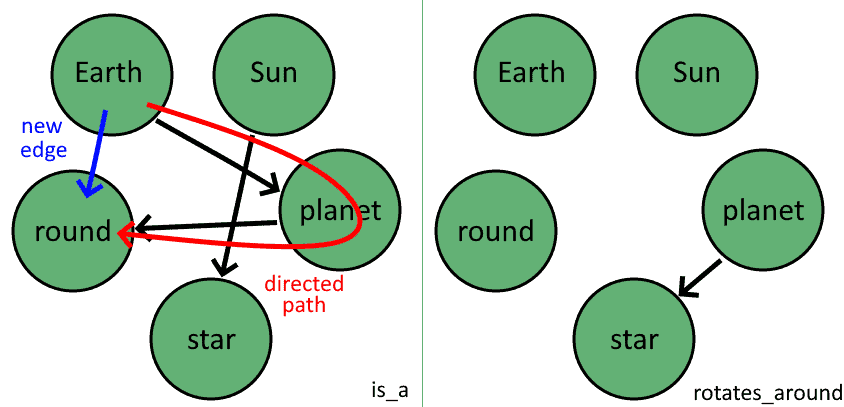
Another way to call this method is forward chaining of the rules. We can apply this method directly on 3-tuples, not necessarily on paths in a graph, with a construction of this form:

Earth is_a planet is_a round $\rightarrow$ Earth is_a round

Remember, the edges of the knowledge graph map to 3-tuples in the Knowledge Base, so it’s always possible to jump from one to the other. In any case, since we just found a new edge between the vertices Earth and round, we can now add a new 3-tuple to our Knowledge Base, which thus consists of 5 elements:

(Earth, planet, is_a)
(Sun, star, is_a)
(planet, star, rotates_around)
(planet, round, is_a)
(Earth, round, is_a)

5.4. Expanding to Multiple Layers

By extending the definition of paths in order to include all edges in the graph, regardless of the layers to which they belong, we can also find trans-dimensional paths. This, in turn, allows us to chain the propositions between layers of the graph:

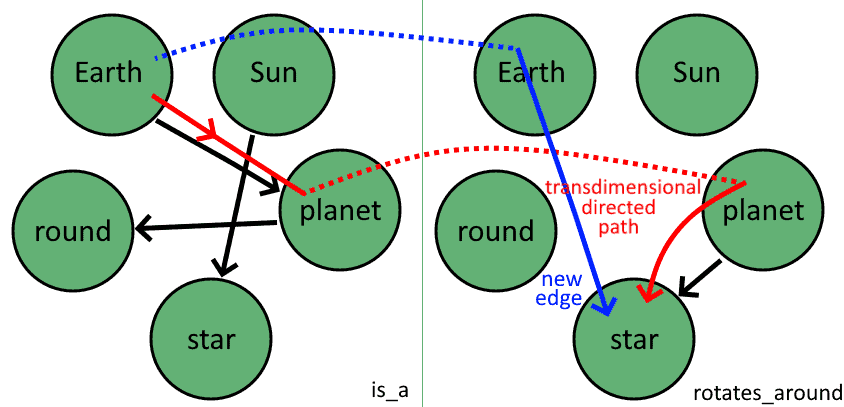
This then allows us to add one more 3-tuple to our Knowledge Base:

(Earth, planet, is_a)
(Sun, star, is_a)
(planet, star, rotates_around)
(planet, round, is_a)
(Earth, round, is_a)
(Earth, star, rotates_around)

Notice finally how this method doesn’t allow us to learn some relationships that don’t correspond to paths in the graph. The 3-tuple (Earth, Sun, rotates_around), for example, is unlearnable through this method, because we can only traverse the graph in the direction of its edges. The method of backward chaining can, in that case, help us evaluate whether that 3-tuple is true, by reasoning recursively through its assumptions.

6. Conclusions

In this article, we studied the theory behind Knowledge Bases, expert systems, and their associated knowledge graphs.

We’ve also seen the procedure for developing a knowledge graph from a set of 3-tuples encoding propositional knowledge.

We’ve finally studied how to perform simple inference by forward chaining of the rules and discussed the relationship between this method for knowledge discovery and paths in graphs.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex