Node Degrees

1. Introduction

In this tutorial, we’ll explain node degrees in a graph.

2. Node Degree

Let be a graph.

The degree of a node is the number of edges with at one end.

If the graph is simple, there can be no more than one edge between any two nodes. In that case, the degree of a node is equal to the number of its neighbors.

For example, the degree of is 4, and the degree of is 5 in this graph since they have 4 and 5 neighbors, respectively:

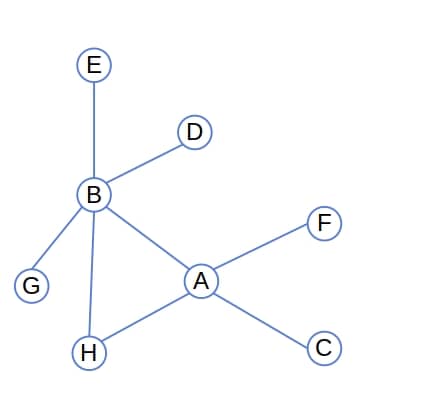
3. Directed Graphs

We differentiate between a node’s indegree and outdegree in a directed graph.

The indegree of a node is the number of edges whose target is . The outdegree of is analogously defined. It’s the number of edges whose source is .

In the example below, the indegree of is 3, and its outdegree is 1:

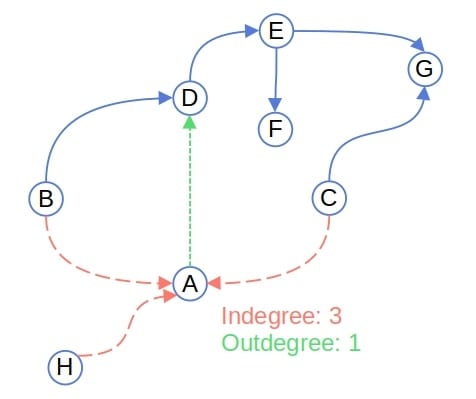
The degree of a node is equal to the sum of its indegree and outdegree. Only nodes in a directed graph have the indegree and outdegree.

4. Degree Distribution

The degree distribution of a graph shows, for each possible degree , the fraction of nodes whose degree is .

Let be the number of nodes whose degree is . The degree distribution is:

where is the total number of nodes in the graph.

This way, we get a probability distribution over natural numbers. We can use it to describe a graph or simulate graphs in numerical experiments.

For example, the distribution of the node degrees in the undirected graph above is:

5. Conclusion

In this article, we explained a node’s degree, indegree, and outdegree.

The degree of a node is the number of edges incident to it. In directed graphs, a node’s indegree is the number of edges directed into it, whereas its outdegree is the number of edges directed out of it.