Yes, we're now running our Black Friday Sale. All Access and Pro are 33% off until 2nd December, 2025:
What Is the Difference Between Labeled and Unlabeled Data?
Last updated: August 30, 2024
1. Overview
In this tutorial, we’ll study the differences and similarities between unlabeled and labeled data under a general-principles approach.
By the end of the tutorial, we’ll be familiar with the theoretical foundations for the distinction between the two classes of data. We’ll also understand when to use one over the other, in relation to the task which we’re solving.
The approach that we’ll discuss here is a bit uncommon. It will however give us a deeper understanding of the relationship between prior knowledge and data collection efforts, and the way that one influences the other.
2. On Data, Information, and Knowledge
We’ll start by discussing a basic idea on how should a generic AI system be built, and see whether from this idea we can derive the necessity to label some of that system’s data. If we can do this, then we can claim that the difference between labeled and unlabeled data doesn’t derive from the specific task we conduct. But rather, that it originates from the Bayesian aprioris of that system’s architecture.
2.1. Conceptual Architecture of Machine Learning Systems
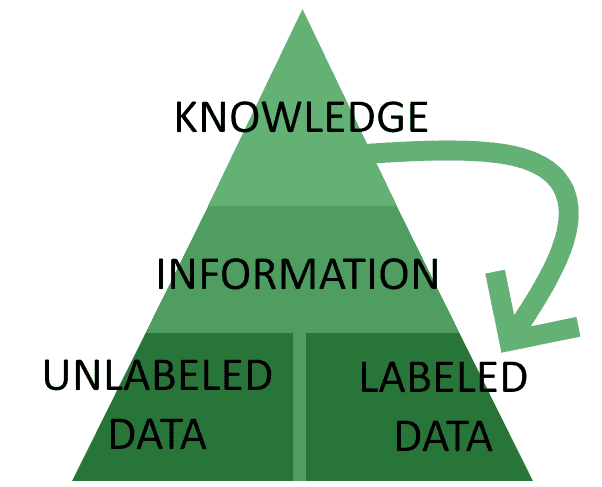
The traditional architecture for the development of AI systems involves the distinction between data, information, and knowledge, and their subsequent arrangement into a hierarchical structure:
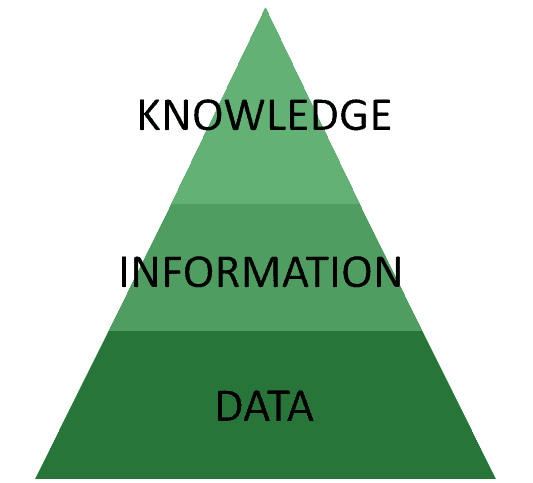
This structure is often called the “knowledge pyramid“ or “DIK pyramid”, where the acronym stands for the first letter of its components. While this theoretical approach has been criticized largely, it’s still generally used as a shared conceptual reference for the development of AI systems.
Within this model, we imagine that an AI system understands the world by aggregating data into information, then processes information to extract knowledge, and then uses that knowledge to direct subsequent data collection.
Let’s now break this model further into its foundational components.
2.2. Data and Measurements
The lowest layer of the pyramid contains the data, which is the ground that connects the machine learning system to reality. We can interpret the data as the collection of measurements or observations performed by sensors, which possess a raw or inarticulated form.
Examples of data are:
- A matrix containing numbers
- Strings of text
- A list of categorical values
- Sampled audio frequencies
Within this context “data” corresponds to the value or values contained in data structures. We’ll see later how to differentiate further into the two classes of data which are the subject of this article.
2.3. Information and the Aggregation of Data
Data can then be aggregated in a number of manners in order to extract patterns from it. Patterns correspond to regularities in the way in which data is distributed, and can be retrieved by imposing mathematical or statistical models on them:
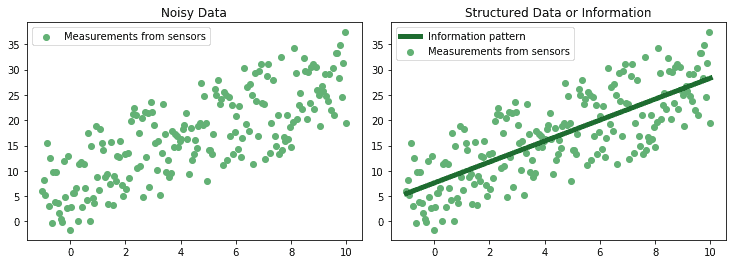
The patterns or schemes corresponding to regularities in the data are often called “information”.
Information has a better capacity to sum-up the complexity in the external reality than the raw data, and this is why we place it at a higher level of the pyramid. Another way to look at the same idea is to say that information, the schemes or patterns of data, allows one to perform predictions on the result of future measurements, while data itself doesn’t.
2.4. On Knowledge and Information
Once patterns have been extracted in a set of data, they can be used to predict the future status of the world, arising from the actions of the system. Say we learn that a certain pattern exists between an object in free fall and its position, as it changes over time:
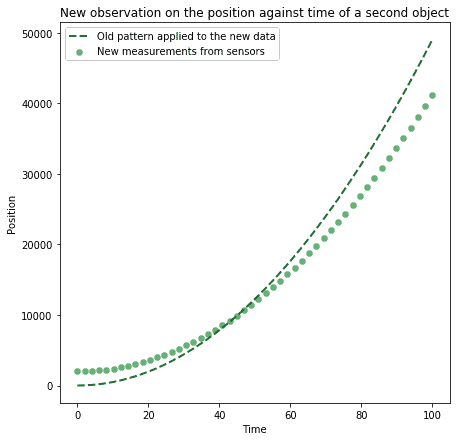
The identification of a suitable pattern for free-falling objects allows us to do two things:
- Predict the future position of a free-falling object
- Push an object and make it fall at an arbitrarily determined speed
We can then generalize the knowledge acquired in extracting this particular pattern to future, unseen situations. After learning that the position over time of free-falling objects changes in a particular manner, we can then generalize this knowledge and assume that, if the position of an object changes over time in a manner corresponding sufficiently well to that pattern, then that object is also free-falling:
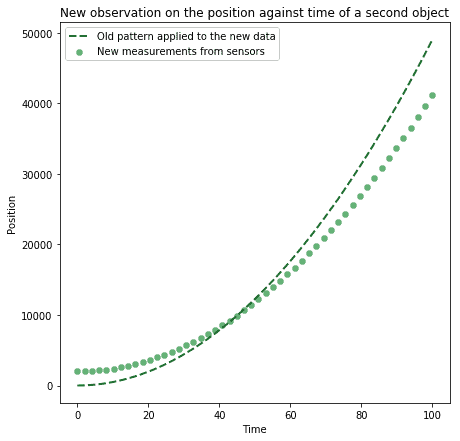
We can lastly group together all data which corresponds to the same class, in the sense that they represent similar real-world phenomena. If we do that, we’re assigning labels to data, which allows us to manipulate it in a predictable and known manner.
2.5. The Relationship Between Knowledge and Labels
In the sense we discussed above, knowledge corresponds to an a priori hypothesis on the way the world functions. This hypothesis, in turn, shapes the expectations we hold regarding measurements that we have or haven’t yet performed.
When we or the machine learning system undertake data collection, we can use that knowledge to aprioristically predict some characteristics of the data we’ll retrieve. Such characteristics derive from the general knowledge we have of the world or the way it functions. In those cases, we can say that we draw from our knowledge certain characteristics that we assume the data to possess.
We can also express this idea in Bayesian terminology. This is done by stating that knowledge on the characteristics of the sensors and measurements corresponds to full confidence that the data collected will have at least some characteristics in common with those collected in other analogous situations. This knowledge then turns unlabeled data, the raw data received by a sensor, into data shaped by an associated prior knowledge:
2.6. Prior Knowledge on Cats and Dogs Turns Unlabeled Into Labeled Data
Say we have two classes of pictures we want to classify with a Convolutional Neural Network. Say also that these classes are “cat” and “dog”. The pictures that we’re showing to the CNN contain the implicit assumption, corresponding to a priori knowledge, that they either belong to the class “cat” or to the class “dog”.
From the perspective of the machine learning system, this assumption can, in other words, be stated as: “In this world, the sensors I possess provide me data which belongs to one of two categories”. The machine learning system, therefore, has prior knowledge or belief that for any given image.
This isn’t necessarily how the world works, but it’s necessarily how the world representation which is implicit in that machine learning system is built. In a sense, and this is the idea we propose in this article, all data is unlabeled data. Only the assignment by us of prior knowledge to it turns that data into labeled data.
3. Labeled and Unlabeled Data
We’ve thus discussed the theoretical foundations for the distinction between labeled and unlabeled data in terms of world knowledge and Bayesian priors. We can now see what technical characteristics do the two categories of data possess. We’ll also learn what machine learning tasks are possible with the one and the other.
3.1. Unlabeled Data
Unlabeled data is, in the sense indicated above, the only pure data that exists. If we switch on a sensor, or if we open our eyes, and know nothing of the environment or the way in which the world operates, we then collect unlabeled data.
The number or the vector
or the matrix
are all examples of unlabeled data. They are unlabeled because from them we don’t understand anything about which sensors collected them, or the status of the world in which they were retrieved. We similarly don’t need to know anything about the way in which that world functions.
In this sense, we have very little or no prior knowledge associated to unlabeled data.
3.2. Labeled Data
Labeled data is data that’s subject to a prior understanding of the way in which the world operates. A human or automatic tagger must use their prior knowledge to impose additional information on the data. This knowledge is however not present in the measurements we perform.
Typical examples of labeled data are:
- A picture of a cat or dog, with an associated label “cat” or “dog”
- A text description for the review of a product, and the score associated by a user for that product
- The features of a house for sale and its selling price
The Bayesian prior that we must use when tagging is sometimes not obvious. We could ask: How can a picture of a cat and the word “cat” be considered as anything but related?

The answer to this question is epistemological in nature and falls outside the scope of this article. In brief, however, we can point to the idea that knowledge held by a system is not necessarily absolute or universal, but it only makes sense in relation to that system. Human taggers need to assign the label of “cat” to an image, drawing from their prior knowledge, in order to assign a label which is otherwise inexistent:

Within this context, labeled data is data on which we superimpose an additional Bayesian prior which isn’t the direct result of a measurement. This prior originates from the knowledge held by a human or machine learning system. This knowledge dictates what the data should be, whether it is or it isn’t.
All the conclusions that we draw on this prior are as valid as the validity of that prior. This is why tagging accurately is a critically important step in the preparation of a dataset.
4. When Do We Use Them
The distinction between labeled and unlabeled data matters. This is because different things that are possible with one aren’t possible with the other. In particular, we can use some machine learning algorithms to work with labeled data and some others with unlabeled data.
According to certain criteria, we’ll end up selecting for our job one type of data over the other. These criteria are:
- the type of task
- the objective of the task
- the availability of the data
- the level of general versus specialized knowledge required to perform the tagging
- the complexity of a decision function
Let’s see them in more detail.
4.1. Types of Task
Labeled data allows the conduct of regression and classification tasks, which fall under the category of supervised learning tasks.
Typical tasks for regression analysis include the prediction of unseen values through multiple or multivariate regression, the identification of a function that maps the relationship between two variables, and the empirical testing of scientific hypotheses
Classification involves the attribution of classes or categories to observations. Machine learning systems perform this attribution on the basis of a list of categories assigned to labeled training data.
Classification is a common task for entity recognition through computer vision and speech-to-text systems. In these systems, we have to identify the label associated with certain input. In doing so, we can learn to recognize objects or words and tag them appropriately:
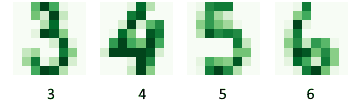
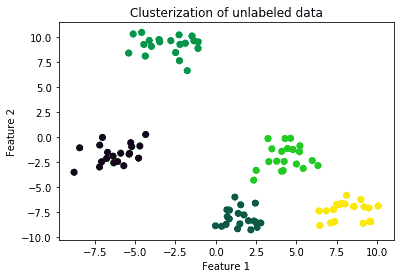
Unlabeled data allows the conduct of clusterization and dimensionality reduction tasks, which fall under the category of unsupervised learning.
Clusterization implies the identification of subsets of observations that share common characteristics, such as being located in close proximity to one another in the vector space to which they belong. Typical clusterization algorithms include K-means, K-NearestNeighbors, and DBSCAN:
Dimensionality reduction tasks are dedicated to the decrease in complexity of a dataset, in order to limit the resources required for its subsequent processing. They include Principal Component Analysis, which is dedicated to the extraction of a simple model from a dataset, and the error which that model has over the original dataset. Other techniques are Autoencoding, Feature Selection, and t-SNE.
Another common task in unsupervised learning is Feature Scaling, which is aimed at standardizing or normalizing a dataset to facilitate the subsequent training of neural networks. This normally takes place as the step immediately prior to feeding data into a neural network, in order to facilitate learning through gradient descent.
4.2. Objectives of the Task
Another criterion according to which we distinguish between the type of data we need is the objective of our work.
Unsupervised learning, and the corresponding unlabeled data used by it, allows the extraction of insights that are purely based on quantitative characteristics of our datasets. Since it requires little prior knowledge, the possible objectives associated with it aren’t normally very complex.
They may involve, for instance, the reduction in the dimensionality of a dataset. Normally we conduct dimensionality reduction for the purpose of limiting the computational resources necessary to train neural networks.
They may also involve the development of a neural network that encodes the dataset into a higher abstract representation. We call this type of neural network “autoencoders”. Autoencoders by themselves have no additional functions, but we can chain them with additional layers for supervised learning.
Supervised learning often has more varied objectives. This is because it presumes a deeper knowledge of the phenomenon which is being studied.
These objectives may include:
- the recognition of objects in images
- the prediction of values of stocks
- the formulation of a medical diagnosis on the basis of x-ray scans
All these objectives imply a relationship between dataset, model, and the external world, which doesn’t limit itself to mathematical abstraction. Instead, it’s based on the understanding that certain characteristics of the world influence certain others. This influence occurs in a stable and predictable way and we can thus use it to operate in the world.
4.3. Availability of Data
The last important criterion involves the availability of tags for data. The labeling of data by human taggers is a very expensive process. It tends in fact to overshadow all other costs associated with the development of a machine learning system.
It’s also time-consuming. Some very well known taggers for images run on very low operational costs, but still require time in order to collect large enough datasets of features and labels.
This implies that the availability of one type of data is often the reason why we chose a certain task. While not impossible, in practice we often don’t select a task in abstract terms, and then start collecting the data. More often, we select the task on the basis of the dataset which we have available. Exceptions to this rule are, of course, frequent.
4.4. General vs Specialized Knowledge of Human Taggers
The availability of labeled data also changes significantly according to whether or not the knowledge encoded in the labels is specialized or general knowledge.
General knowledge is the knowledge that we can realistically expect any human tagger to possess. It includes, for instance, the capacity to recognize between images of cats and dogs, as in the example above. It can also include the capacity to transcript speech in audio or video into text format.
Labeling datasets that require only general knowledge is normally cheap and we can perform it by outsourcing the task to the general population. A typical example of this is the tagging of hand-written digits, which most people can do:
Specialized knowledge is the knowledge that we can expect only an experienced professional to possess.
It includes, for example, the identification of broken bones or dental diseases in an x-ray scan. Only a medical specialist can perform this task and will request a salary that is consistent with their level of professional expertise. For this reason, the labeling of data requiring specialized knowledge has a cost that is proportional to the average salary of a specialist in that sector.
4.5. The Complexity of a Decision Function and the Size of the Labeled Dataset
The costs associated with labeling scale also very poorly as the complexity of the problem increases. The more complex the decision function that a machine learning should learn, the more labeled data the system will require. As a consequence of the increase in the complexity of a decision function, the labeled dataset will need to be larger so that it samples better the decision space:
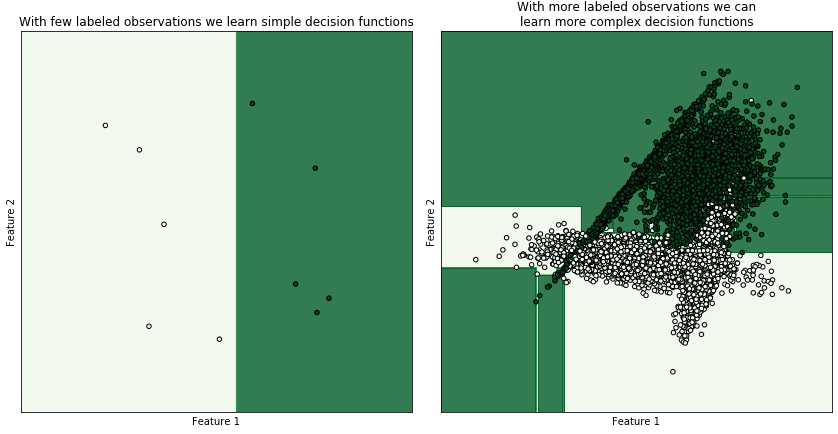
While clusterization might be used to replace classification if the clusters in a dataset are strongly separated, few labeled examples would be required in that case to perform the classification task, thus invalidating the condition discussed in this paragraph.
5. Conclusions
In this article, we’ve studied a Bayesian and information-theoretic explanation of the difference between labeled and unlabeled data.
First, we suggested considering all data originating from sensors or measurements as generally unlabeled. If we do so, we can then treat labeled data as unlabeled data to which we add prior knowledge on its structure or function.
We’ve also seen how we can derive the distinction between labeled and unlabeled data from basic principles of the architecture of machine learning systems. Labeled data is data that is shaped by assumptions on the way in which the world functions.
We’ve finally seen the criteria according to which we select one over the other. These, in particular, are the type and objective of the task, and the availability of labeled data.