1. Overview
Machine learning algorithms look at the input as numbers only, without thought to scale or units.
Unless programmed differently, they won’t understand the scale; they’ll assume that larger values should be given greater weight.
To avoid issues with this assumption, we can use Feature Scaling.
2. What Is Feature Scaling?
Feature Scaling involves modifying values by one of two primary methods: Normalization or Standardization. Normalization takes the input values and modifies them to lie between 0 and 1. Standardization methods modify the values so that they center at 0 and have a standard deviation of 1.
There are many variations to these methods, which we’ll discuss below.
3. Why Should We Use Feature Scaling?
As mentioned above, machine learning algorithms may assume that larger values have more significance.
For example, let’s consider car data. Engine displacements may range in the hundreds. Miles per gallon values are normally less than 100.
A machine learning algorithm might think that the engine displacement is more significant in our problem. Engine displacement then might play a more decisive role when training our model.
Another reason to scale our values may have to do with how fast a model will converge. A Neural Network Gradient Descent model will converge much more quickly with feature scaling than without.
4. When Should We Use Feature Scaling?
As a rule of thumb, we should always use feature scaling when we are working with an algorithm that calculates distances between points.
Principal Component Analysis (PCA) is a prime example of an algorithm that benefits when numeric values are scaled. If the values are not scaled, the PCA algorithm may determine that the changes in the smaller values are much more important than changes in the larger ones.
Other algorithms that can benefit from feature scaling include:
- Support Vector Machine (SVM)
- K-nearest neighbor
- Logistic Regression
- K-Means Clustering
For example, we can use the urine dataset in the R boot library and the SVM algorithm:
svmfit.poly.noscale = svm(r ~ ., data = urine, kernel = "polynomial", cost = 7, scale = FALSE)
And we’ll see the following output when we run it:
WARNING: reaching max number of iterationsIn addition, the algorithm has a hard time separating the samples:
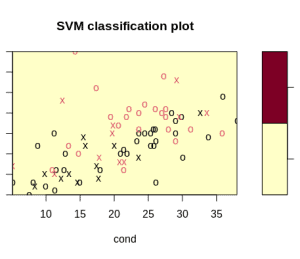
Adding feature scaling improves our output and the algorithm calculations:
svmfit.poly.scale = svm(r ~ ., data = urine, kernel = "polynomial", cost = 7, scale = TRUE)This time, there is no warning message, and the algorithm begins to see a delineation:
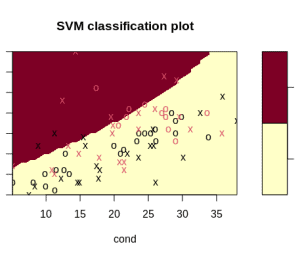
Not all values need to be feature scaled. For example, ordinal values would not benefit from feature scaling. But continuous values do. Continuous values can be modified without affecting the covariance matrix.
Scaling is not necessary in all instances. If we’re going to be using our data in a tree-based algorithm, there’s no advantage to scaling.
If time and resources allow, we can try our machine learning models with raw data, standardized data, and normalized data to see if there is any benefit to scaling our values.
Now, let’s explore ways that we can achieve feature scaling.
5. Performing Feature Scaling
We can use several methods to perform feature scaling. Most are based upon one of two principles:
- modifying the values so that they all lie between 0 and 1
- modifying the values so that they center on 0
The primary methods used are:
- Min-Max
- Standardization
Variations on these include:
- Max Abs
- Robust
- Quantile Transformer
- Power Transformer
- Unit Vector
5.1. Min-Max
In the Min-Max scaler, or Normalization, we transform the values so that they lie within a given range. This scaler is a good choice for us to use if the standard deviation is small and when a distribution is not Gaussian. This scaler is sensitive to outliers.
The formula typically used for Min-Max Scaling is:
5.2. Standardization
Standardization, or Z-score normalization, assumes that the data is normally distributed. It scales them so that they center around 0 and have a standard deviation of 1. This is accomplished by subtracting the mean value:
where 
(the mean) is:
and 
(standard deviation) is:
Standardization assumes that our data follows a Gaussian distribution. This is not a good choice if our data is not normally distributed.
5.3. Max Abs
The Max Abs scaler scales and translates the values so that the maximum absolute value is 1.0. It doesn’t shift or center the data, so it doesn’t destroy any sparsity.
This scaler is sensitive to outliers if all the values are positive.
5.4. Robust
The Robust scaler removes the median, then scales the data to lie within the Interquartile Range — between the 1st quartile (25%) and the 3rd quartile (75%). This scaler is not influenced by a few large marginal outliers since it’s based on percentiles.
5.5. Quantile Transformer
This scaler – also called the Rank Scaler – employs an Inverse Normal Transformation. It transforms the values to follow a normal distribution. This transformation tends to spread out the most frequent values. It also reduces the impact of marginal outliers.
5.6. Power Transformer
The Power Transformer scaler transforms the data to make it more Gaussian. This algorithm is useful when there are issues with the variability of the data or situations where normality is desired.
5.7. Unit Vector
The Unit Vector Transformer considers the whole vector to be of unit length. Like Min-Max Scaling, this algorithm produces values between 0 and 1. This algorithm is quite useful when dealing with boundaries, such as image values where the colors must be between 0 and 255.
6. Conclusion
Data Transformation is an important step for our Machine Learning Preprocessing. We can improve our results and often speed up our processing by modifying our data so that it fits within normal bounds.
Check out these from our growing list of Machine Learning articles: