PCA: Principal Component Analysis | Baeldung on Computer Science

1. Introduction

As the name suggests, principal component analysis (PCA) finds the principal aspects of a model.

In this tutorial, we’ll present PCA on three different levels. First, what kind of answers and information does PCA give us, and how can we use them? Second, we’ll give an outline of how to program PCA and the algorithms needed to perform it. And third, we’ll explore a little more in-depth the intuition and techniques behind the PCA method.

2. PCA Overview

Suppose we have a lot of data consisting of a lot of parameters that describe something in our model. Intuitively, we know that some parameters can contribute to a problem and some have absolutely no effect.

For example, in predicting the weather, the day of the week probably has no significance, but the date could have significance. However, maybe a better parameter could be the month or even the season. Of course, we have other parameters such as temperature, pressure, wind direction, the weather yesterday, and others.

The bottom line is that we have a lot of parameters to choose from. Intuitively we choose the “reasonable” ones. But, a better approach is to have a method that quantitatively chooses the best for us.

This is where principal component analysis comes into play. It’s a quantitative method that can be used to find the best parameters to describe our system.

3. Occam’s Razor, PCA, and a Simple Model

The principle of Occam’s Razor is simplicity. In terms of modeling, the principle of Occam’s razor asks why we should use a complex model when a simple model will suffice.

This is exactly what PCA promotes. It helps us find a set of coordinates that are “good enough” to explain the data we are modeling.

The principle of simplicity is not only aesthetically desirable, but it can also have advantages in data analysis. Focusing on key parameters, such as those provided by PCA, within almost any data analysis technique will improve its efficiency and the quality of the result. Including parameters that do not contribute to the model’s behavior just makes the computation less efficient, and other parameters just contribute noise to the problem.

Let’s take a closer look at what all of this means.

4. The Principal Component

What do we mean by the principal component? Let’s take an example of two-dimensional data:

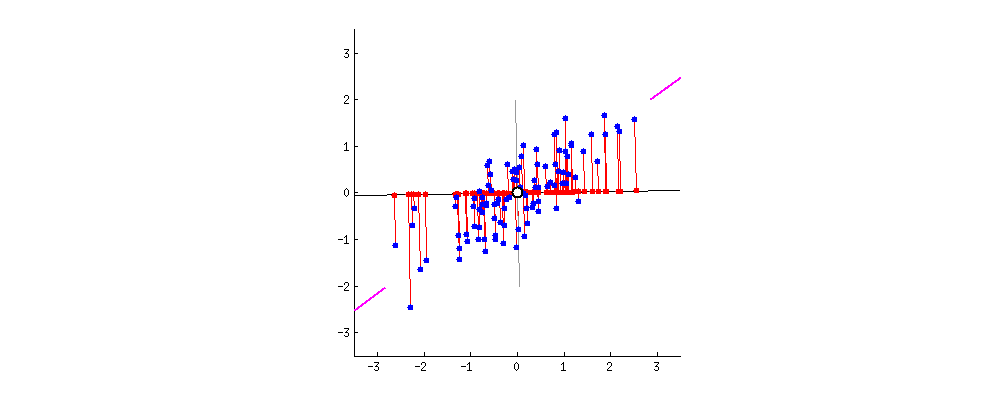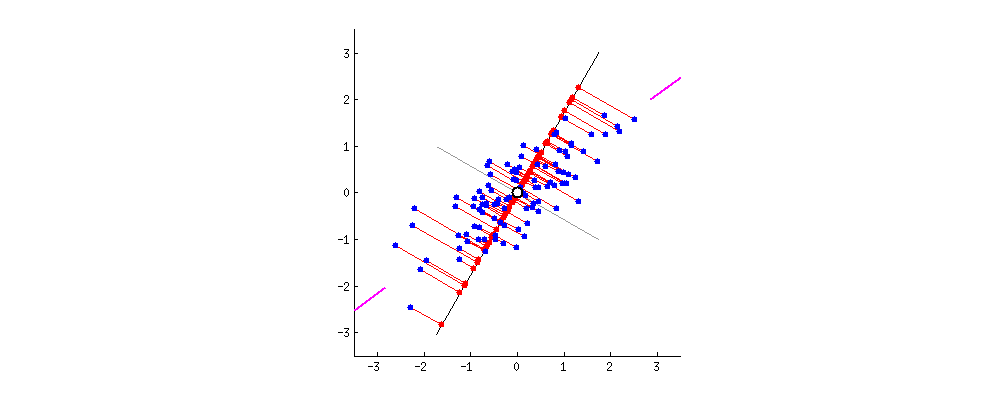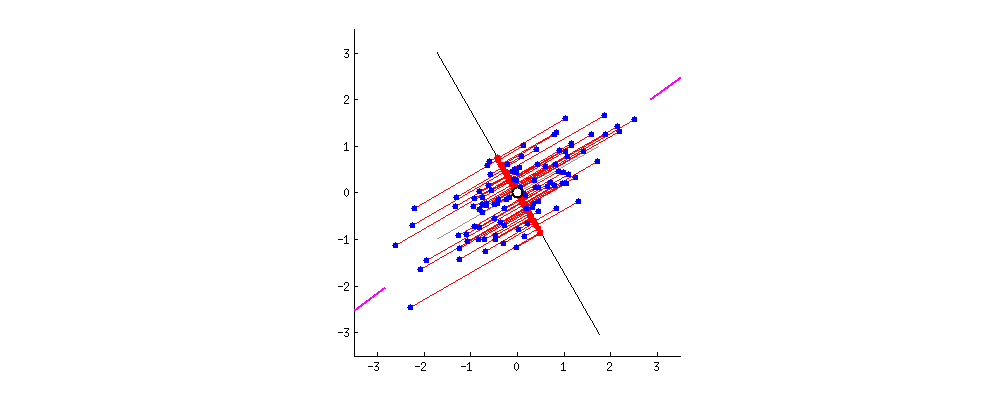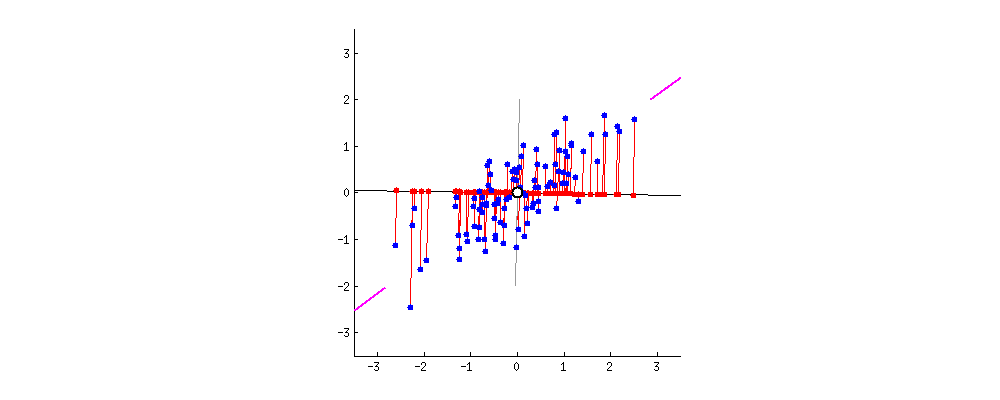
Intuitively, looking at the graph, we see that the collection of points is sort of an oblong shape. This means that the x and y coordinates that we have are somewhat related. As x increases in value, for the most part (a key phrase), the y values increase.

We can see how related the two coordinates are by drawing a line through the oblong shape of points. This would be the principal component. So, qualitatively, we can say that y increases with x. We can add, quantitatively, that this increase is with the slope of the principal component.

4.1. Is the Principal Component Sufficient?

We can then ask the quantitative question, “Is the principal component sufficient?”. The component perpendicular to the principal component (or orthogonal in the language of linear algebra) gives us the error that would arise if we were to just describe the relationship with just the principal component.

Suppose our answer is: “Yes, the principal component is sufficient”. Then we’ve created a simpler model with only one parameter instead of two. This would make Occam happy. But, in addition, we have a quantitative estimate of the error we could expect if we were to use this relationship.

For example, we could take the average of the absolute values of the errors. For example, the perpendicular coordinate gives the error. But, the principal component analysis also gives parameters that indicate how well the components describe the entire space.

Suppose our answer is “No, the principal component is not sufficient”. Here, at least, we have specific, quantitative criteria, meaning the errors in the principal component, as to why we chose to keep two parameters.

4.2. How Did We Find the Principal Component?

We can see from the graphic above that first we find the middle of the set of points. This is the mean of both coordinates. We use that as our origin of our new coordinate system. Next, we rotate these new coordinates until the error, represented by the red lines drawn from the principal component, is minimized.

When the principal component goes through the middle of the long side of the oblong set of points, the errors are minimized and we have found the position of the principal component.

4.3. A New Coordinate System

As we have seen from the above, the result of PCA – that is, finding the principal component – involves finding a new rotated coordinate system centered around the mean of the data points. In a two dimensional example, the new x-axis is rotated along the principal axis of the points, meaning the ‘best’ straight line drawn through the set of points:

We see from this graph, the exact coordinate of each point can be represented either in the original x and y coordinates or the same point can be represented in the rotated x and y coordinates. We can say that the point is the same, but the numbers used to say where the point changes depending upon which reference we use — the original coordinate system, or the new coordinate system.

4.4. Rotation of Coordinates

When we rotate from one coordinate system to another, there is an exact transformation between the two. No information is lost, just the two numbers representing the coordinates change.

Let us take a two-dimensional example again, where the y coordinate grows almost at the same rate as the x coordinate. This means that the principal component is at a 45-degree angle to the original coordinates (think of a right triangle: the two perpendicular sides are equal and the angle is 45 degrees).

Now we can rotate the graph so the new coordinates lie horizontally and the old coordinates are tilted:

We see here, once again, that we have lost no information. If we look at the points in the original graph, we see that the x and y values are exactly or almost the same, like the point (1,1). This means that the x and y coordinates are correlated.

However, if we rotate the coordinate system, we have a new coordinate system. In this coordinate system, the x value can be large, but the y value is zero or close to zero. For example, the point (1,1) in the original system is (√2, 0.0) in the new (later we will see how this was calculated).

4.5. The Result: PCA Component Vectors

The result of the PCA algorithm, is a set of orthogonal (perpendicular in 2-D space) unit vectors, pointing along each component.

In the diagram, these are vectors pointing along the blue lines. Each component is a unit vector, meaning its length is one. If we set up the set of PCA component unit vectors as rows in a matrix, T, we have the transformation matrix for converting the original coordinates into the new coordinates.

In our two dimensional example above, the PCA algorithm gave us two unit vectors:

$\begin{equation*} (\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}), \; \; (-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}) \end{equation*}$

The first points along the direction of the principal component, and the second points along the perpendicular to the principal component.

If we set these two vectors as rows in a matrix, then we have the transformation matrix. Multiplying the transformation matrix by the original coordinates produces the same point in the new coordinates:

$\begin{equation*} T \begin{pmatrix} x\\ y \end{pmatrix} = \begin{pmatrix} \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\\ -\frac{\sqrt{2}} {2}& \frac{\sqrt{2}}{2} \end{pmatrix} \begin{pmatrix} x\\ y \end{pmatrix} = \begin{pmatrix} x \frac{\sqrt{2}}{2} + y \frac{\sqrt{2}}{2}\\ - x \frac{\sqrt{2}}{2} + y \frac{\sqrt{2}}{2} \end{pmatrix} \end{equation*}$

Later we will see more on how this transformation matrix was formed.

4.6. Dimension Reduction

How can we use these PCA component unit vectors to reduce the dimension of our problem?

Using PCA in n-dimensional space will result in another set of component unit vectors in the ‘optimized’ rotated coordinates also in n-dimensional space. But associated with each PCA component vector, v_i, is a value, λ_i, giving a quantitative indication of how much that component explains the set of data.

The first principal component has the highest λ value. If that’s good enough to describe our data, such as in our example, we can then say we have reduced the problem from an n-dimensional to a 1-dimensional problem.

However, if that’s not enough, we can successively add additional components, each with successively lower λ values, until we think that the resulting set of m components is good enough to describe our system. In this way, we have reduced our system from an n-dimensional system to an m-dimensional system, where m < n.

Although the above, more intuitive method would work, can we do this so we have a quantitative indication of how much we have described the data? Fortunately, the answer is “yes”. The PCA component λ values associated with each PCA vector component gives a quantitative measure of how important that component vector is.

If we consider that all the vectors describe exactly all the data, the total sum of the PCA component λ values represents 100% of the data set. To determine how much of the data a particular component explains, we need only divide it by the total:

$\begin{equation*} portion \: of \: data \: explained \: by \: component \: i \:= \: \frac{\lambda_{i}}{\Sigma_j^{n}\lambda_j} \end{equation*}$

So if we order the component values, λ, from highest to lowest, the portion of data described by the first m components is:

$\begin{equation*} portion \: of \: data \: explained \: = \: \frac{\Sigma_k^{m}\lambda_k}{\Sigma_j^{n}\lambda_j} \end{equation*}$

This sum is a quantitative measure, with 1.0 being that the data is 100% described, of how good our reduced dimensional space is.

5. Computing the PCA

There are basically four steps to computing the principal component analysis algorithm:

Set up the data in a matrix, with each row being an object and the columns are the parameter values – there can be no missing data
Compute the covariance matrix from the data matrix
Compute the eigenvalues and eigenvectors of the covariance matrix
Use the eigenvalues to reduce the dimension of the data

Other than the core step, computing the eigenvectors and eigenvalues, the algorithm is relatively simple to program. But fortunately, most programming languages would include a numerical routine for computing the eigenvectors and eigenvalues.

In the next section, we give more detail about the steps in the PCA algorithm.

5.1. Data as a Matrix

PCA helps find an optimal representation of data stemming from a set of objects.

In order to use PCA, each object in the data needs to be represented by a set of numerical descriptive parameters. Typical examples of this type of representation can be found in some standard test data set for machine learning (for some examples, see the UCI Machine Learning Repository or Kaggle).

When we order the set of parameters, the corresponding numerical values for each object can be put in a vector. For example, in the Iris dataset from the UCI Machine Learning Repository, there are five attributes:

sepal length in cm
sepal width in cm
petal length in cm
petal width in cm
class (Setos, Versicolour, Virginica)

We see that the first four are numerical attributes and can be directly used. But, also see that the fifth class is one of three, non-numeric classes. However, we can easily resolve this by assigning a number to each class:

Setosa
Versicolour
Virginica

Now, we can represent each iris object in the dataset with a vector — for example, the first object in the dataset is:

5.1, 3.5, 1.4, 0.2, 1

The dataset consists of 150 objects, 50 from each class (attribute 5). If we put each object vector as a row in the dataset matrix, we have finally a matrix with five columns, corresponding to the attributes, and 150 rows, corresponding to each data object. This graphic summarizes the process:

We should also note that the data needed for the PCA has to be adjusted relative to the mean values of each column. In our data, the respective means of the parameters are:

5.84, 3.05 , 3.76 , 1.20, 2

This means our first object will have the values:

-0.74, 0.45, 2.36, -1, -1

In the algorithm in the next section, this adjustment is taken as part of the algorithm.

5.2. Programming Overview

In order to program the PCA method, we’ll need a set of numerical routines. The simpler can be easily programmed and the more complex can be found in standard packages or libraries. We list them here as pseudo functions that will be used in the PCA pseudo-code:

FormDataAsMatrix(original, matrix): Form the data matrix from the original data structure (depending on programming language and data). Each row of the matrix is the vector of each data point.
AdjustMatrixToMean(A): The mean of the columns is found, and the column values are adjusted to the mean. This means that we should subtract the column mean from each column value. This adjustment is a requirement of the PCA algorithm.
Mult(A, B, C): Multiply matrix A (m rows by k columns) with matrix B (k rows by n columns) by putting the result in C (m rows by n columns).
TransposeMatrix(A, T): Transpose the matrix A (m rows by n columns) and put result in T (n rows by m columns).
EigenvectorsAndEigenvalues(A, E, V): Given a square matrix A (n rows and n columns), compute the n eigenvectors and respective eigenvalues and put them in matrix E (n rows and n columns) and vector V (n values), respectively. This is the heart of the PCA algorithm.

5.3. The PCA Algorithm

The PCA algorithm is basically a sequence of operations (no loops or optimizations) using the functions listed in the previous section. The algorithm shown takes as input the modeling data in some representation. This could be a data structure, such as a class in Java or C++, or a struct, for example, in C.

The critical steps of the algorithm are the creation of the correlation matrix between the parameters and then finding the eigenvectors and eigenvalues of this matrix.

The algorithm listed here returns as output a set of new coordinates. Using the eigenvalue information, only the ‘essential’ coordinates are given in the final matrix.

The size of the full eigenvalue matrix is n by n, where n is the number of parameters. The size of the final matrix is m rows, where k is less than m:

6. Principles Behind the Method

6.1. Vector Basis Sets

The core of the PCA algorithm involves the transformation of coordinates. This is a fundamental principle of linear algebra where same vector can be represented as different linear combinations of different fundamental vectors, different basis vectors. The number of basis vectors that are needed determines the dimension of the vector system.

In the original coordinate system used in our original example, the basis vectors are:

(1) $\begin{equation*} (1,0),\;\; (0,1) \end{equation*}$

Thus a point on the graph, such as (2,2) can be represented as a linear combination of these two points:

$\begin{equation*} $(2,2) = 2 ^{.} (1,0) + 2 ^{.} (0,1) \end{equation*}$

The vector pointing to (2,2) is found by going two times the direction (1,0) and two times the direction (0,1):

When we rotate the coordinate system 45 degrees as we did in our initial example, the basis vectors change. In the rotated system, we still need two vectors, but now they are:

$\begin{equation*} (\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}), \; \; (-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}) \end{equation*}$

Thus the point (2,2) in the original coordinates are, in the new coordinates:

$\begin{equation*} (2\sqrt{2}, \; \; 0) \end{equation*}$

because, when multiplied by the basis vectors:

$\begin{equation*} (2\sqrt{2}) \;^{.}\; (\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}) + \; (0) \;^{.}\; (-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}) \end{equation*}$

In this graph we see the basis vectors in thick lines and how the original point, (2,2), is transformed:

6.2. Dimensionality Reduction

In the previous section, we saw that a coordinate in n-dimensional space (the example was where n was 2) can be represented in different ways with different basis vectors. In the original space or the transformed space, we still need n vectors (2, in the example) to exactly describe all the space.

However, what if we have the special case where all the points in the space fall along a line, for example:

We can describe all points with a single parameter, c, and a single vector, (1,1):

$\begin{equation*} (x,y) = c ^{.} (1,1) \end{equation*}$

In this case, we don’t need the second vector for any of the points. Even though the line is drawn in two-dimensional space, the information can be described in a one-dimensional space. In our example, this is a single vector such as (1,1). Or if we rotate the coordinate system, we can draw the points in one-dimensional space:

This example shows the process of dimension reduction in going from two dimensions to a single dimension. The purpose of PCA is to find this optimal set of reduced coordinates.

If we look again at the initial example, we see the reduction of the two-dimensional space to one-dimensional space:

The perpendicular coordinate to the principal component can be viewed as the error to expect when only using one dimension.

6.3. A Bit of Geometry and Coordinate Projection

These component unit vectors are used to find the transformation of the old coordinates to the new rotated coordinates. This is done by projecting the old coordinate onto the new. In other words, if we move to point x in the original direction, how far along the new axis do we move:

Mathematically speaking, a projection of one vector on the other is the dot product of the two vectors.

This diagram gives three cases of the dot product projection, exactly, somewhat and not correlated:

The first is where the vectors are the same and the dot product is 1.0. The last one, where the vectors are orthogonal (perpendicular), there is no projection of one to the other, so the dot product is zero. And the one in the middle is half-way between.

6.4. The Transformation Matrix

The set of PCA component unit vectors that are a result of the PCA algorithm make up the transformation matrix.

The hypotenuse of the right triangle is the projection of the original coordinates and becomes the new x’ coordinate. There is no y’ component, so it’s zero.

Using these arguments, when we rotate the coordinates by θ, which in our case is -45 degrees (we are rotating clockwise), we can create a general transformation matrix, T, from the original coordinates (x,y) to the rotated coordinates (x’,y’):

$\begin{equation*} T = \begin{pmatrix} cos( \theta) & - sin( \theta) \\ sin( \theta) & cos( \theta) \end{pmatrix} \end{equation*}$

$\begin{equation*} \theta = -45^{\circ} = \frac{\pi}{4} \end{equation*}$

$\begin{equation*} T = \begin{pmatrix} \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\\ -\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{pmatrix} \end{equation*}$

This transformation matrix is exactly what would’ve resulted from performing PCA on this example.

By multiplying this transformation matrix by the original coordinates, we get the new coordinates:

Thus to get the new coordinates of, for example (1,1), we need only to multiply by the transformation matrix:

$\begin{equation*} \begin{pmatrix} \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2}\\ -\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{pmatrix} \begin{pmatrix} 1.0\\ 1.0 \end{pmatrix} = \begin{pmatrix} (1.0) (\frac{\sqrt{2}}{2} )+ (1.0 )(\frac{\sqrt{2}}{2})\\ (1.0)( -\frac{\sqrt{2}}{2}) + (1.0) \frac{\sqrt{2}}{2}} \end{pmatrix} = \begin{pmatrix} \sqrt{2}\\ 0 \end{pmatrix} \end{equation*}$

But where did numbers like √2/2 within the vectors come from? To quantitatively understand this, it helps to look at some very simple triangles. We can see how the projection of the old coordinate onto the new coordinate is formed.

We start by noting that the rotated principal coordinate is at an angle θ relative to the original coordinates. The length of the new coordinate, x’, relative to the original, x, is through the cosine function, namely, x´= x/cos(θ).

We see that in our special case where θ is 45 degrees, the coordinate (1,1) gets get translated to:

$\begin{equation*} (\frac{\sqrt{2}}{2}, 0) \end{equation*}$

6.5. Covariance Matrix

The variance of a single parameter is a measure of the spread of values of that parameter. The variance of a set of N parameters, X_i, is calculated using:

Var(X) = Σ ( X_i – m_x )² / N

where m_x is the mean of all the values, X_i.

The covariance of two parameters measures the extent the two parameters move together. How together are the spread of points? To calculate the covariance between two variables X and Y, we use the formula:

Cov(X, Y) = Σ ( X_i – m_x ) ( Y_i – m_y ) / N

Intuitively, we can see why covariance is important for the PCA method. The goal of PCA is to group together sets of variables that move together. In other words, if they have a large covariance value, then they should be in the same component.

If we want to collect all the combinations of covariances between all the parameters, then we form the covariance matrix. Each element, c_ij, of the covariance matrix gives the covariance between X_i and X_j.

Using matrices, it’s very easy to calculate the covariance matrix. There are basically three steps:

Calculate the mean, m_j, of each parameter j for all N objects, i: m_j = (∑_i x_ij)/N
Subtract this mean from the corresponding parameter, j, for each object, i, to form a mean adjusted data matrix, A: a_ij=x_ij-m_j.
Calculate the covariance matrix, V, by multiplying the transpose of A by itself, V=A^TA.

The PCA method determines the set of components by finding the eigenvectors and eigenvalues of the covariance matrix V.

6.6. Eigenvalues and Eigenvectors

Computing the eigenvalues and eigenvectors of the covariance matrix is the key to finding the principal components of a set of data.

When we transform a given vector x with an arbitrary transformation matrix M, normally we get another vector y which is pointing in a different direction. However, there is a set of vectors, x_i, such that when multiplied by M, the vector is only scaled by a factor λ_i:

M x = λx

We see that instead of resulting in a vector y pointing in another direction, the result is in the same direction, x_i, but just scaled by the parameter λ_i.

What about a transformation of an arbitrary vector, y? We can represent the vector y in terms of the set of eigenvalues, x_i, because the eigenvectors just represent a different basis:

y = ∑_i a_i x_i

So, when we do the transformation, we get a new linear combination of eigenvectors:

M y = M(∑_i a_i x_i)
= ∑_i M (a_i x_i) = ∑_i a_i M x_i
= ∑_i a_i λ_i x_i

Now, as we saw earlier, the size of the eigenvalue reflects the strength of the eigenvector in explaining the data. Since each term in the sum is multiplied by the eigenvalue, the contribution of that term is dependent on the strength of the eigenvector.

So, terms with small eigenvalues will not contribute as much to the vector y and thus, if small enough, can be ignored.

7. Conclusion

In this tutorial, we’ve seen the essentials of principal component analysis (PCA) explained on three basic levels.

First, we outlined why PCA is useful in understanding data and how it can be used in reducing the dimensionality of the data. Then, we described the basics of how to program PCA. Finally, we went into further depth into the essential concepts behind PCA.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex