Differences Between Luong Attention and Bahdanau Attention

1. Introduction

Attention is a mechanism used in artificial intelligence and machine learning that dynamically highlights the most important and relevant parts of the data input. It has been shown to have a great impact on the overall performance of deep learning models.

In this tutorial, we’ll introduce two widely used attention mechanisms, the Luong and Bahdanau attention. We’ll discuss their different techniques, analyze their different mathematical approach, and walk through their benefits and limitations, along with some common applications and usages.

2. What Is Attention Mechanism?

The attention mechanism is widely used in natural language processing tasks where the input consists of long sequences of words. The idea behind this technique is that the neural network “pays attention” to certain components of the input and ignores less relevant parts of it.

When translating a statement from one language to another, for instance, the attention mechanism may focus on specific words in the source phrase while ignoring others better to comprehend the context and meaning of the total phrase.

Thus, this approach focuses on certain input sections by first encoding them into a group of hidden states and then determining a series of attention weights. These attention weights define the relevance of each hidden state in generating the output. The outputs are then formed by summing the hidden states and weighting them according to the generated attention weights.

For example, suppose we have a sentence that we would like to translate. The attention mechanism maps the importance of each word with a certain weight and assigns higher values to the most significant ones: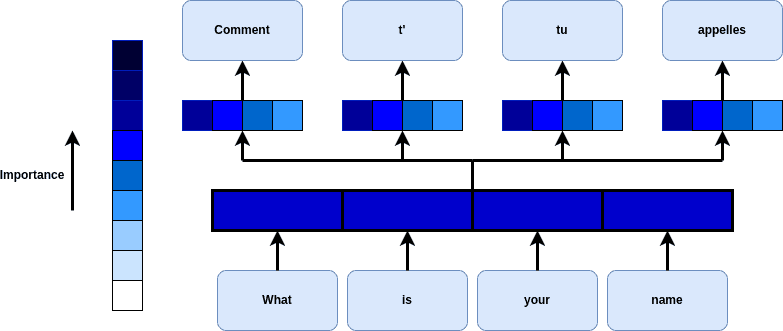

These techniques improve the model’s capacity to handle extended input sequences and resolve the problem of vanishing gradients.

3. Luong Attention

Luong attention, also known as scaled dot-product attention, is a type of attention mechanism introduced by Minh-Thang Luong in the paper “Effective Approaches to Attention-based Neural Machine Translation” (2015). It is frequently employed alongside recurrent neural networks (RNNs), such as long short-term memory (LSTM) networks.

This technique’s attention weights are generated by employing a set of standard scoring algorithms that use as input the decoder‘s actual hidden state and the encoder‘s hidden states as well. These algorithms yield a score that indicates each encoder state’s “impact” in creating the current decoder state. Therefore, the produced scores are then used to compute the attention weights.

3.1. Luong Attention Mechanisms

The Luong attention mechanism comes in various forms, each with a unique scoring function. Dot-product attention, general dot-product attention, and concatenation attention are typical instances.

General attention computes the dot product between the attention matrix and the current hidden state, which results in a single scalar:

(1)  

Concatenation attention concatenates the current hidden state with each encoder hidden state and applies a feed-forward neural network to compute the attention scores:

(2)  

Dot attention is the simplest form, which computes the dot product between the current hidden state and each encoder hidden state, which results in attention scores:

(3)  

Where is a matrix containing the hidden states of the encoder, is the current hidden state of the decoder, and are learned parameters, and [;] represents the concatenation of vectors.

As we can see, after the computation of the dot product between a fixed set of learned parameters, called the attention matrix, along with the encoder/decoder states, a softmax function is applied to the dot result to obtain the attention weights.

4. Bahdanau Attention

Bahdanau attention, also known as Additive attention, is a type of attention mechanism that was first introduced by D. Bahdanau, K. Cho, and Y. Bengio in their paper “Neural Machine Translation by Jointly Learning to Align and Translate” in 2015.

Unlike the Luong attention case, the authors of the paper propose a more complex way than just using a mathematical approach to compute the attention weights by conducting a linear combination of encoder and decoder states. Bahdanau technique employs and trains a feed-forward neural network. Moreover, the current state of the decoder, the previous state of the attention mechanism, and the current input are driven through the neural network.

Next, the attention weights are utilized to produce the weighted sum of the features of the input. This weighted sum is provided as additional information to the decoder, allowing it to focus on important input factors when producing a single output.

4.1. Mathematical Approach

Specifically, the attention weights are calculated using the following equation:

(4)  

Where is a matrix containing the hidden states of the encoder, is the current hidden state of the decoder, , , , and are learned parameters, and is the hyperbolic tangent function.

Bahdanau attention can learn more complex relations between the data than other types of attention mechanisms because it employs a neural network to compute the attention weights rather than a simple mathematical algorithm. It is also a powerful technique as it allows the attention weights to be learned directly from the data.

5. Differences Between Luong and Bahdanau

Luong and Bahdanau’s attentions share the main idea but use a different approach to achieve it. First of all, for the computation of the attention weights, Bahdanau attention uses a neural network, while Luong attention uses a more simple and straightforward mathematical approach. Therefore Bahdanau includes many more parameters than Luong attention, which may lead to overfitting if the training data is not large enough and is computationally more expensive as it involves training a neural network. 

Lastly, during the computation of the weights, Bahdanau uses the previous attention state and current decoder state. On the other hand, Luong utilizes only the current decoder state to compute attention weights.

6. Advantages and Disadvantages

Luong and Bahdanau’s attentions have their own benefits and limitations, and the choice of which to employ depends on the specific task and the application requirements. A summary of their main advantages and disadvantages is shown in the table below:

7. Applications

In general, attention mechanisms are used in Natural Language Processing (NLP) and Computer Vision tasks such as speech recognition, machine translation, and text summarization. They have also been used in Recommendation Systems to make better suggestions.

Bahdanau attention is particularly useful in Neural Machine Translation (NMT) tasks because it has the ability to handle longer input sequences, and it explicitly models the alignment between the input and output sequences, which can lead to more accurate translations. Both attention mechanisms are commonly used in NLP tasks like dialogue systems and conversation modeling.

8. Conclusion

In this tutorial, we walked through the attention mechanism. Specifically, we talked about the Luong and Bahdanau attention methods. We introduced their different technique in their effort to achieve concentration on a specific part of the input, analyzed their mathematical approach, and discussed their main differences. We also discussed their advantages and disadvantages and mentioned common applications in which attention mechanisms can be employed.