Learn through the super-clean Baeldung Pro experience:
>> Membership and Baeldung Pro.
No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.
Last updated: February 13, 2025
In this tutorial, we’ll talk about the sigmoid and the tanh activation functions. First, we’ll briefly introduce activation functions, then present these two important functions, compare them and provide a detailed example.
Finally, we’ll provide the implementation details of the sigmoid and the tanh activation functions in Python.
An essential building block of a neural network is the activation function that decides whether a neuron will be activated or not. Specifically, the value of a neuron in a feedforward neural network is calculated as follows:
where are the input features,
are the weights, and
is the bias of the neuron. Then, an activation function
is applied at the value of every neuron and decides whether the neuron is active or not:
In the figure below, we can see diagrammatically how an activation function works:
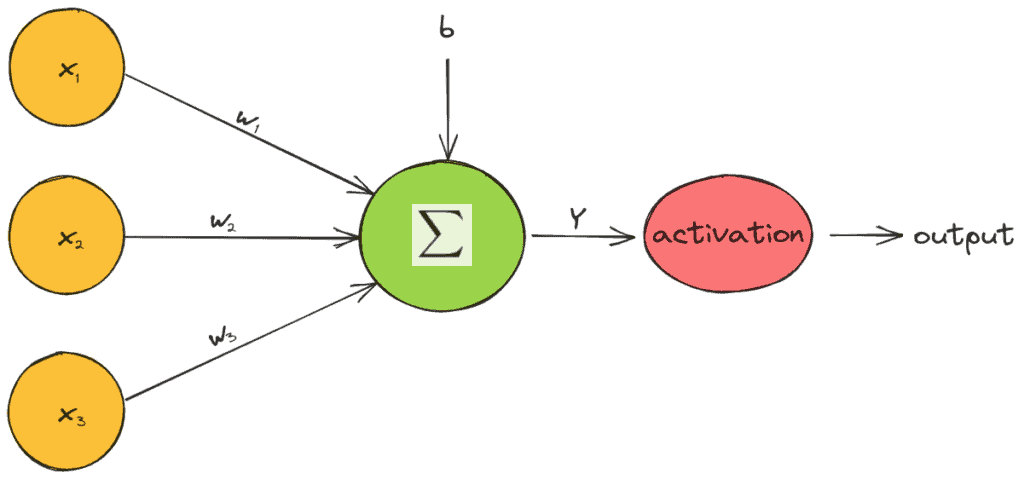
Thus, the activation functions are univariate and non-linear since a network with a linear activation function is equivalent to just a linear regression model. Due to the non-linearity of activation functions, neural networks can capture complex semantic structures and achieve high performance.
The sigmoid activation function (also called logistic function) takes any real value as input and outputs a value in the range . It is calculated as follows:
Here, is the output value of the neuron. Moreover, we can see the plot of the sigmoid function when the input lies in the range
:
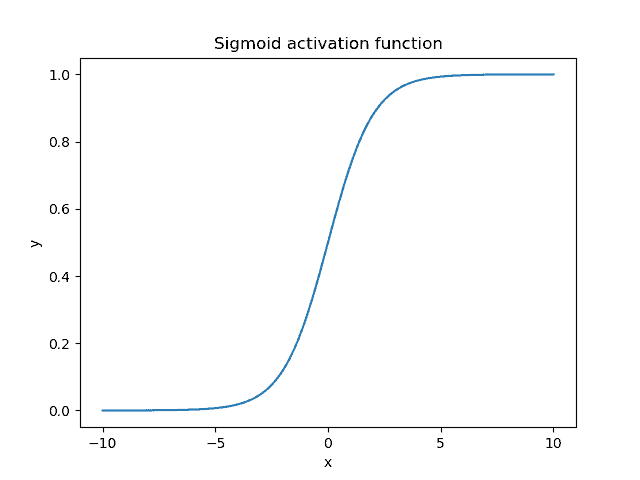
As expected, the sigmoid function is non-linear and bounds the value of a neuron in the small range of . When the output value is close to 1, the neuron is active and enables the flow of information, while a value close to 0 corresponds to an inactive neuron.
Also, an important characteristic of the sigmoid function is that it tends to push the input values to either end of the curve (0 or 1) due to its S-like shape. In the region close to zero, if we slightly change the input value, the respective changes in the output are very large and vice versa. For inputs less than -5, the output of the function is almost zero, while for inputs greater than 5, the output is almost one.
Finally, the output of the sigmoid activation function can be interpreted as a probability since it lies in the range . That’s why it is also used in the output neurons of a prediction task.
Another activation function that is common in deep learning is the tangent hyperbolic function simply referred to as the tanh function. It is calculated as follows:
We observe that the tanh function is a shifted and stretched version of the sigmoid. Below, we can see its plot when the input is in the range :
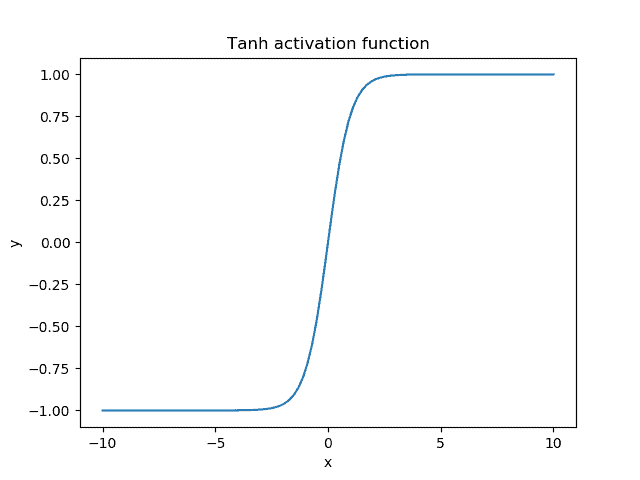
The output range of the tanh function is and presents a similar behavior with the sigmoid function. Thus, the main difference is the fact that the tanh function pushes the input values to 1 and -1 instead of 1 and 0.
Both activation functions have been extensively used in neural networks since they can learn complex structures. Now, let’s compare them, presenting their similarities and differences.
Below, we plot the gradient of the sigmoid (red) and the tanh (blue) activation function:
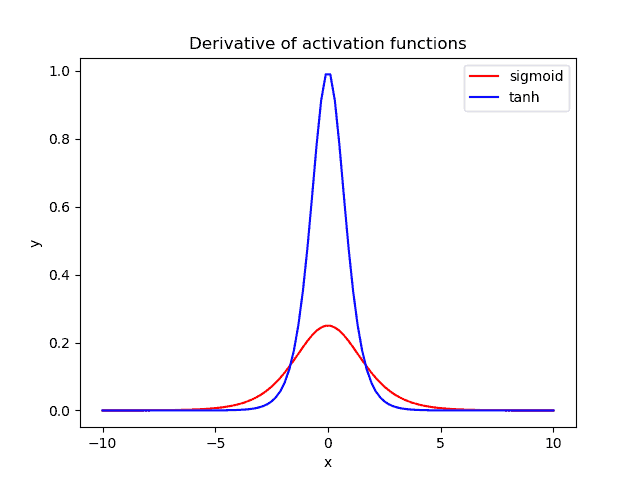
When using these activation functions in a neural network, our data are usually centered around zero. Hence, we should focus on the behavior of each gradient in the region near zero.
Additionally, we observe that the gradient of tanh is four times greater than the gradient of the sigmoid function. This means that using the tanh activation function results in higher gradient values during training and higher updates in the weights of the network. So, if we want strong gradients and big learning steps, we should use the tanh activation function.
Another difference is that the output of tanh is symmetric around zero, leading to faster convergence.
Despite their benefits, both functions present the so-called vanishing gradient problem.
In neural networks, the error is backpropagated through the hidden layers of the network and updates the weights. In case we have a very deep neural network and bounded activation functions like the ones above, the amount of error decreases dramatically after it is backpropagated through each hidden layer. Hence, the error is almost zero at the early layers, and the weights of these layers are not updated properly. Thus, the ReLU activation function can fix the vanishing gradient problem.
Finally, we’ll present an example of applying these activation functions in a simple neuron of two input features and weights
. Therefore, we can see the output value and the gradient when we use the sigmoid (left) and the tanh (right) activation function:
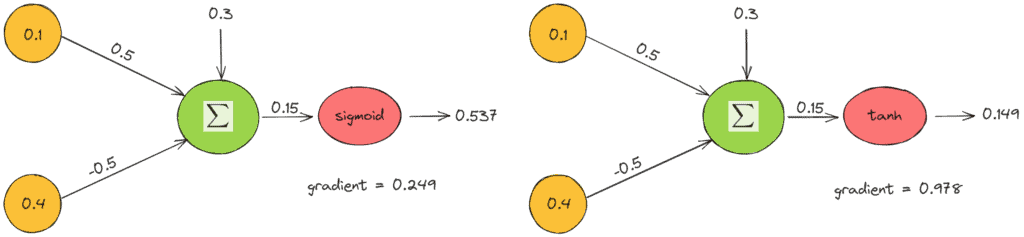
The above example verifies our previous comments. Furthermore, the output value of tanh is closer to zero, and the gradient is four times greater.
Let’s discuss the implementation details of the sigmoid and the tanh activation functions in Python.
We’ll explore three ways to implement the sigmoid activation function in Python.
Our first approach is to use the math module. At the start of the implementation, we define a function for the implementation. Moreover, we add an instruction to implement the sigmoid activation function. Finally, the sigm function returns the value calculated using the sigmoid activation function:
import math
def sigm(x):
s = 1 / (1 + math.exp(-x))
return sAlternatively, we can implement the sigmoid activation function using the numpy library. Let’s take a look at the implementation:
import numpy as np
def sigm(x):
k = np.exp(-x)
s = 1 / (1 + k)
return sFinally, we can use the SciPy library in Python for the implementation. Here, we’re using the expit function from the SciPy library:
from scipy.special import expit
def sigm(x):
s= expit(x)
return sNow, let’s provide some input values:
ip = [-4, -3, -2, 0, 2, 3, 4]
for i in ip:
op = sigm(i)
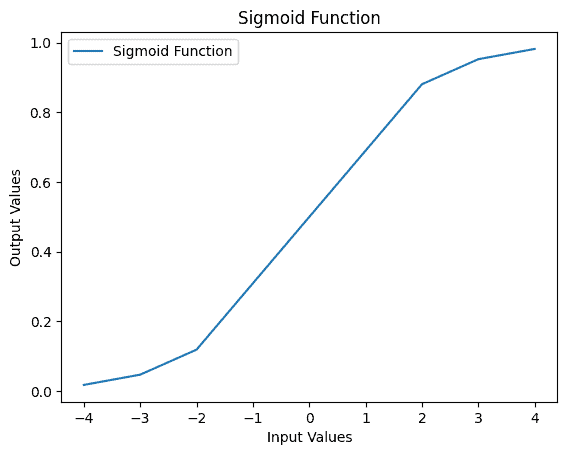
print(f"Input: {i}, Output: {op}")Let’s take a look at the output sigmoid values:
Input: -4, Output: 0.01798620996209156
Input: -3, Output: 0.04742587317756678
Input: -2, Output: 0.11920292202211755
Input: 0, Output: 0.5
Input: 2, Output: 0.8807970779778823
Input: 3, Output: 0.9525741268224334
Input: 4, Output: 0.9820137900379085Finally, we can plot the values using the matplotlib library in Python:
import matplotlib.pyplot as plt
ip = [-4, -3, -2, 0, 2, 3, 4]
op = [sigm(i) for i in ip]
plt.plot(ip, op, label='Sigmoid Function')
plt.xlabel('Input Values')
plt.ylabel('Output Values')
plt.title('Sigmoid Function')
plt.legend()
plt.show()Let’s take a look at the output figure:
Similar to the implementation of the sigmoid activation function, we’ll explore three ways to implement the tanh activation function.
First, we use the math library:
import math
def tanh(x):
t = (math.exp(x) - math.exp(-x)) / (math.exp(x) + math.exp(-x))
return tNext, we utlize the tanh function from the numpy library to calculate the calculate the hyperbolic tangent of an input value:
import numpy as np
def tanh(x):
t = np.tanh(x)
return tAlternatively, we can also use the tanh function from the SciPy library to implement the tanh activation function:
from scipy.special import tanh
def tanh(x):
t = tanh(x)
return tNow, we provide some input values:
ip1 = [-4, -3, -2, 0, 2, 3, 4]
for j in ip1:
op1 = sigm(j)
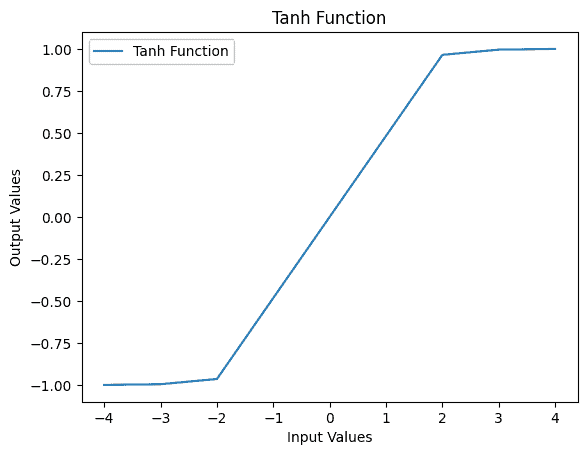
print(f"Input: {j}, Output: {op1}")Let’s take a look at the output values:
Input: -4, Output: -0.9993292997390669
Input: -3, Output: -0.9950547536867306
Input: -2, Output: -0.964027580075817
Input: 0, Output: 0.0
Input: 2, Output: 0.964027580075817
Input: 3, Output: 0.9950547536867306
Input: 4, Output: 0.9993292997390669Furthermore, we utilize the matplotlib library for visualization:
import matplotlib.pyplot as plt
ip1 = [-4, -3, -2, 0, 2, 3, 4]
op1 = [tanh(i) for i in ip1]
plt.plot(ip1, op1, label='Tanh Function')
plt.xlabel('Input Values')
plt.ylabel('Output Values')
plt.title('Tanh Function')
plt.legend()
plt.show()Finally, let’s take a look at the figure that plots all the output values:
In this tutorial, we talked about two activation functions, the tanh and the sigmoid.
We explored the basic idea and compared the two functions with an example. Finally, we provided the implementation details of the tanh and the sigmoid activation functions in Python.