1. Overview
In this tutorial, we’ll discuss an interesting problem in graph theory: vertex coloring. We’ll demonstrate the vertex coloring problem using an example.
Finally, we’ll highlight some solutions and important applications.
2. Introduction
Vertex coloring is a concept in graph theory that refers to assigning colors to the vertices of a graph in such a way that no two adjacent vertices have the same color.
Formally, the vertex coloring of a graph is an assignment of colors. We usually represent the colors by numbers. Additionally, we assign the colors to the vertices such that two adjacent vertices are always filled with different colors.
Furthermore, the minimum number of colors we require to color the vertices of a graph is known as the chromatic number. Generally, this number is always greater than one. However, the chromatic number is equal to one if and only if the graph contains a single vertex.
The concept of vertex coloring is used in many areas of computer science and mathematics. Additionally, we can model complex real-life problems to the vertex coloring problem.
Finding the chromatic number of a graph is difficult and belongs to the NP-complete class. Hence, it’s unlikely that there’s an efficient algorithm to solve it for all graphs. However, for certain special classes of graphs, efficient algorithms exist.
3. Example
Let’s take a graph in order to demonstrate the vertex coloring problem:
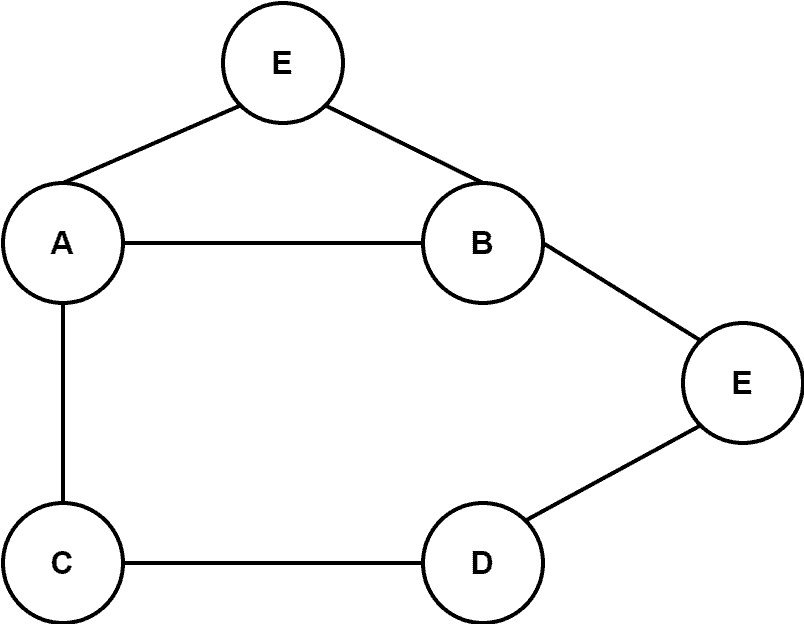
We aim to assign colors to the vertices of the graph in such a way that two adjacent vertices contain different colors:
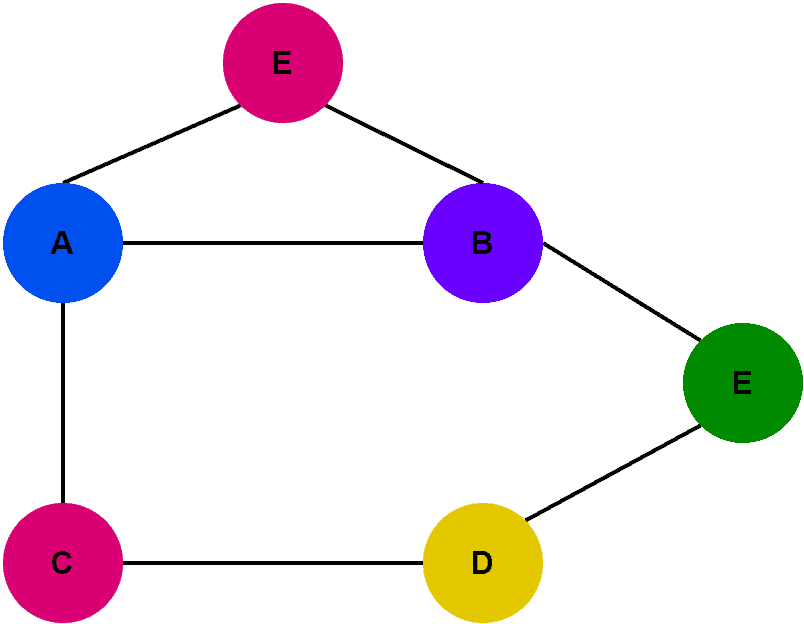
Here, we assign each vertex a color. Additionally, adjacent vertices don’t contain the same color. This’s a solution to the vertex coloring problem. However, we’ve used five different colors. Now let’s try to reduce the number of colors used here:
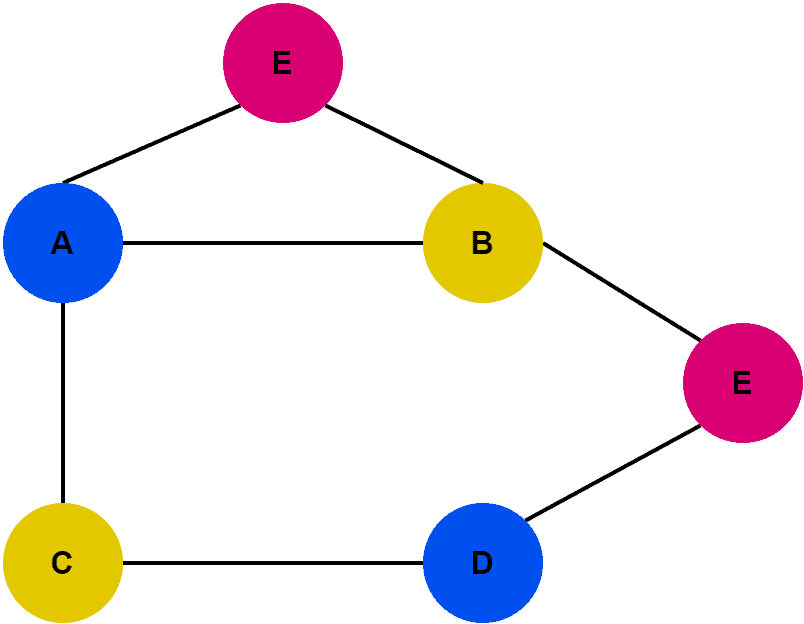
Here, we successfully reduced the number of colors from 5 to 3. We can’t reduce it further as we need a minimum of 3 colors to color all the vertices of . Hence, the chromatic number of graph
is 3.
4. Solutions
Let’s discuss some approaches to solving the vertex coloring problem.
The most basic but not so-efficient approach is brute force search. A brute force search algorithm involves trying all possible colorings of the graph and selecting the one with the minimum number of colors. While this algorithm is guaranteed to find an optimal solution, it’s computationally expensive. Additionally, this approach is only feasible for small graphs.
The second approach is local search. Local search algorithms iteratively improve an existing solution by making small local changes. In the case of the vertex coloring problem, a local search algorithm might swap the colors of two vertices that are adjacent. Additionally, it may try to recolor a single vertex. Local search algorithms can be efficient and effective, especially when combined with other techniques.
We can also formulate the vertex coloring problem as an integer linear program. This approach can find exact solutions to the problem. However, it can be computationally expensive for large graphs.
Finally, we can use greedy methods to solve the vertex coloring problem. These algorithms are simple and efficient. However, they don’t always produce an optimal solution.
5. Applications
Vertex coloring is an important problem in graph theory. Additionally, it has many applications in computer science, operations research, and other fields. Some of the most common applications of the vertex coloring problem include scheduling, routing, register allocation, and wireless frequency assignment.
In the scheduling problem, we must assign resources to the available tasks and avoid conflicts. To solve this problem, we can represent each task as a vertex and each resource as a color in a graph. Furthermore, we can determine the chromatic number from this graph. Hence, the chromatic number represents the minimum number of resources needed to complete all tasks without conflicts.
Let’s talk about the network routing problem. In routing, data packets must be routed through a network of nodes without conflicts. Furthermore, we can use vertex coloring to model this problem, with each node representing a vertex and each path representing a color in the graph. Additionally, the chromatic number denotes the least possible number of paths required to route all packets without conflicts.
In compilers, variables in a program must be assigned to registers in a computer’s processor. We can utilize vertex coloring and chromatic number concepts in order to provide the least possible number of registers needed to execute the program.
Finally, in wireless network communication, the vertex coloring problem can be used for the frequency assignment of wireless channels for devices to avoid interference.
6. Conclusion
In this tutorial, we discussed the vertex coloring problem. We presented some solutions along with an example demonstrating how to solve the vertex coloring problem.
Finally, we highlighted some important applications.