Introduction to Greedy Algorithms with Java

1. Introduction

In this tutorial, we’re going to introduce greedy algorithms in the Java ecosystem.

2. Greedy Problem

When facing a mathematical problem, there may be several ways to design a solution. We can implement an iterative solution, or some advanced techniques, such as divide and conquer principle (e.g. Quicksort algorithm) or approach with dynamic programming (e.g. Knapsack problem) and many more.

Most of the time, we’re searching for an optimal solution, but sadly, we don’t always get such an outcome. However, there are cases where even a suboptimal result is valuable. With the help of some specific strategies, or heuristics, we might earn ourselves such a precious reward.

In this context, given a divisible problem, a strategy that at each stage of the process takes the locally optimal choice or “greedy choice” is called a greedy algorithm.

We stated that we should address a “divisible” problem: A situation that can be described as a set of subproblems with, almost, the same characteristics. As a consequence, most of the time, a greedy algorithm will be implemented as a recursive algorithm.

A greedy algorithm can be a way to lead us to a reasonable solution in spite of a harsh environment; lack of computational resources, execution-time constraint, API limitations, or any other kind of restrictions.

2.1. Scenario

In this short tutorial, we’re going to implement a greedy strategy to extract data from a social network using its API.

Let’s say we’d like to reach more users on the “little-blue-bird” social. The best way to achieve our goal is to post original content or re-tweet something that will arouse some interest to a broad audience.

How do we find such an audience? Well, we must find an account with many followers and tweet some content for them.

2.2. Classic vs. Greedy

We take into account the following situation: Our account has four followers, each of which has, as depicted in the image below, respectively 2, 2, 1 and 3 followers, and so on:

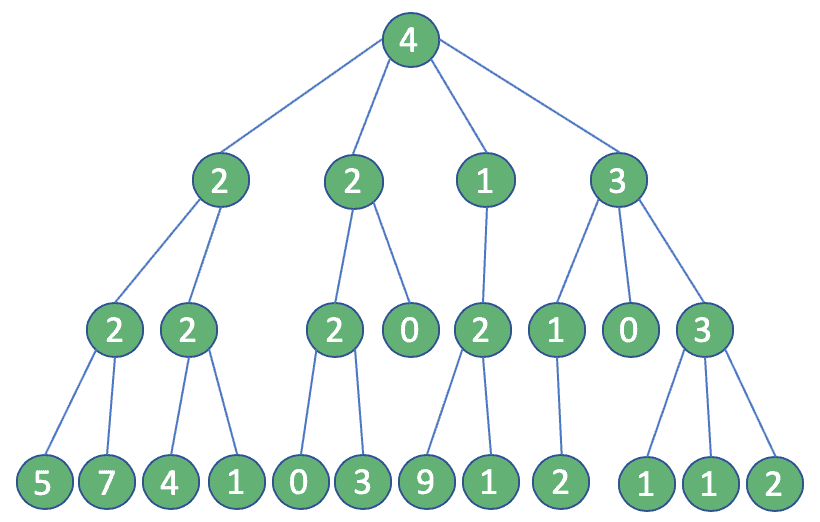
With this purpose in our minds, we’ll take the one with more followers among the followers of our account. Then we’ll repeat the process two more times until we reach the 3rd degree of connection (four steps in total).

In this way, we define a path made of users, leading us to the vastest followers-base from our account. If we can address some content to them, they’ll surely reach our page.

We can start with a “traditional” approach. At every single step, we’ll perform a query to get the followers of an account. As a result of our selection process, the number of accounts will increase every step.

Surprisingly, in total, we would end up performing 25 queries:

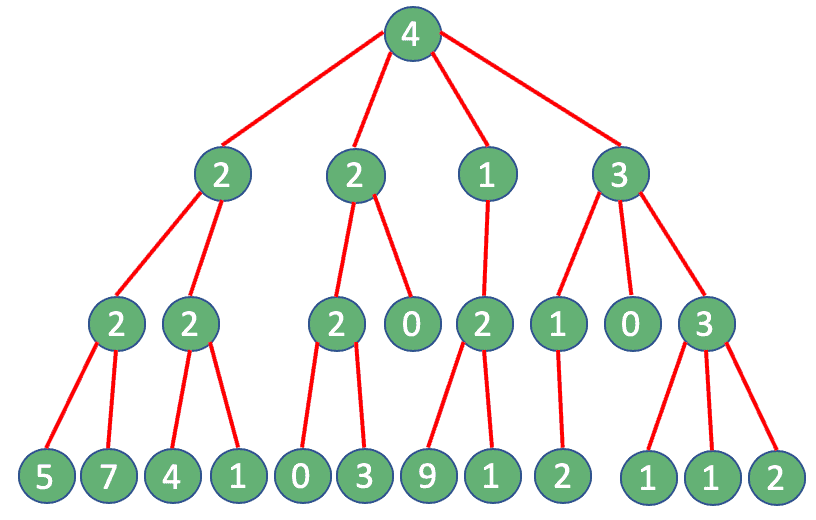
Here a problem arises: For example, Twitter API limits this type of query to 15 every 15 minutes. If we try to perform more calls than allowed, we’ll get a “Rate limit exceeded code – 88“, or “Returned in API v1.1 when a request cannot be served due to the application’s rate limit having been exhausted for the resource“. How can we overcome such a limit?

Well, the answer is right in front of us: A greedy algorithm. If we use this approach, at each step, we can assume that the user with the most followers is the only one to consider: In the end, we need only four queries. Quite an improvement!

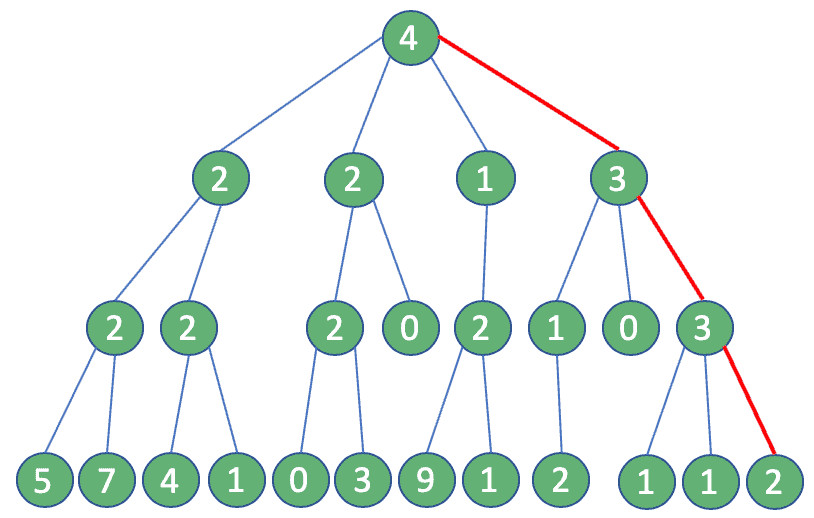
The outcome of those two approaches will be different. In the first case, we get 16, the optimal solution, while in the latter, the maximum number of reachable followers is merely 12.

Will this difference be so valuable? We’ll decide later.

3. Implementation

To implement the above logic, we initialize a small Java program, where we’ll mimic the Twitter API. We’ll also make use of the Lombok library.

Now, let’s define our component SocialConnector in which we’ll implement our logic. Note that we’re going to put a counter to simulate calls restrictions, but we’ll lower it to four:

public class SocialConnector {
    private boolean isCounterEnabled = true;
    private int counter = 4;
    @Getter @Setter
    List users;

    public SocialConnector() {
        users = new ArrayList<>();
    }

    public boolean switchCounter() {
        this.isCounterEnabled = !this.isCounterEnabled;
        return this.isCounterEnabled;
    }
}

Then we’re going to add a method to retrieve the followers’ list of a specific account:

public List getFollowers(String account) {
    if (counter < 0) {
        throw new IllegalStateException ("API limit reached");
    } else {
        if (this.isCounterEnabled) {
            counter--;
        }
        for (SocialUser user : users) {
            if (user.getUsername().equals(account)) {
                return user.getFollowers();
            }
        }
     }
     return new ArrayList<>();
}

To support our process, we need some classes to model our user entity:

public class SocialUser {
    @Getter
    private String username;
    @Getter
    private List<SocialUser> followers;

    @Override
    public boolean equals(Object obj) {
        return ((SocialUser) obj).getUsername().equals(username);
    }

    public SocialUser(String username) {
        this.username = username;
        this.followers = new ArrayList<>();
    }

    public SocialUser(String username, List<SocialUser> followers) {
        this.username = username;
        this.followers = followers;
    }

    public void addFollowers(List<SocialUser> followers) {
        this.followers.addAll(followers);
    }
}

3.1. Greedy Algorithm

Finally, it’s time to implement our greedy strategy, so let’s add a new component – GreedyAlgorithm – in which we’ll perform the recursion:

public class GreedyAlgorithm {
    int currentLevel = 0;
    final int maxLevel = 3;
    SocialConnector sc;
    public GreedyAlgorithm(SocialConnector sc) {
        this.sc = sc;
    }
}

Then we need to insert a method findMostFollowersPath in which we’ll find the user with most followers, count them, and then proceed to the next step:

public long findMostFollowersPath(String account) {
    long max = 0;
    SocialUser toFollow = null;

    List followers = sc.getFollowers(account);
    for (SocialUser el : followers) {
        long followersCount = el.getFollowersCount();
        if (followersCount > max) {
            toFollow = el;
            max = followersCount;
        }
    }
    if (currentLevel < maxLevel - 1) {
        currentLevel++;
        max += findMostFollowersPath(toFollow.getUsername());
    } 
    return max;
}

Remember: Here is where we perform a greedy choice. As such, every time we call this method, we’ll choose one and only one element from the list and move on: We won’t ever go back on our decisions!

Perfect! We are ready to go, and we can test our application. Before that, we need to remember to populate our tiny network and finally, execute the following unit test:

public void greedyAlgorithmTest() {
    GreedyAlgorithm ga = new GreedyAlgorithm(prepareNetwork());
    assertEquals(ga.findMostFollowersPath("root"), 5);
}

3.2. Non-Greedy Algorithm

Let’s create a non-greedy method, merely to check with our eyes what happens. So, we need to start with building a NonGreedyAlgorithm class:

public class NonGreedyAlgorithm {
    int currentLevel = 0;
    final int maxLevel = 3; 
    SocialConnector tc;

    public NonGreedyAlgorithm(SocialConnector tc, int level) {
        this.tc = tc;
        this.currentLevel = level;
    }
}

Let’s create an equivalent method to retrieve followers:

public long findMostFollowersPath(String account) {		
    List<SocialUser> followers = tc.getFollowers(account);
    long total = currentLevel > 0 ? followers.size() : 0;

    if (currentLevel < maxLevel ) {
        currentLevel++;
        long[] count = new long[followers.size()];
        int i = 0;
        for (SocialUser el : followers) {
            NonGreedyAlgorithm sub = new NonGreedyAlgorithm(tc, currentLevel);
            count[i] = sub.findMostFollowersPath(el.getUsername());
            i++;
        }

        long max = 0;
        for (; i > 0; i--) {
            if (count[i-1] > max) {
                max = count[i-1];
            }
        }		
        return total + max;
     }	
     return total;
}

As our class is ready, we can prepare some unit tests: One to verify the call limit exceeds and another one to check the value returned with a non-greedy strategy:

public void nongreedyAlgorithmTest() {
    NonGreedyAlgorithm nga = new NonGreedyAlgorithm(prepareNetwork(), 0);
    Assertions.assertThrows(IllegalStateException.class, () -> {
        nga.findMostFollowersPath("root");
    });
}

public void nongreedyAlgorithmUnboundedTest() {
    SocialConnector sc = prepareNetwork();
    sc.switchCounter();
    NonGreedyAlgorithm nga = new NonGreedyAlgorithm(sc, 0);
    assertEquals(nga.findMostFollowersPath("root"), 6);
}

4. Results

It’s time to review our work!

First, we tried out our greedy strategy, checking its effectiveness. Then we verified the situation with an exhaustive search, with and without the API limit.

Our quick greedy procedure, which makes locally optimal choices each time, returns a numeric value. On the other hand, we don’t get anything from the non-greedy algorithm, due to an environment restriction.

Comparing the two methods’ output, we can understand how our greedy strategy saved us, even if the retrieved value that is not optimal. We can call it a local optimum.

5. Conclusion

In mutable and fast-changing contexts like social media, problems that require finding an optimal solution can become a dreadful chimera: Hard to reach and, at the same time, unrealistic.

Overcoming limitations and optimizing API calls is quite a theme, but, as we’ve discussed, greedy strategies are effective. Choosing this kind of approach saves us much pain, returning valuable results in exchange.

Keep in mind that not every situation is suitable: We need to evaluate our circumstances every time.