What Are Planar Graphs? | Baeldung on Computer Science

1. Introduction

In this tutorial, we’ll talk about planar graphs and present some of their fundamental properties.

2. Planar Graphs

A planar graph $\boldsymbol{G = (V, E)}$ is the one we can draw on the plane so that its edges don’t cross (except at nodes). A graph drawn in that way is also also known as a planar embedding or a plane graph.

So, there’s a difference between planar and plane graphs. A plane graph has no edge crossings, but a planar graph may be drawn without them. For example:

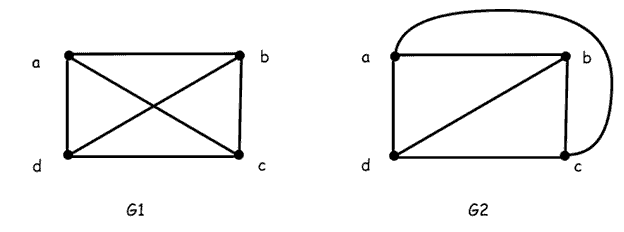
$G_1$ is a planar but not a plane graph, whereas $G_2$ is a plane graph. $G_1$ is planar because it is isomorphic to $G_2$ .

2.1. Isomorphism

Formally, a planar graph is isomorphic to a plane graph.

$G_1(V_1, E_1)$ and $G_2(V_2, E_2)$ are isomorphic graphs if there’s a 1-1 mapping $F: V_1 \rightarrow V_2$ of their vertices, and the following holds:

$\forall (u, v) \in V_1, (u, v) \in E1 \iff (F(u), F(v)) \in E_2$

For example:

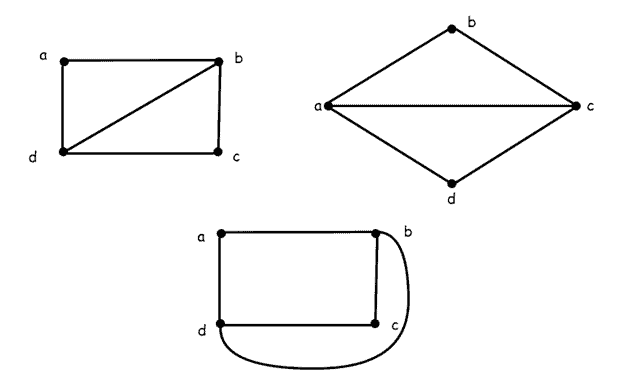
All three graphs are isomorphic to one another. The top left and the bottom graphs have the identity isomorphism ( $F(u)=u$ ), whereas the isomorphism of the top right graph is $F(a)=d, F(c)=b, F(d)=c, F(b)=a$ .

3. Properties of Planar Graphs

Let’s check out some properties of planar graphs.

3.1. Faces

A graph defines connected regions on a plane we call faces, each of which is bordered by graph edges:

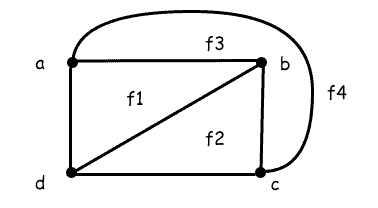
Any face’s boundary contains the vertices and edges of the graph $G$ that separate it from other regions.

One unbounded region, known as the exterior region, exists in every plane graph.

The number of edges constituting the boundary of a face $f$ is its degree. In other terms, the length of the face’s boundary determines its degree.

For instance, the faces $f_1$ , $f_2$ , and $f_3$ of $G$ in the above image have the degree of $d(f_1)=d(f_2)=d(f_3)=3$ .

3.2. Chromatic Number

As we recall from graph theory, the chromatic number of a graph is the least amount of colors necessary to color the vertices of a graph G such that no two adjacent nodes have the same color. Any planar graph’s chromatic number is always less than or equal to 4.

As a result, any planar graph always requires a maximum of four colors to color its vertices. For instance:

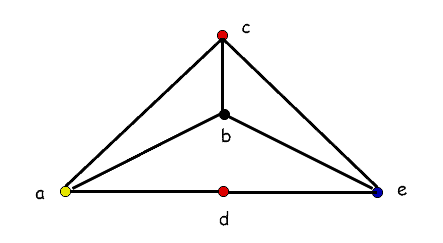
This planar graph’s chromatic number is 4.

3.3. Proving a Graph Is (Not) Planar

There are several properties of planar graphs we can use in proofs:

If a connected planar graph $G$ has $e$ edges and $r$ regions or faces then $r\leq \frac{2}{3} e$
If a connected planar graph $G$ has $e$ edges, $v$ vertices, and $r$ regions, then $v - e + r = 2$
If a connected planar graph $G$ has $e$ edges and $v$ vertices, then $3v -e \geq 6$
A complete graph $K_n$ is a planar iff $n < 5$
A complete bipartite graph $K_{m,n}$ is planar iff $m<3$ or $n \geq 3$
If and only if a subgraph of graph $G$ is homomorphic to $K_5$ or $K_{3, 3}$ , then $G$ is considered to be non-planar

A graph homomorphism is a mapping between two graphs that considers their structural differences. More precisely, a graph $G=(V, E)$ is homomorphic to $G'=(V', E')$ if there’s a mapping $f: V \rightarrow V'$ such that $(x, y) \in E \implies (f(x, f(y)) \in E'$ . It maps vertices adjacent in $G$ to vertices adjacent in $G'$ .

The first three state the necessary conditions for planarity. For example, if we have a connected graph such that $3v - e < 6$ , we know it isn’t planar. However, necessary conditions aren’t sufficient, which means that some non-planar graphs can satisfy them. Therefore, we can use those properties to prove that a graph isn’t planar, not that it is.

The last property allows us to prove if a graph is planar. If we can’t find $\boldsymbol{K_5}$ or $\boldsymbol{K_{3,3}}$ in our graph, then we can be sure it’s planar.

3.4. Non-Planar Graphs

Non-planar graphs can’t be drawn in a plane without crossing edges.

Two well-known types of non-planar graphs are $K_5$ , a complete graph with 5 vertices, and $K_{3, 3}$ , a complete bipartite graph with 3 vertices in each bipartition:

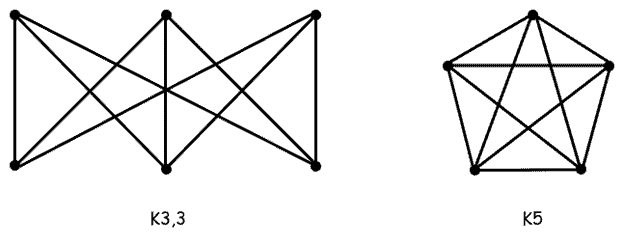
The importance of these two graphs lies in the fact that any non-planar graph contains them as subgraphs.

4. Conclusion

In this article, we discussed planar graphs, one of the most widely used graph theory concepts.

A planar graph is a graph that can be drawn on a plane such that its edges intersect only at their end nodes. A plane graph is a graph whose edges don’t intersect. So, we call a graph planar if we can draw it as a plane graph.

To prove that a graph is planar, we need to show that it doesn’t contain the complete graph $\boldsymbol{K_5}$ or the complete bipartite graph $\boldsymbol{K_{3,3}}$ .

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex