1. Introduction
In this tutorial, we’ll explain the Tabu Search algorithm.
2. Tabu Search and Optimization
Optimization methods are generally divided into exact and approximative. Metaheuristics constitute a popular subcategory of the latter. Genetic algorithms, Ant Colony Optimization, PSO, and Simulated Annealing, are notable examples of metaheuristics.
Tabu Search is a local-search metaheuristic we use for combinatorial optimization problems.
2.1. Local Search
Local-search methods start with a potential solution and examine its neighborhood to locate a better neighbor. Afterward, they do the same with the neighbor. This goes on iteratively until we find the optimum or break the stopping conditions pre-defined by users.
Local search has two limitations:
- It can frequently become trapped at local optima or stuck at plateaus (parts of the search space that have the same value as the objective function)
- It can keep revisiting the same solution or set of solutions (this we call the cycling problem)
We see that both problems can occur even in one-dimensional search spaces:
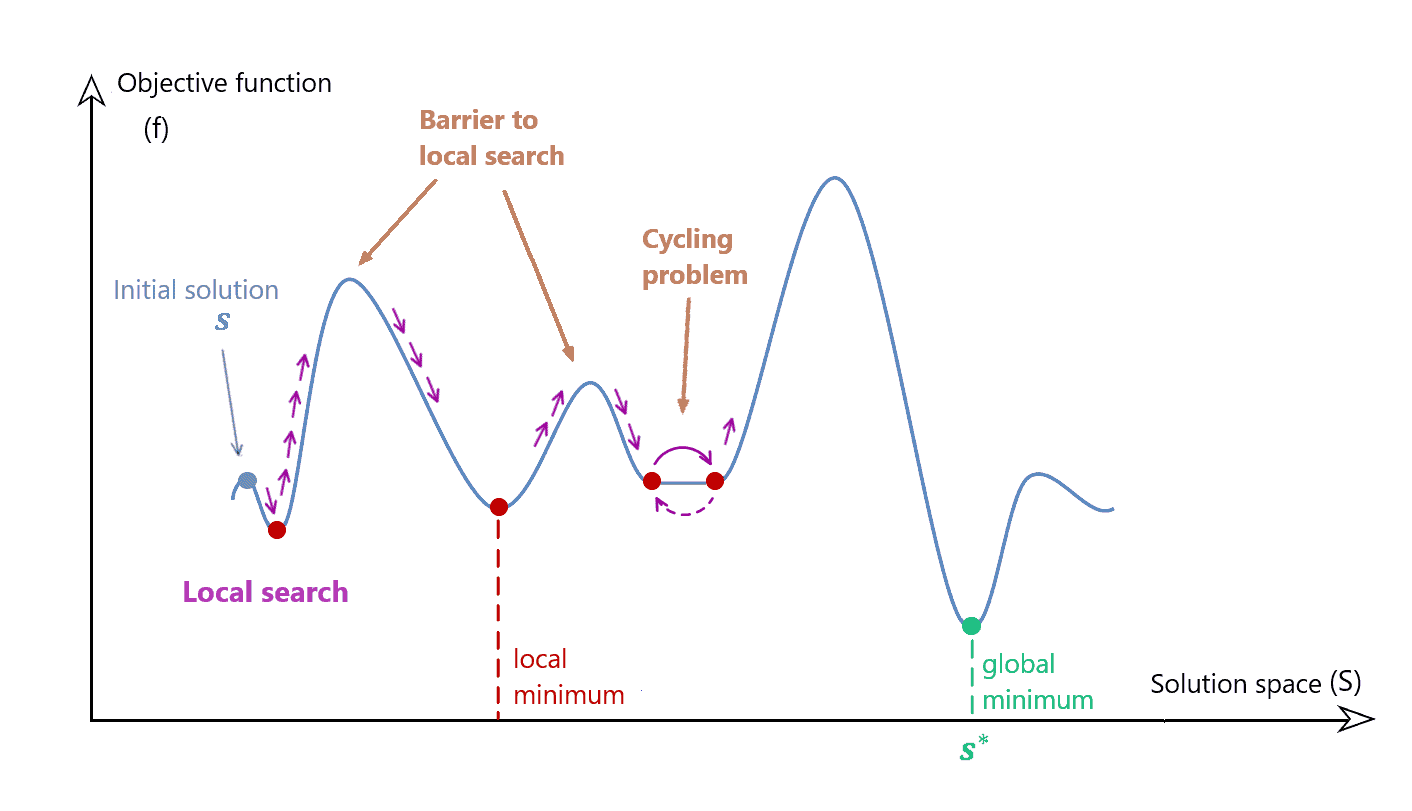
This is where TS plays a key role. It was specifically designed to avoid these problems.
3. Ingredients of Tabu Search
In each iteration, Tabu Search evaluates a sample of neighbors of the current solution. Then, it retains the best among them even if it’s worse than the current solution or the best solution found before that iteration. This allows the algorithm to escape from local optima.
However, the distinctive feature of TS is that it avoids tabu solutions.
3.1. Tabu
In each iteration, TS checks and possibly updates the tabu list which contains the forbidden solutions. Usually, those are the recently visited solutions. By forbidding them, we encourage Tabu Search to explore different regions of the search space. If a solution has been in the tabu list for more than iterations, we remove it from there. The value of
is pre-defined by the user.
However, the tabu list can contain tabu rules. They describe the solutions that should be avoided. For example, they can be problem-specific constraints or hypotheses defined by the user. Also, they can define the expiration time of a solution’ tabu state or the length of the tabu list. So, a tabu solution isn’t necessarily visited. It can get its tabu status by falling under the scope of a tabu rule.
To maintain the tabu list, we need to supply TS with the definition of a neighborhood and the aspiration criteria.
3.2. Neighborhood
The neighborhood of a solution
in the
th iteration is the set of the solutions adjacent to
in the search space
in that iteration
.
For example, we may define as the set of all the solutions whose distance to
is at most
. If the threshold distance
isn’t the same for every
, we have an adaptive neighborhood. However,
can be a constant with respect to
.
3.3. Aspiration Criteria
The aspiration criteria are the rules by which we can strip a solution of its tabu status in the
th iteration. For example,
can redeem the solution whose objective-function value is better than that of any other solution in the current iteration. If the criteria at the iteration
allow
, we’ll say that
, and vice versa.
So, TS will move to a solution in two cases: if it isn’t in the tabu list and if the aspiration criteria allow it regardless of its membership in the tabu list.
4. Pseudocode
Let denote the objective function to optimize and
the maximum number of iterations. The following pseudocode presents Tabu Search:
Overall, the settings of the algorithm’s parameters determine whether to prioritize intensification or diversification through the search process at a given time. In order to solve combinatorial optimization issues, metaheuristics must find a compromise between these two factors.
5. Conclusion
In this tutorial, we introduced Tabu Search, a local-search metaheuristic. It differs from other metaheuristics by directing the search using its search history.
