Graphs in Java

1. Overview

In this tutorial, we’ll look at the basic concepts of a graph as a data structure.

We’ll also explore its implementation in Java along with various operations possible on a graph. We will also discuss the Java libraries offering graph implementations.

2. Graph Data Structure

A graph is a data structure for storing connected data such as a network of people on a social media platform.

A graph consists of vertices and edges. A vertex represents the entity (e.g., people) and an edge represents the relationship between entities (e.g., a person’s friendships).

Let’s define a simple Graph to understand this better:

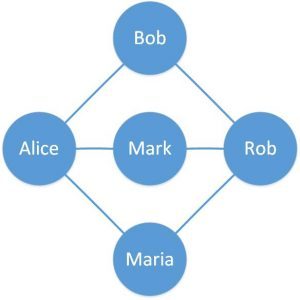
Here we’ve defined a simple graph with five vertices and six edges. The circles are vertices representing people and the lines connecting two vertices are edges representing friends on an online portal.

There are a few variations of this simple graph depending on the properties of the edges. Let’s briefly go through them in the next sections.

However, we’ll only focus on the simple graph presented here for the Java examples in this tutorial.

2.1. Directed Graph

The graph we’ve defined so far has edges without any direction. If these edges feature a direction in them, the resulting graph is known as a directed graph.

An example of this can be representing who sent the friend request in a friendship on the online portal:

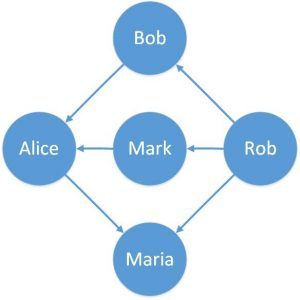
Here we can see that the edges have a fixed direction. The edges can be bidirectional as well.

2.2. Weighted Graph

Again, our simple graph has edges that are unbiased or unweighted.

If instead these edges carry relative weight, this graph is known as a weighted graph.

An example of a practical application of this can be representing how relatively old a friendship is on the online portal:

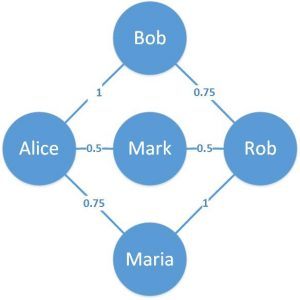
Here we can see that the edges have weights associated with them. This provides a relative meaning to these edges.

3. Graph Representations

A graph can be represented in different forms such as adjacency matrix and adjacency list. Each one has their pros and cons in a different setup.

We’ll introduce these graph representations in this section.

3.1. Adjacency Matrix

An adjacency matrix is a square matrix with dimensions equivalent to the number of vertices in the graph.

The elements of the matrix typically have values 0 or 1. A value of 1 indicates adjacency between the vertices in the row and column and a value of 0 otherwise.

Let’s see what the adjacency matrix looks like for our simple graph from the previous section:

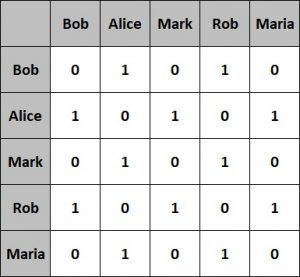
This representation is fairly easier to implement and efficient to query as well. However, it’s less efficient with respect to space occupied.

3.2. Adjacency List

An adjacency list is nothing but an array of lists. The size of the array is equivalent to the number of vertices in the graph.

The list at a specific index of the array represents the adjacent vertices of the vertex represented by that array index.

Let’s see what the adjacency list looks like for our simple graph from the previous section:

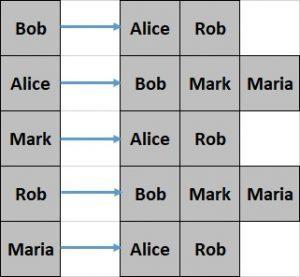
This representation is comparatively difficult to create and less efficient to query. However, it offers better space efficiency.

We’ll use the adjacency list to represent the graph in this tutorial.

4. Graphs in Java

Java doesn’t have a default implementation of the graph data structure.

However, we can implement the graph using Java Collections.

Let’s begin by defining a vertex:

class Vertex {
    String label;
    Vertex(String label) {
        this.label = label;
    }

    // equals and hashCode
}

The above definition of vertex just features a label, but this can represent any possible entity such as Person or City.

Also, note that we have to override the equals() and hashCode() methods as these are necessary to work with Java Collections.

As we discussed earlier, a graph is nothing but a collection of vertices and edges that can be represented as either an adjacency matrix or an adjacency list.

Let’s see how we can define this using an adjacency list here:

class Graph {
    private Map<Vertex, List<Vertex>> adjVertices;
    
    // standard constructor, getters, setters
}

As we can see, the class Graph is using Map from Java Collections to define the adjacency list.

There are several operations possible on a graph data structure, such as creating, updating or searching through the graph.

We’ll go through some of the more common operations and see how we can implement them in Java.

5. Graph Mutation Operations

To start with, we’ll define some methods to mutate the graph data structure.

Let’s define methods to add and remove vertices:

void addVertex(String label) {
    adjVertices.putIfAbsent(new Vertex(label), new ArrayList<>());
}

void removeVertex(String label) {
    Vertex v = new Vertex(label);
    adjVertices.values().stream().forEach(e -> e.remove(v));
    adjVertices.remove(new Vertex(label));
}

These methods simply add and remove elements from the vertices Set.

Now let’s also define a method to add an edge:

void addEdge(String label1, String label2) {
    Vertex v1 = new Vertex(label1);
    Vertex v2 = new Vertex(label2);
    adjVertices.get(v1).add(v2);
    adjVertices.get(v2).add(v1);
}

This method creates a new Edge and updates the adjacent vertices Map.

In a similar way, we’ll define the removeEdge() method:

void removeEdge(String label1, String label2) {
    Vertex v1 = new Vertex(label1);
    Vertex v2 = new Vertex(label2);
    List<Vertex> eV1 = adjVertices.get(v1);
    List<Vertex> eV2 = adjVertices.get(v2);
    if (eV1 != null)
        eV1.remove(v2);
    if (eV2 != null)
        eV2.remove(v1);
}

Next, let’s see how we can create the simple graph we drew earlier using the methods we’ve defined so far:

Graph createGraph() {
    Graph graph = new Graph();
    graph.addVertex("Bob");
    graph.addVertex("Alice");
    graph.addVertex("Mark");
    graph.addVertex("Rob");
    graph.addVertex("Maria");
    graph.addEdge("Bob", "Alice");
    graph.addEdge("Bob", "Rob");
    graph.addEdge("Alice", "Mark");
    graph.addEdge("Rob", "Mark");
    graph.addEdge("Alice", "Maria");
    graph.addEdge("Rob", "Maria");
    return graph;
}

Finally, we’ll define a method to get the adjacent vertices of a particular vertex:

List<Vertex> getAdjVertices(String label) {
    return adjVertices.get(new Vertex(label));
}

6. Traversing a Graph

Now that we have the graph data structure and functions to create and update it defined, we can define some additional functions for traversing the graph.

We need to traverse a graph to perform any meaningful action, such as search within the graph.

There are two possible ways to traverse a graph: depth-first traversal and breadth-first traversal.

6.1. Depth-First Traversal

A depth-first traversal starts at an arbitrary root vertex and explores vertices as deep as possible along each branch before exploring vertices at the same level.

Let’s define a method to perform the depth-first traversal:

Set<String> depthFirstTraversal(Graph graph, String root) {
    Set<String> visited = new LinkedHashSet<String>();
    Stack<String> stack = new Stack<String>();
    stack.push(root);
    while (!stack.isEmpty()) {
        String vertex = stack.pop();
        if (!visited.contains(vertex)) {
            visited.add(vertex);
            for (Vertex v : graph.getAdjVertices(vertex)) {              
                stack.push(v.label);
            }
        }
    }
    return visited;
}

Here, we’re using a Stack to store the vertices that need to be traversed.

Let’s run this on the graph we created in the previous subsection:

assertEquals("[Bob, Rob, Maria, Alice, Mark]", depthFirstTraversal(graph, "Bob").toString());

Please note that we’re using vertex “Bob” as our root for traversal here, but this can be any other vertex.

6.2. Breadth-First Traversal

Comparatively, a breadth-first traversal starts at an arbitrary root vertex and explores all neighboring vertices at the same level before going deeper in the graph.

Now let’s define a method to perform the breadth-first traversal:

Set<String> breadthFirstTraversal(Graph graph, String root) {
    Set<String> visited = new LinkedHashSet<String>();
    Queue<String> queue = new LinkedList<String>();
    queue.add(root);
    visited.add(root);
    while (!queue.isEmpty()) {
        String vertex = queue.poll();
        for (Vertex v : graph.getAdjVertices(vertex)) {
            if (!visited.contains(v.label)) {
                visited.add(v.label);
                queue.add(v.label);
            }
        }
    }
    return visited;
}

Note that a breadth-first traversal makes use of Queue to store the vertices that need to be traversed.

Let’s again run this traversal on the same graph:

assertEquals(
  "[Bob, Alice, Rob, Mark, Maria]", breadthFirstTraversal(graph, "Bob").toString());

Again, the root vertex, which is “Bob” here, can just as well be any other vertex.

7. Java Libraries for Graphs

It’s not necessary to always implement the graph from scratch in Java. There are several open source and mature libraries available that offer graph implementations.

In the next few subsections, we’ll go through some of these libraries.

7.1. JGraphT

JGraphT is one of the most popular libraries in Java for the graph data structure. It allows the creation of a simple graph, directed graph and weighted graph, among others.

Additionally, it offers many possible algorithms on the graph data structure. One of our previous tutorials covers JGraphT in much more detail.

7.2. Google Guava

Google Guava is a set of Java libraries that offer a range of functions including graph data structure and its algorithms.

It supports creating simple Graph, ValueGraph and Network. These can be defined as Mutable or Immutable.

7.3. Apache Commons

Apache Commons is an Apache project that offers reusable Java components. This includes Commons Graph that offers a toolkit to create and manage graph data structure. This also provides common graph algorithms to operate on the data structure.

7.4. Sourceforge JUNG

Java Universal Network/Graph (JUNG) is a Java framework that provides extensible language for modeling, analysis and visualization of any data that can be represented as a graph.

JUNG supports many algorithms that include routines such as clustering, decomposition and optimization.

These libraries provide a number of implementations based on the graph data structure. There are also more powerful frameworks based on graphs, such as Apache Giraph, currently used at Facebook to analyze the graphs formed by their users, and Apache TinkerPop, commonly used on top of graph databases.

8. Conclusion

In this article, we discussed the graph as a data structure along with its representations. We defined a very simple graph in Java using Java Collections and also defined common traversals for the graph.

We also talked briefly about various libraries available in Java outside the Java platform that provide graph implementations.

As always, the code for the examples is available over on GitHub.