What Is the Difference Between a Directed and an Undirected Graph

1. Overview

In this tutorial, we’ll study the differences between directed and undirected graphs. We’ll also learn what are the cases in which we should prefer using one over the other.

At first, we’ll discuss the relationship between graphs and network theory, on one hand, and graphs and information theory, on the other. In doing so, we’ll learn a definition of entropy for graphs that allows us to compare directed with undirected graphs.

2. Graphs, Edges, and Relationships

2.1. Graphs or Networks?

Programmers talk frequently about networks, but they get often confused when the discussion shifts to graphs. Graphs, in common sense, are the figurative representations of functions.

Let’s imagine we have a network comprised of a set of nodes linked, or not linked, by a given relationship $R$ :

Internet or LANs can be modeled as networks, where each element is a computer and each link is a connection. This network can be considered as a system whose elements interact with one another, and give rise to a behavior that is emergent and often not reducible to the aggregate behavior of its components.

Networks of interrelated elements can be found in nature, in social systems, and in informatics, and are the subject of study of a discipline called network theory.

In graph theory, the mathematical counterpart of network theory, a network is called a graph, its nodes are called vertices, and the set of links are called edges. For the rest of this article, we’ll be using the terminology of graph theory, but keep in mind that this corresponds perfectly to the one associated with network theory:

2.2. Graphs in Information Theory

Graphs are important data structures in computer science because they allow us to work not only with the values of objects but also with the relationships existing between them. Some typical applications of graphs in computer science involve knowledge representation, symbolic reasoning, multi-agent simulations, and modeling of dynamical systems.

Graphs are also important because they are well studied under an information-theoretic perspective. For this article, since we’re discussing the difference between directed and undirected graphs, we’re interested in the measurement of one important characteristic of graphs: their entropy.

As we’ll see, we can’t treat directed and undirected graphs as if they were equal, without paying a price in terms of entropy.

2.3. Graphs and Entropy

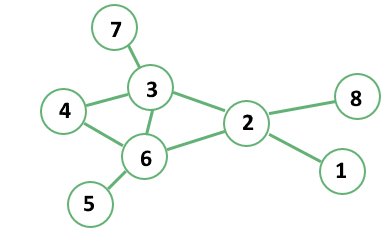
One common definition of entropy in a graph involves the so-called adjacency matrix. The adjacency matrix $M$ of a graph is a matrix where all row and columns represent the set of vertices belonging to that graph.

In the adjacency matrix, all rows indicate a tail or a start of a potential edge, while the columns indicate the head or target of that edge:

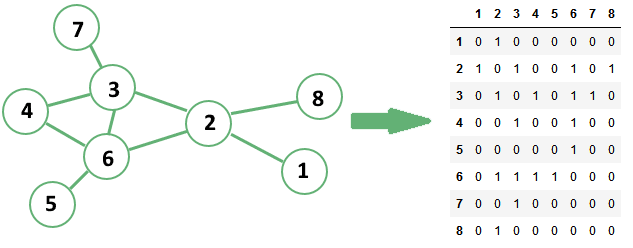
The cells in an adjacency matrix can have a value of 1 or 0 according to whether an edge exists or not between two vertices, respectively.

If the underlying graph has $N$ elements, the associated adjacency matrix will have $N\cdot N$ elements. If we define an adjacency matrix in this manner, we can then compute on it a measurement of entropy by using Shannon’s formula for randomly-distributed binary variables:

$H(x) = -\sum_{i=1}^{N^2} {p(x_i) \cdot log(p(x_i))}$

To do so we need to first convert the adjacency matrix $M$ to a random variable. We can do this by flattening the adjacency matrix. Flattening means assigning to each element $m$ with indices $(i,j)$ a unique position in a randomly-distributed variable $x = \{x_1, x_2, ... , x_{N^2}\}$ :

$x_{[N \cdot (i-1) + j]} = m_{(i,j)}$

We can then insert this variable into the formula indicated above, and thus calculate a unique value of entropy for a given graph:

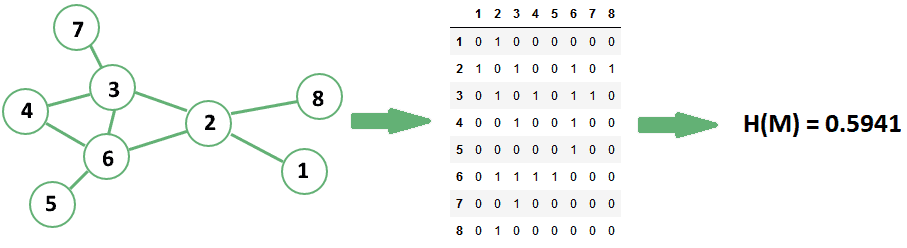
The concept of entropy in a graph is important. It’s in fact the primary reason why we can’t treat directed graphs as undirected graphs, as we’ll see shortly.

3. Directed Graphs

3.1. Definition of Directed Graphs

Directed graphs are a class of graphs that don’t presume symmetry or reciprocity in the edges established between vertices. In a directed graph, if $a$ and $b$ are two vertices connected by an edge $(a,b)$ , this doesn’t necessarily mean that an edge connecting $(b,a)$ also exists:

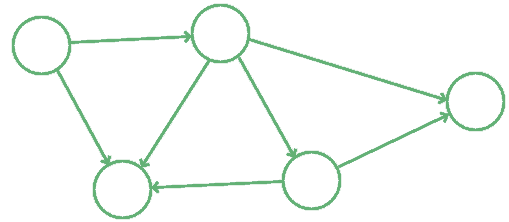
Directed edges are normally represented as arrows pointing away from the origin vertex, or tail of the arrow, and towards a destination vertex, or head of the arrow. Directed graphs are the most general kind of graphs because they don’t impose the restrictive assumption of symmetry in the relationship modeled by the edges.

3.2. Common Usages for Directed Graphs

This type of graph is also typical for the modeling of certain kinds of real-world structures. The most common directed graph is probably the genealogical or phylogenetic tree, which maps the relationship between offsprings and their parents.

In a family tree, each vertex can at the same time be a parent and an offspring in different relationships, but not simultaneously in the same one:

It wouldn’t make sense for an individual to simultaneously be the parent and the child of another individual. As a consequence, the graph which represents family trees must necessarily be a directed graph.

4. Undirected Graphs

4.1. Definition of Undirected Graphs

Undirected graphs are more specific. For them, there’s an extra assumption regarding the reciprocity in the relationship between pairs of vertices connected by an edge. If an edge $(a,b)$ exists between two vertices $a$ and $b$ , the edge $(b,a)$ also exists:

Undirected graphs are, in a sense, more restrictive than directed graphs, because they don’t allow the modeling of relationships that have a hierarchical nature. They’re however very common in practice, and many real-world relationships are best modeled by undirected graphs. This is normally the case if both vertices of an edge can be the subjects of that relationship.

For instance, the relationship “is a friend of” is a typical symmetric relationship. This is because we can assume that if “Mark is a friend of John” then it’s also true that “John is a friend of Mark.” Notice how this wasn’t the case for the relationship “is a parent of” described earlier.

4.2. Common Usages for Undirected Graphs

One of the most popular undirected graphs in computer science is the topology of connections in a computer network. The graph is undirected because we can assume that if one device is connected to another, then the second one is also connected to the first:

Other popular examples of undirected graphs include the topology of digital social networks, where each friend of someone is that someone’s friend; but also pedestrian pathways, where movement between any two intersections of paths is possible in both directions.

4.3. Symmetrical Directed Graphs Are Undirected Graphs

We can now give another definition of undirected graphs. This definition is constructed on the basis of the one for directed graphs and depends on it. A graph is undirected if its adjacency matrix is symmetric along the main diagonal.

If we use this definition, we can then find the single undirected graph that corresponds to any given directed graph. This is important because it then allows us to compare the two classes of graphs in information-theoretic terms.

Note that the opposite is not necessarily the truth, in the sense that more than one directed graph can correspond to the same undirected graph:

In our definition, two adjacency matrices $D$ and $U$ of, respectively, a directed graph and an undirected graph, correspond to one another if $D_{(i,j)}=1$ and $U_{(i,j)}=U_{(j,i)}=1$ , and also if for all $(i,j)$ such that $D_{(i,j)}=D_{(j,i)}=0$ implies that $U_{(i,j)}=U_{(j,i)}=0$ .

If the two matrices satisfy this condition, we can then use Shannon’s measure of entropy to compare the two graphs.

5. The Entropy of Directed vs Undirected Graphs

5.1. Under What Conditions Can We Compare Them?

The condition defined above and which we follow for this section is very restrictive. It implies that the two graphs we’re comparing, the directed and undirected graph, include the same vertices.

They don’t necessarily include the same edges though. Simply, the undirected graph has two directed edges between any two nodes that, in the directed graph, possess at least one directed edge.

This condition is a bit restrictive but it allows us to compare the entropy of the two graphs in general terms. We can do this in the following manner.

5.2. A Comparison of Entropy in Directed and Undirected Graphs

Let’s assume that $e$ is the number of directed edges in the directed graph $D$ . The corresponding undirected graph $U$ has a number of edges that varies between $e$ , if $D$ is symmetric, and $2e$ , if no two edges of $D$ have opposite direction.

Let’s call $d = \{d_1, d_2, ... , d_{N^2}\}$ the random binary variable associated with the adjacency matrix $D$ of the directed graph; and $u = \{u_1, u_2, ... , u_{N^2}\}$ the random binary variable associated with the adjacency matrix $U$ .

If $e$ edges of $D$ exist out of the total possible $N^2$ , then the entropy $H(d)$ of $d$ is:

$H(d) = - ( \frac{e}{N^2} \cdot log ( \frac{e}{N^2}) + (1-\frac{e}{N^2}) \cdot log (1- \frac{e}{N^2}))$

The entropy $H(u)$ of $u$ is equal to $H(d)$ if $D$ is symmetric. If $D$ has no opposite edges, though, $H(u)$ is equal to:

$H(u) = - ( \frac{2e}{N^2} \cdot log ( \frac{2e}{N^2}) + (1-\frac{2e}{N^2}) \cdot log ( 1-\frac{2e}{N^2}))$

We can consider these two cases as the extremes in a distribution of possible graph structures. Let’s now see how the two measures of entropy compare for a reference graph with $N=10$ vertices:

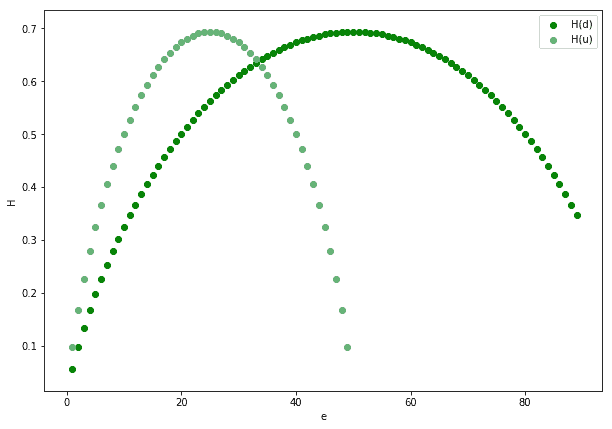
The figure above shows that, with the exception of $e = 2e = 0$ and $e = 1-2e = \frac{N^2}{3}$ , in general $H(d) \neq H(u)$ . This means that we can’t, as a general rule, treat directed graphs as undirected graphs or vice-versa. If we do, we normally pay a price in terms of their information content.

6. When to Choose One Over the Other

We can finally sum up what we learned about directed and undirected graphs. Here are some indications on how to choose which type to use:

Directed graphs are more informative than corresponding undirected graphs when the network is sparse. This means that if we treat a sparse directed graph as undirected we probably lose information
Directed graphs apply well to model relationships which are directional and not reciprocal in nature. A good example is a relationship “is a child of”, upon which we construct genealogical trees
Undirected graphs apply well to relationships for which it matters whether they exist or not, but aren’t intrinsically transitive. If, for example, we can go both ways in pedestrian paths, then we can model the pathways as an undirected graph
We can model the same system as a directed graph in some circumstances and as an undirected graph in others. For example, we can represent a family as a directed graph if we’re interested in studying progeny. If we’re studying clan affiliations, though, we can represent it as an undirected graph

Directed and undirected graphs are, by themselves, mathematical abstractions over real-world phenomena. As a consequence, a programmer should choose carefully which one to apply to a problem. The graph needs to correspond to the type of relationships which we model: undirected if it’s reciprocal, directed otherwise.

7. Conclusions

In this article, we’ve seen what’s the difference between directed and undirected graphs. Directed graphs have edges that are directional and not necessarily reciprocal. If a vertex in a directed graph is connected to another, that doesn’t necessarily mean that the second is also connected to the first.

Undirected graphs are more restrictive kinds of graphs. They represent only whether or not a relationship exists between two vertices. They don’t however represent a distinction between subject and object in that relationship.

One type of graph can sometimes be used to approximate the other. When we do, though, there’s often a cost to pay in terms of information content.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex