Methods of Depth First Traversal and Their Applications

1. Introduction

Tree traversal is a process of visiting nodes of a tree exactly once. There are many ways of traversing trees, and they’re usually classified based on the order that the traversal occurs. They can also be broadly categorized based on the direction of traversal as depth-first (vertical) or breadth-first (horizontal) traversal.

In this tutorial, we’ll take a closer look at three types of depth-first traversal: in-order, post-order and pre-order. We’ll be applying what we learn on a binary tree because they’re easier to represent and the examples will be easier to trace. However, we can apply these concepts to any type of graph.

2. Our Binary Tree Example

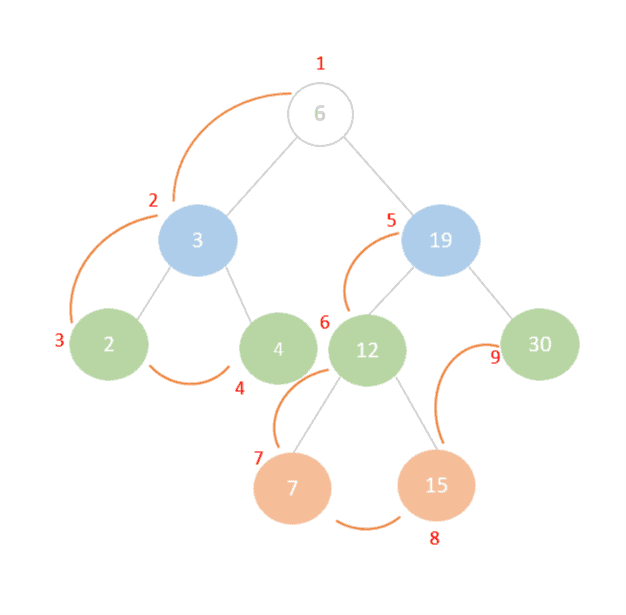
The image below is an example of a Binary Search Tree. In the following sections, we’ll be demonstrating the different methods of traversal on this tree:

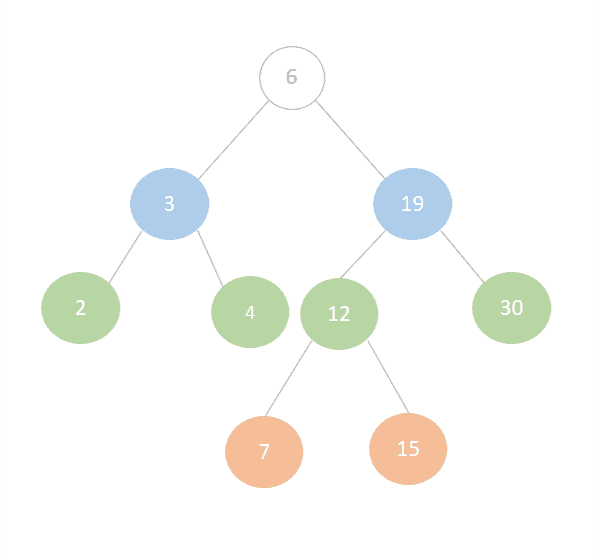
Bear in mind that if we were working with graphs, we could pick any node to start with. However, when we’re working with binary trees, we always start traversing from the root, in this case, 6.

3. In-order Traversal (LNR)

In-order traversal is given the acronym of LNR which stands for Left, Node, Right as an indication of the order in which we traverse a tree.

To perform in-order traversal, we follow these steps recursively:

1. Traverse the left sub-tree
2. Traverse the root node
3. Traverse the right sub-tree

Starting from the root (6) we check:

• Does it have a left child? It does, so we check the left child (3) and ask does it have a left child? Yes, it does, but that child (2) doesn’t have a left child so we can traverse it
• As this is in-order the next node we traverse is the root of (2) which is node (3) followed by the right child (4)
• Now, since (4) has no children of its own to traverse we’ve finished traversing the left sub-tree and we can continue to traverse the root of the tree (6) followed by its right sub-tree

To traverse the right sub-tree we check:

• If the node (19) has a left node, we’ll traverse it; it does, and its left node (12) has a left node (7) which has no children to traverse. So we traverse (7) and then its root (12) and then the right node (15).
• Finally, we go back to the node (19) after we finished processing its left sub-tree and traverse it followed by its right node (30).

In this way, we’ve traversed the nodes of the tree completely using in-order traversal in the same way that is displayed in the image below. Note the numbers in red mark the order in which the nodes were traversed:

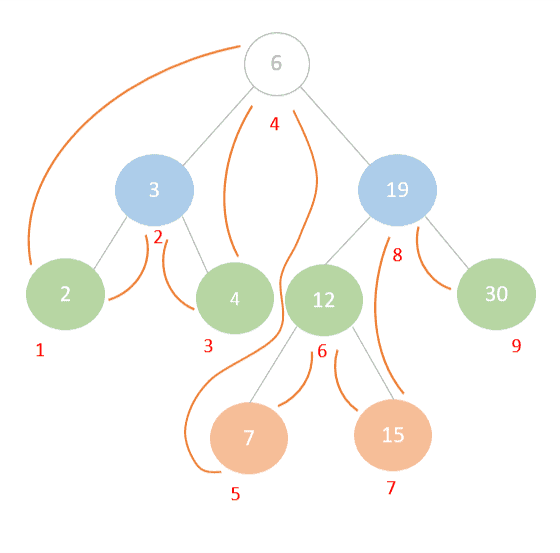
One of the most popular uses of in-order traversal is to retrieve the sorted contents of a Binary Search Tree in ascending order. Alternatively, to retrieve the items in descending order we can reverse the process by starting from the right sub-tree and ending with the left. This is known as Reverse In-order Traversal.

4. Post-order Traversal (LRN)

With post-order traversal (left, right, node) we take a different order and instead follow these steps recursively starting from the root:

1. Traverse the left sub-tree
2. Traverse the right sub-tree
3. Traverse the root node

Let’s traverse our same tree but this time let’s do it using post-order traversal:

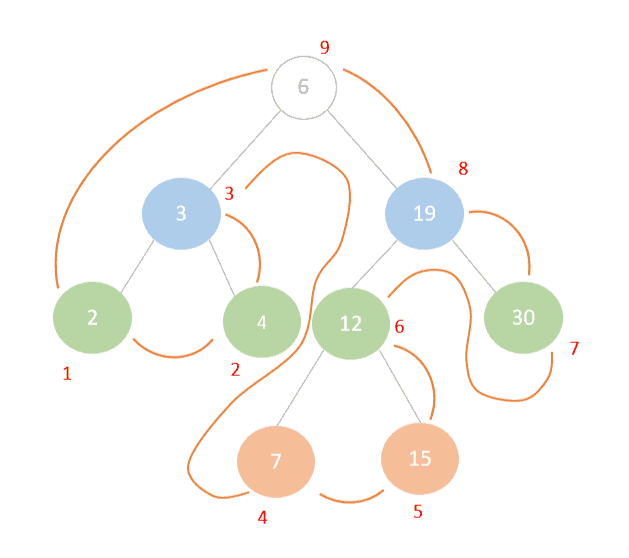
Similar to in-order traversal, we start by looking at the root of the tree and checking its left-most node until we find the left leaf node (2) that we can start our traversing from. Once we’ve traversed the (2) we traverse its right sibling node (4) and then its root (3). In doing so, we’ve finished traversing the left subtree and we can move onto the right sub-tree in the same way, leaving the root of the tree to last.

Post-order traversal has useful applications in some languages which don’t have built-in garbage collection such as C and C++. To free an object from memory, we must visit its children first and free them from memory before visiting their parents. If we don’t do that, we’ll have a case that we know as a dangling pointer. We can also use post-order traversal when we need to delete nodes from a binary search tree. We must first traverse and delete the leaves before the roots.

Post-order traversal was also quite popular at some point as part of a method of expression evaluation known as Reverse Polish Notation (RPN) or postfix notation. RPN is used to express mathematical formulas in such a way that there is no need to use brackets to keep the order of precedence. For example, using RPN we could represent this mathematical expression:

Like this:

This meant simpler computation and was easier for machines to interpret. Historically, some Hewlett-Packard calculators and languages such as PostScript and Forth made use of RPN and became quite popular. Nowadays, RPN has very specific use cases in areas related to parsing mathematical expressions. We can construct the RPN by performing a post-order traversal of the syntax tree.

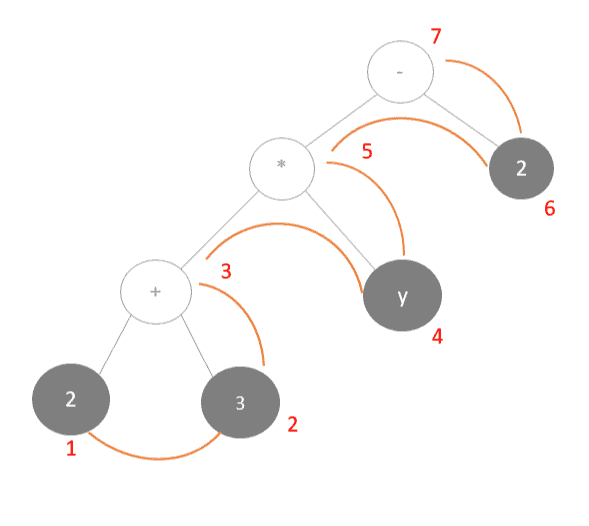
Let’s take a look at a small example of how this would work using our mathematical expression above.

First, we would represent the mathematical expression as an expression tree:

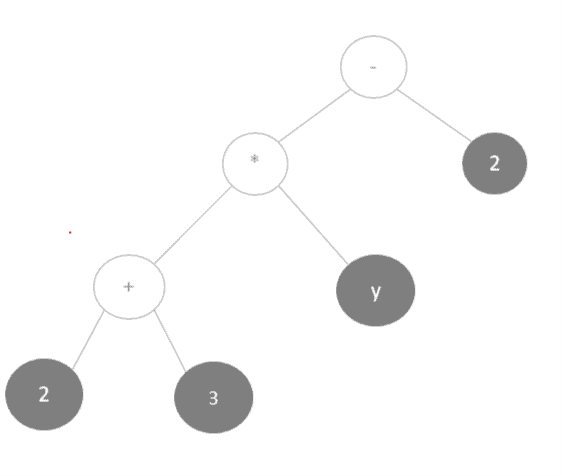
Next, we’d perform a post-order traversal of the tree to get the postfix notation for this expression:

5. Pre-order Traversal (NLR)

Finally, let’s learn about pre-order traversal. As the acronym suggests, pre-order traversal traverses the root node first then the left and right subtrees respectively. This means we would traverse the tree by taking these steps:

1. Traverse the root node
2. Traverse the left sub-tree
3. Traverse the right sub-tree

Take a look at how this would work out with our example binary search tree:

With this method, we’ll start by traversing the root node (6), then move on to its left sub-tree. The root of the left sub-tree is (3), so after we traverse it we go on to traverse its left child (2) followed by its right child (4) thereby finishing the traversal of the left sub-tree. Finally, we traverse the right sub-tree in a similar manner starting with the root node (19) and ending with its right child (30).

Pre-order traversal is useful when we’re searching for an element within a binary search tree. We can use the root nodes value to determine if we need to search the right or left subtree next. Moreover, databases typically make use of pre-order traversal to traverse B-tree indexes during search operations.

Pre-order traversal also has applications in what is known as topological sorting. Assuming that a node is a pre-requisite or a dependency of its children, a pre-order traversal on a topologically ordered tree is useful for listing the dependency before the dependants. Topological ordering has use cases in dynamic linking of programs and resolving dependencies as well as processor scheduling.

One specific example which uses this is the Linux makefile utility.

6. Conclusion

To conclude, we’ve covered some depth-first traversal methods and learned about their applications in the real world. Although we discussed these methods in the context of binary trees, we can also use these concepts for traversing graphs.

If we’re ready to jump into the implementation details, we can now learn more about how to implement some of these methods in Java.