1. Overview
In this tutorial, we’ll discuss finding the shortest path in a graph visiting all nodes.
First, we’ll define the problem and provide an example that explains it. Then, we’ll discuss two different approaches to solve this problem.
2. Defining the Problem
Suppose we have a graph, , that contains
nodes numbered from
to
. In addition, we have
edges that connect these nodes. Each of these edges has a weight associated with it, representing the cost to use this edge.
Our task is to find the shortest path that goes through all nodes in the given graph.
Recall that the shortest path between two nodes and
is the path that has the minimum cost among all possible paths between
and
.
In this task, we look for all the paths that cover all possible starting and ending nodes. Besides, we can visit the same node more than once. Let’s look at an example for better understanding.
Suppose we have the following graph:
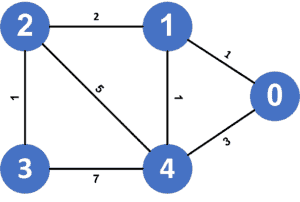
As we can see, there’re many paths that go through all nodes in the given graph, but the shortest path among them , and it has a cost equal to
; therefore, the shortest path in the given graph visiting all nodes has a cost equal to
.
3. Brute Force Approach
3.1. Main Idea
The main idea here is to generate all the possible paths and get the one that has the minimum cost.
Firstly, we’ll generate all the possible permutations of nodes. Each permutation will represent the order of visiting nodes in the graph. A path’s cost will be equal to the sum of all shortest paths between every two consecutive nodes.
Secondly, we’ll calculate the shortest path between every two consecutive nodes using the Floyd-Warshall algorithm. Recall that the Floyd-Warshall algorithm calculates the shortest path between all pairs of nodes inside a graph.
Finally, the shortest path visiting all nodes in a graph will have the minimum cost among all possible paths.
3.2. Implementation
Let’s take a look at the implementation:
algorithm BruteForceApproach(V, G):
// INPUT
// V = the number of nodes in the graph
// G = the graph stored as an adjacency list
// OUTPUT
// Returns the shortest path visiting all nodes in G
answer <- infinity
distance <- Calculate_Floyd_Warshall(G) // a matrix
permutations <- Calculate_Permutations()
for permutation in permutations:
cost <- 0
previous <- permutation[0]
for node in permutation:
cost <- cost + distance[previous, node]
previous <- node
if cost < answer:
answer <- cost
return answerInitially, we declare an array called , which stores the shortest path between every pair of nodes in the given graph using the Floyd-Warshall algorithm.
Next, we generate all the possible permutation which represent all the possible paths we could follow. Then for each permutation, we’ll calculate the cost of it by adding the length of the shortest path between every two consecutive nodes; after calculating the cost of the current permutation, we’ll check if the is less than the
value, then we’ll update the
.
Finally, we return , which stores the cost of the shortest path visiting all nodes in the given graph.
3.3. Complexity
The time complexity here is . Let’s examine the reason behind this complexity.
First, the Floyd-Warshall algorithm has complexity . Next, the number of all different permutations of
nodes is equal to the factorial of
, and for each permutation, we calculate its cost by passing through it, so it’s
.
Therefore, the total complexity will be .
4. Dijkstra Approach
4.1. Main Idea
In this approach, we’ll use a modified version of the Dijkstra algorithm. For each state, we need to keep track of all the visited nodes besides the current one. So, to get all the visited nodes in each state, we’ll represent them as bitmask where each bit that’s turned on means that we’ve visited this node before.
In the end, our answer we’ll be the minimum value among all nodes’ values that have a bitmask full of ones (visited all nodes).
4.2. Implementation
Let’s take a look at the implementation:
algorithm DijkstraApproach(V, G):
// INPUT
// V = the number of nodes in the graph
// G = the graph stored as an adjacency list
// OUTPUT
// Returns the shortest path visiting all nodes
cost <- a matrix whose all entries are infinity
priority_queue <- make an empty priority queue
for node from 0 to V-1:
priority_queue.add(node, 2^node)
cost[node, 2^node] <- 0
while priority_queue is not empty:
current <- priority_queue.front().node
mask <- priority_queue.front().bitmask
priority_queue.pop()
for child in G[current]:
add <- weight(current, child)
if cost[child, mask or 2^child] > cost[current, mask] + add:
priority_queue.add(child, mask or 2^child)
cost[child][mask or 2^child] <- cost[current][mask] + add
answer <- infinity
for node from 0 to V-1:
answer <- min(answer, cost[node, 2^V - 1])
return answerInitially, we declare an array called , which stores the shortest path to some node visiting a subset of nodes. We also declare a priority queue that stores a node and a bitmask. The bitmask represents all visited nodes to get to this node. This priority queue will sort states in acceding order according to the cost of the state.
Next, we try to start the shortest path from each node by adding each node to the priority queue and turning their bit on. Then, we run the Dijkstra algorithm.
We iterate over the children nodes of the node. For each
, we check if the
value of it visiting a specific subset of nodes greater than the current
plus the weight of the edge that connects the
node with the
. In this case, we need to update the
value of the
node. Also, we add the
and the current
bitwise-or
to the priority queue. This mask means that we turn the bit of the
node on.
Finally, our answer will be the minimum value among all the nodes cost visiting all nodes.
4.3. Complexity
The time complexity here is , where
is the number of nodes and
is the number of all possible subset of nodes, and
for adding each state to the priority queue.
5. Conclusion
In this article, we presented the problem of finding the shortest path visiting all nodes. We explained the main ideas behind two different approaches to solving this problem and walked through their implementation.