Finding the Parent of a Node in a Binary Search Tree with Java

1. Introduction

A Binary Search Tree (BST) is a data structure that helps us efficiently solve real-world problems.

In this post, we’ll look at how to solve the problem of finding the parent of a node in a BST.

2. What Is a Binary Search Tree?

A BST is a tree where each node points to at most two nodes, often called left and right children. Additionally, each node’s value is greater than the left child and smaller than the right child.

For instance, let’s picture three nodes, A=2, B=1, and C=4. Hence, one possible BST has A as the root, B as its left child, and C as its right child.

In the next sections, we’ll use a BST structure implemented with a default insert() method to exercise the problem of finding the parent of a node.

3. The Parent of a Node in a Binary Search Tree

In the following sections, we’ll describe the problem of finding a node’s parent in a BST and exercise a few approaches to solve it.

3.1. Description of the Problem

As we’ve seen throughout the article, a given node of a BST has pointers to its left and right children.

For instance, let’s picture a simple BST with three nodes:

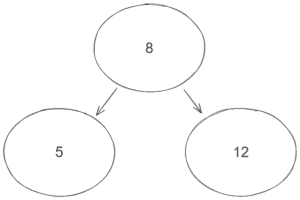
The node 8 contains two children, 5 and 12. Hence, node 8 is the parent of nodes 5 and 12.

The problem consists of finding the parent of any given node value. In other words, we must find the node where any of its children equals the target value. For instance, in the BST of the image above, if we input 5 into our program, we expect 8 as output. If we input 12, we also expect 8.

The edge cases for this problem are finding the parent for either the topmost root node or a node that doesn’t exist in the BST. In both cases, there’s no parent node.

3.2. Test Structure

Before diving into the various solutions, let’s first define a basic structure for our tests:

class BinaryTreeParentNodeFinderUnitTest {

    TreeNode subject;

    @BeforeEach
    void setUp() {
        subject = new TreeNode(8);
        subject.insert(5);
        subject.insert(12);
        subject.insert(3);
        subject.insert(7);
        subject.insert(1);
        subject.insert(4);
        subject.insert(11);
        subject.insert(14);
        subject.insert(13);
        subject.insert(16);
    }
}

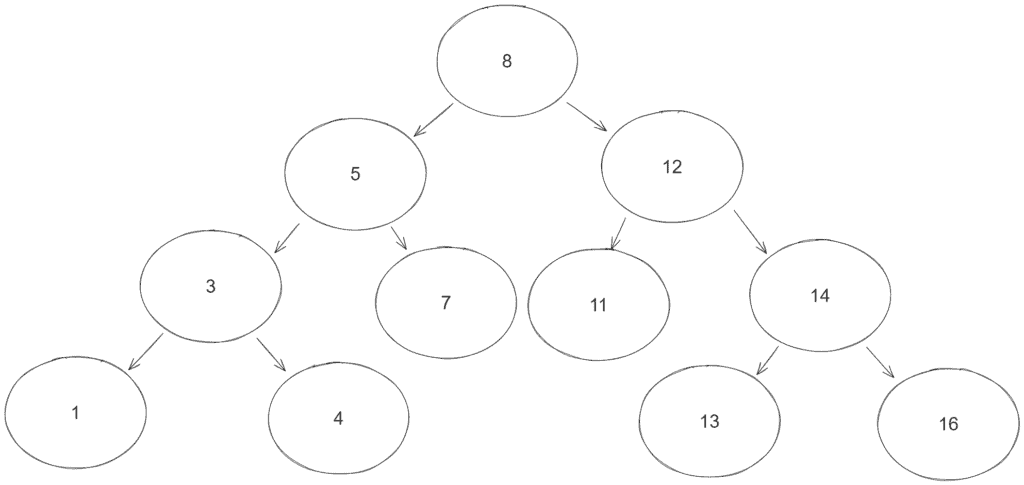
The BinaryTreeParentNodeFinderUnitTest defines a setUp() method that creates the following BST:

4. Implementing a Recursive Solution

The straightforward solution to the problem is using recursion to traverse the tree and early return the node where any of its children is equal to the target value.

Let’s first define a public method in the TreeNode class:

TreeNode parent(int target) throws NoSuchElementException {
    return parent(this, new TreeNode(target));
}

Now, let’s define the recursive version of the parent() method in the TreeNode class:

TreeNode parent(TreeNode current, TreeNode target) throws NoSuchElementException {
    if (target.equals(current) || current == null) {
        throw new NoSuchElementException(format("No parent node found for 'target.value=%s' " +
            "The target is not in the tree or the target is the topmost root node.",
            target.value));
    }

    if (target.equals(current.left) || target.equals(current.right)) {
        return current;
    }

    return parent(target.value < current.value ? current.left : current.right, target);
}

The algorithm first checks if the current node is the topmost root node or the node doesn’t exist in the tree. In both situations, the node doesn’t have a parent, so we throw a NoSuchElementException.

Then, the algorithm checks if any current node children equal the target. If so, the current node is the parent of the target node. Thus, we return current.

Finally, we traverse the BST using recursive calls to left or right, depending on the target value.

Let’s test our recursive solution:

@Test
void givenBinaryTree_whenFindParentNode_thenReturnCorrectParentNode() {
    assertThrows(NoSuchElementException.class, () -> subject.parent(1231));
    assertThrows(NoSuchElementException.class, () -> subject.parent(8));
    assertEquals(8, subject.parent(5).value);
    assertEquals(5, subject.parent(3).value);
    assertEquals(5, subject.parent(7).value);
    assertEquals(3, subject.parent(4).value);
    // assertions for other nodes
}

In the worst-case scenario, the algorithm executes at most n recursive operations with O(1) cost each to find the parent node, where n is the number of nodes in the BST. Thus, it is O(n) in time complexity. That time falls to O(log n) in well-balanced BSTs since its height is always at most log n.

Additionally, the algorithm uses heap space for the recursive calls. Hence, in the worst-case scenario, the recursive calls stop when we find a leaf node. Therefore, the algorithm stacks at most h recursive calls, which makes it O(h) in space complexity, where h is the BST’s height.

5. Implementing an Iterative Solution

Pretty much any recursive solution has an iterative version. Particularly, we can also find the parent of a BST using a stack and while loops instead of recursion.

For that, let’s add the iterativeParent() method to the TreeNode class:

TreeNode iterativeParent(int target) {
    return iterativeParent(this, new TreeNode(target));
}

The method above is simply an interface to the helper method below:

TreeNode iterativeParent(TreeNode current, TreeNode target) {
    Deque <TreeNode> parentCandidates = new LinkedList<>();

    String notFoundMessage = format("No parent node found for 'target.value=%s' " +
        "The target is not in the tree or the target is the topmost root node.",
        target.value);

    if (target.equals(current)) {
        throw new NoSuchElementException(notFoundMessage);
    }

    while (current != null || !parentCandidates.isEmpty()) {

        while (current != null) {
            parentCandidates.addFirst(current);
            current = current.left;
        }

        current = parentCandidates.pollFirst();

        if (target.equals(current.left) || target.equals(current.right)) {
            return current;
        }

        current = current.right;
    }

    throw new NoSuchElementException(notFoundMessage);
}

The algorithm first initializes a stack to store parent candidates. Then it mostly depends on four main parts:

1. The outer while loop checks if we are visiting a non-leaf node or if the stack of parent candidates is not empty. In both cases, we should continue traversing the BST until we find the target parent.
2. The inner while loop checks again if we are visiting a non-leaf node. At that point, visiting a non-leaf node means we should traverse left first since we use an in-order traversal. Thus, we add the parent candidate to the stack and continue traversing left.
3. After visiting the left nodes, we poll a node from the Deque, check if that node is the target’s parent, and return it if so. We keep traversing to the right if we don’t find a parent.
4. Finally, if the main loop completes without returning any node, we can assume that the node doesn’t exist or it’s the topmost root node.

Now, let’s test the iterative approach:

@Test
void givenBinaryTree_whenFindParentNodeIteratively_thenReturnCorrectParentNode() {
    assertThrows(NoSuchElementException.class, () -> subject.iterativeParent(1231));
    assertThrows(NoSuchElementException.class, () -> subject.iterativeParent(8));
    assertEquals(8, subject.iterativeParent(5).value);
    assertEquals(5, subject.iterativeParent(3).value);
    assertEquals(5, subject.iterativeParent(7).value);
    assertEquals(3, subject.iterativeParent(4).value);
    
    // assertion for other nodes
}

In the worst case, we need to traverse the entire o tree to find the parent, which makes the iterative solution O(n) in space complexity. Again, if the BST is well-balanced, we can do the same in O(log n).

When we reach a leaf node, we start polling elements from the parentCandidates stack. Hence, that additional stack to store the parent candidates contains, at most, h elements, where h is the height of the BST. Therefore, it also has O(h) space complexity.

6. Creating a BST With Parent Pointers

Another solution to the problem is to modify the existing BST data structure to store each node’s parent.

For that, let’s create another class named ParentKeeperTreeNode with a new field called parent:

class ParentKeeperTreeNode {

    int value;
    ParentKeeperTreeNode parent;
    ParentKeeperTreeNode left;
    ParentKeeperTreeNode right;

    // value field arg constructor

    // equals and hashcode
}

Now, we need to create a custom insert() method to also save the parent node:

void insert(ParentKeeperTreeNode currentNode, final int value) {
    if (currentNode.left == null && value < currentNode.value) {
        currentNode.left = new ParentKeeperTreeNode(value);
        currentNode.left.parent = currentNode;
        return;
    }

    if (currentNode.right == null && value > currentNode.value) {
        currentNode.right = new ParentKeeperTreeNode(value);
        currentNode.right.parent = currentNode;
        return;
    }

    if (value > currentNode.value) {
        insert(currentNode.right, value);
    }

    if (value < currentNode.value) {
        insert(currentNode.left, value);
    }
}

The insert() method also saves the parent when creating a new left or right child for the current node. In that case, since we are creating a new child, the parent is always the current node we are visiting.

Finally, we can test the BST version that stores parent pointers:

@Test
void givenParentKeeperBinaryTree_whenGetParent_thenReturnCorrectParent() {
    ParentKeeperTreeNode subject = new ParentKeeperTreeNode(8);
    subject.insert(5);
    subject.insert(12);
    subject.insert(3);
    subject.insert(7);
    subject.insert(1);
    subject.insert(4);
    subject.insert(11);
    subject.insert(14);
    subject.insert(13);
    subject.insert(16);

    assertNull(subject.parent);
    assertEquals(8, subject.left.parent.value);
    assertEquals(8, subject.right.parent.value);
    assertEquals(5, subject.left.left.parent.value);
    assertEquals(5, subject.left.right.parent.value);

    // tests for other nodes
}

In that type of BST, we calculate parents during node insertion. Thus, to verify the results, we can simply check the parent reference in each node.

Therefore, instead of calculating the parent() of each given node in O(h), we can get it immediately by reference in O(1) time. Additionally, each node’s parent is just a reference to another existing object in memory. Thus, the space complexity is also O(1).

That version of BST is helpful when we often need to retrieve the parent of a node since the parent() operation is well-optimized.

7. Conclusion

In that article, we saw the problem of finding the parent of any given node of a BST.

We’ve exercised three solutions to the problem with code examples. One uses recursion to traverse the BST. The other uses a stack to store parent candidates and traverse the BST. The last one keeps a parent reference in each node to get it in constant time.