1. Introduction
In this article, we’ll briefly look at binary trees and review some useful applications of this data structure.
A binary tree is a tree data structure comprising of nodes with at most two children i.e. a right and left child. The node at the top is referred to as the root. A node without children is known as a leaf node. Most applications use different variants of binary trees such as tries, binary search trees, and B-trees.
In computing, binary trees are mainly used for searching and sorting as they provide a means to store data hierarchically. Some common operations that can be conducted on binary trees include insertion, deletion, and traversal.
2. Routing Tables
A routing table is used to link routers in a network. It is usually implemented with a trie data structure, which is a variation of a binary tree. The tree data structure will store the location of routers based on their IP addresses. Routers with similar addresses are grouped under a single subtree.
To find a router to which a packet must be forwarded, we need to traverse the tree using the prefix of the network address to which a packet must be sent. Afterward, the packet is forwarded to the router with the longest matching prefix of the destination address.
3. Decision Trees
Binary trees can also be used for classification purposes. A decision tree is a supervised machine learning algorithm. The binary tree data structure is used here to emulate the decision-making process.
A decision tree usually begins with a root node. The internal nodes are conditions or dataset features. Branches are decision rules while the leave nodes are the outcomes of the decision.
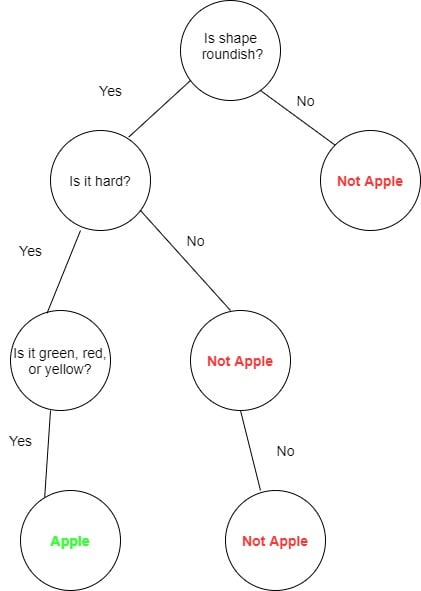
For example, suppose we want to classify apples. The decision tree for this problem will be as follows:
4. Expression Evaluation
Another useful application of binary trees is in expression evaluation. In mathematics, expressions are statements with operators and operands that evaluate a value. The leaves of the binary tree are the operands while the internal nodes are the operators.
The expression is evaluated by applying the operator(s) in the internal node to the operands in the leaves.
5. Sorting
Binary search trees, a variant of binary trees are used in the implementation of sorting algorithms to order items. A binary search tree is simply an ordered or sorted binary tree such that the value in the left child is less than the value in the parent node. At the same time, the values in the right node are greater than the value in the parent node.
To complete a sorting procedure, the items to be sorted are first inserted into a binary search tree. To retrieve the sorted items, the tree is traversed using in-order traversal.
For more details on sorting in a binary tree, check out our article on sorting elements in binary trees.
6. Indices for Databases
In database indexing, B-trees are used to sort data for simplified searching, insertion, and deletion. It is important to note that a B-tree is not a binary tree, but can become one when it takes on the properties of a binary tree.
The database creates indices for each given record in the database. The B-tree then stores in its internal nodes, references to data records with the actual data records in its leaf nodes. This provides sequential access to data in the databases.
For further details about how B-trees are used in databases, check out our article on B-trees in the context of databases.
7. Data Compression
In data compression, Huffman coding is used to create a binary tree capable of compressing data. Data compression is the processing of encoding data to use fewer bits. Given a text to compress, Huffman coding builds a binary tree and inserts the encodings of characters in the nodes based on their frequency in the text.
The encoding for a character is obtained by traversing the tree from its root to the node. Frequently occurring characters will have a shorter path as compared to less occurring characters. This is done to reduce the number of bits for frequent characters and ensure maximum data compression.
For more details on how Huffman code is generated, check out our article on Queues.
8. Conclusion
In this article, we have reviewed the application of the binary tree data structure in real-world applications.