1. Overview
In this tutorial, we’re going to look at the differences between important data structures which are trees and graphs. With them, we can solve many complex problems efficiently.
2. Trees
We can define the tree data structure as a collection of nodes recursively. Each node in the tree structure is a data structure that has a value and a list of references to nodes. As we can see in the figure below, each circle shows a node, or vertex, in the tree. We call the lines between nodes edges. This tree includes six nodes with as its root:
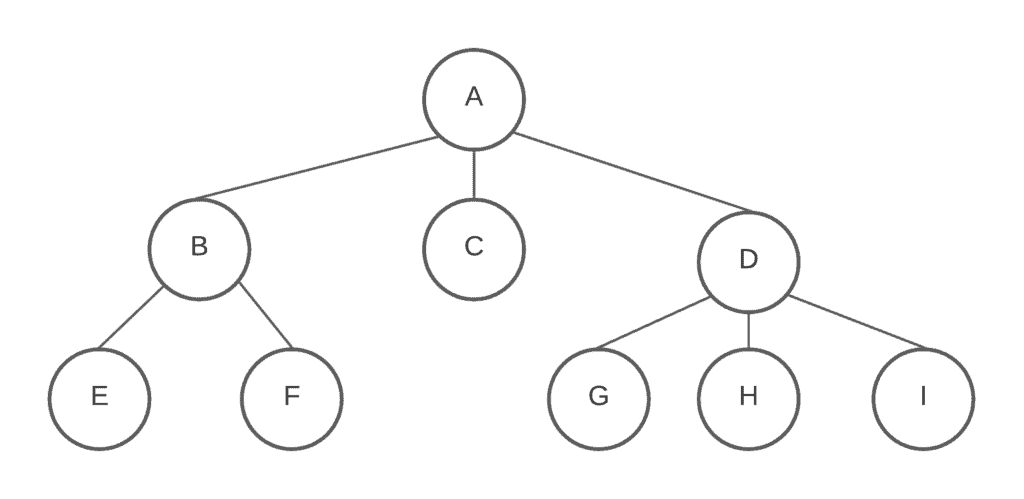
is the parent of
and
.
and
are the children of node
, so they are siblings. Because they have the same parent node which is
. As we guess, there is an obvious hierarchy between nodes. While node
is the ancestor of all the nodes in the tree, child
and child
have different descendants.
The figure above shows a structure that is not a binary tree. It’s a generic tree which is a non-binary and unsorted tree.
We generally use trees to represent relationships. Unlike arrays and linked lists, trees are hierarchical and non-linear structures. For example, while trying to find possible situations in a strategy game like chess, we use decision trees. There are also so many other real-world examples of tree data structures.
2.1. The Binary Tree
A binary tree is a restricted version of a tree data structure. In a binary tree, each node has at most two children. At this point, we can ask ourselves: are these tree structures really similar to the trees in nature? The answer is not quite because in nature trees grow with their roots in the ground and their leaves in the air. Computer scientists describe tree data structures with the root at the top and the leaves at the bottom:
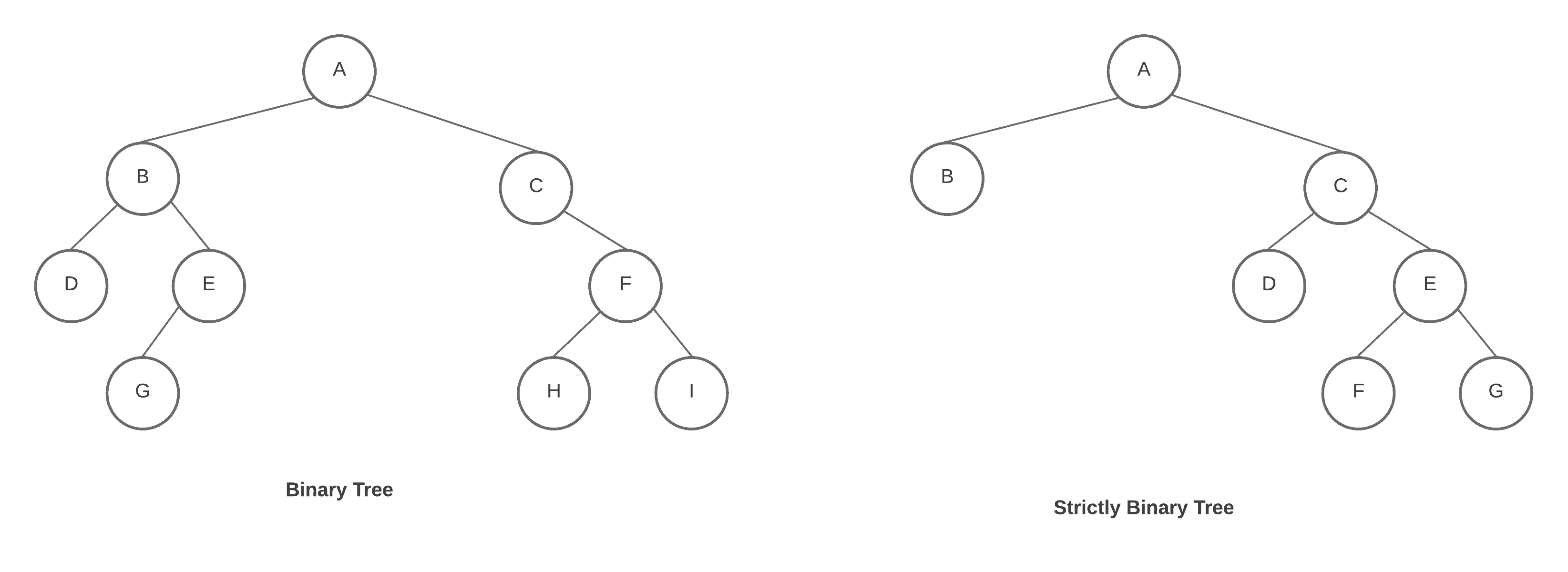
We call a tree, strictly binary tree, every non-leaf node in a binary tree has nonempty left and right subtrees as can be seen in the figure above. A strictly binary tree that has leaves always contains
nodes.
The root of the tree has level 0, and the level of any other node in the tree is one more than the level of its parent. For example, in the binary tree (left one) of the figure above, node is at level 3. The depth of a binary tree is the maximum level of any leaf in the tree.
2.2. The Binary Search Tree (BST)
A binary search tree is a restricted version of binary data structure. Its internal nodes store a key greater than all the keys in the node’s left subtree and less than in its right subtree:
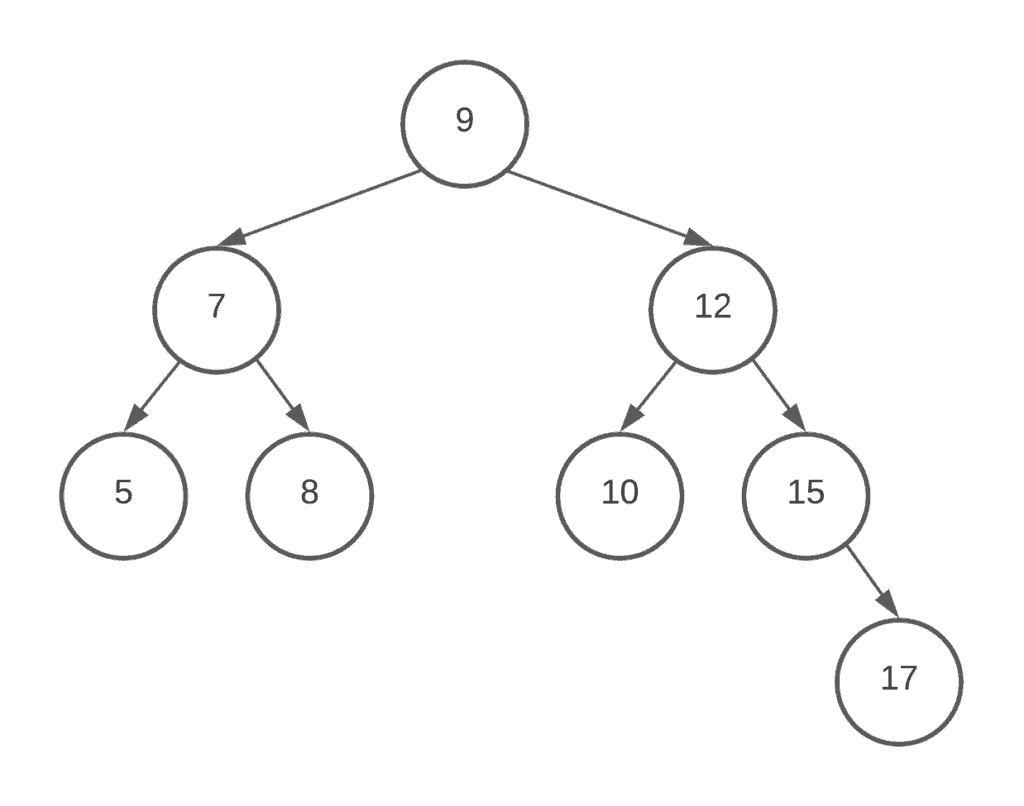
3. Graphs
A graph is a data structure that has a set of vertices, or nodes, and edges like a tree. However, there are no such restrictions in graphs. They are like extended versions of trees or in other words, actually, trees are the restricted version of graphs. The graph in the figure below shows the one-way routes among eleven cities:
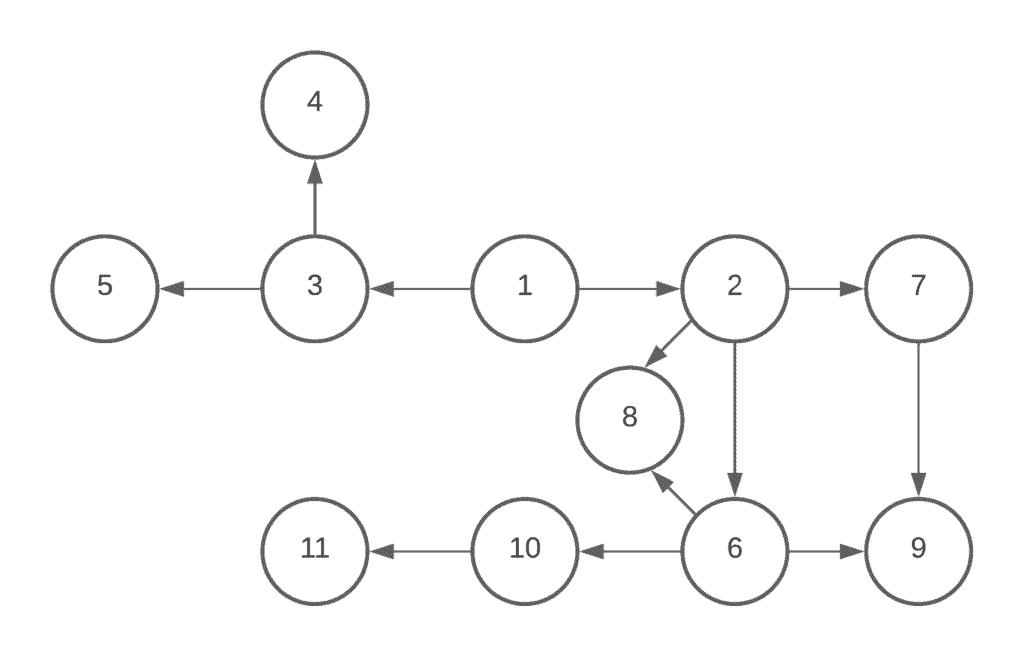
When there is an edge between two vertices we call them adjacent vertices in a graph data structure. There are two ways to implement the graph which are adjacent matrix and adjacency list.
Graphs can be connected, disconnected, and complete. We can also classify them as weighted and unweighted graphs, and directed and undirected graphs. The kind of graph is closely related to the problem that we focus on. For example, if we try to find the minimum cost between cities where we have the different distances for each route, in that case, it can be more suitable to use weighted graphs.
4. Differences Between Tree and Graph Data Structure
Even though a tree is a sort of a graph, there are some key differences between a tree and graph data structure:
- While a tree has a hierarchical structure, a graph has a network model.
- In a tree there exists only one route between any two vertices, however, we can have a graph that can have unidirectional routes between the nodes.
- Trees don’t include loops while graphs can have loops and even self-loops.
- Trees have simple structures, however, graphs can have more complicated structures since they can have loops.
- If we have a
number of nodes in a tree, we’ll have
edges. In the graph, there is no such relation between edges and nodes. It totally depends on the graph.
- In a tree, we have exactly one root node. However, in a graph, there is no concept of a root node.
- We can traverse a tree using in-order, pre-order, or post-order traversal methods. For graph traversal, we use Breadth-First Search (BFS), and Depth-First Search (DFS).
5. Conclusion
In this article, we’ve briefly explained the tree and graph data structure. We’ve also focused on key differences between them. These two concepts are not only important for computer science, actually have a really crucial role in mathematic.