Difference Between Tree Depth and Height

1. Introduction

A tree’s height and depth are important attributes to consider in complexity analysis as well as for numerous algorithms. In this tutorial, we’ll try to show the difference between these two attributes.

2. Problem Explanation

For each node in a tree, we can define two features: height and depth. A node’s height is the number of edges to its most distant leaf node. On the other hand, a node’s depth is the number of edges back up to the root. So, the root always has a depth of while leaf nodes always have a height of . And if we look at the tree as a whole, its depth and height are both the root height.

3. Flowchart

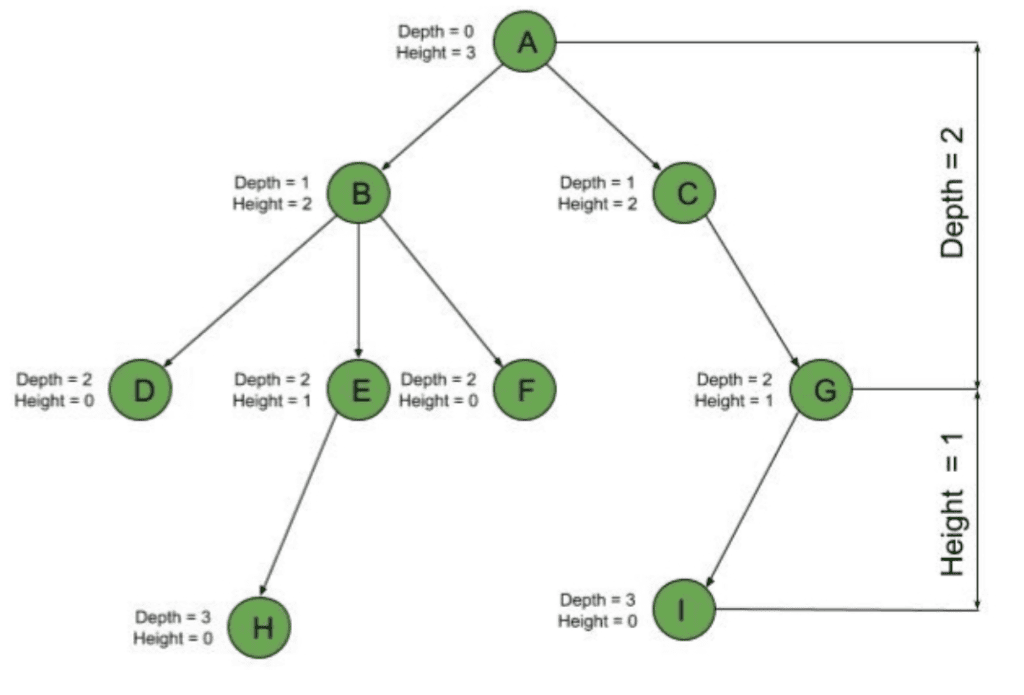
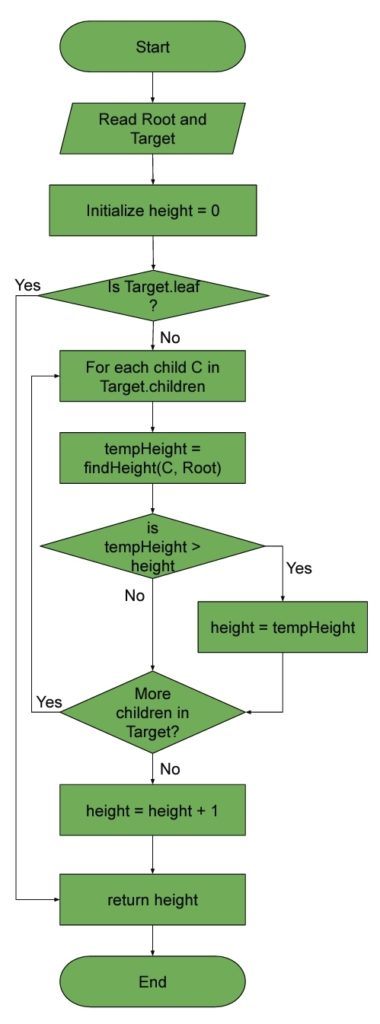
Calculating the height or depth for any node can be done using breadth-first search (BFS). But, we’re going to leave the general case for a future post. Simply put, we can find the height recursively by setting the height of the node as the maximum height of its children :

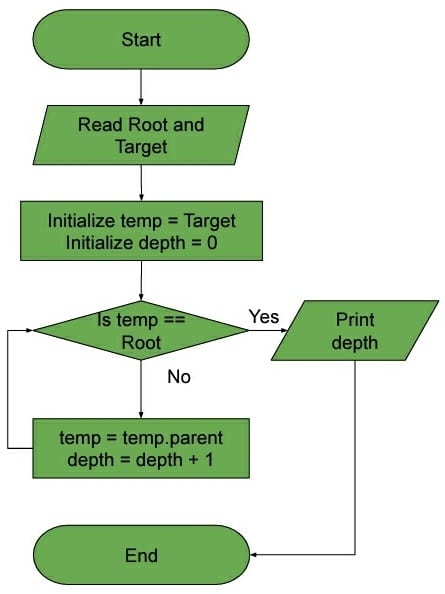
For depth, if we assume that each node in the tree stores its parent node, we can traverse from our target node up to the root, counting the edges along the way:

algorithm findHeight(Target, Root):
    // INPUT
    //   Target =  Target Node
    //   Root = Tree Root 
    // OUTPUT
    //   Target Node Height
    height <- 0
    for C in Target.children:
        tempHeight <- findHeight(C, Root)
        if tempHeight > height:
            height <- tempHeight
    height <- height + 1
    return height

A leaf node has no children, and its height is zero. With depth, we traverse upwards:

algorithm findDepth(Target, Root):
    // INPUT
    //   Target =  Target Node
    //   Root = Tree Root 
    // OUTPUT
    //   Target Node Depth
    depth <- 0
    temp <- Target
    while root != temp:
        temp <- temp.parent
        depth <- depth + 1
    return depth

5. Complexity

We can also compare their complexities. Since we used BFS for finding the height, the complexity is where n is the number of nodes in the tree. As for the depth algorithm, we iterate over the edges from the target node up to the root. Thus, we can easily see that the time complexity for finding the depth of a node is , and the worst case will be . Also, the space complexity is for finding height and depth. In the case of finding the height, we need to allocate memory for the BFS queue (which is allocated automatically in the recursive solution). And we need to allocate space for the parents in the case of finding the depth.

6. Conclusion

In this short article, we showed the difference between tree height and depth. To do this, we examined approaches for calculating them and compared their space-time complexities.