1. Introduction
In this tutorial, we’ll explain the way how to validate neural networks or any other machine learning model. First, we’ll briefly introduce the term neural network. After that, we’ll describe what does validation means and different strategies for validation. Finally, we’ll explain a particular type of validation, called k-fold cross-validation, with some modifications.
In general, validation is a critical step in building a machine learning system since the validity of results directly depends on it.
2. Neural Networks
Neural networks are algorithms explicitly created as an inspiration for biological neural networks. The basis of neural networks is neurons interconnected according to the type of network. Initially, the idea was to create an artificial system that would function just like the human brain.
There are many types of neural networks, but they roughly fall into three main classes:
For the most part, the difference between them is the type of neurons that form them and how the information flows through the network. To test neural network predictions, we need to use appropriate methods that we’ll explain below.
3. Validation
After we train the neural network and generate results with a test set, we need to check how correct they are.
3.1. Machine Learning Metrics
Usually, in neural networks or machine learning methods, we measure the quality of the method using a metric that represents the error or correctness of the solution. Errors are used for problems such as regression, while correctness is more common for classification problems. Thus, the most commonly used metrics in classification problems are:
If a classification model, besides predicted class, outputs probability or confidence of the prediction, we can use measures:
- AUC
- Cross-entropy
Also, the most used metrics in regression problems are:
- Mean squared error (MSE)
- Root Mean Squared Error (RMSE)
- Mean absolute error (MAE)
Overall, these metrics are the most frequently used, but there are hundreds of different ones.
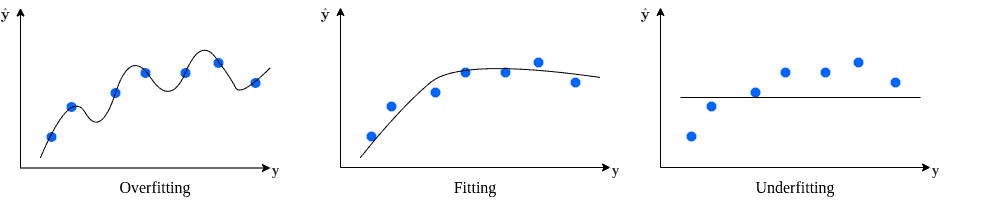
3.2. Underfitting and Overfitting
After choosing the metric, we’re going to set up the validation strategy, also known as cross-validation. One classic way of doing that is to split the whole data set into training and test set. Namely, it’s important to say that selecting the model with the highest accuracy on the training set doesn’t guarantee that it’ll perform similarly in the future with the new data.
Thus, the point of validation is to provide at least the approximate performance of the model for data that will appear in the future. In addition, we need to have in mind the importance of balancing between underfitting and overfitting.
Briefly, the underfitting means that the model doesn’t perform well on both training and test set. Most likely, the reason for underfitting is that model is not well-tuned on the training set or not trained enough. The consequence of that is high bias and low variance.
The overfitting implies that the model is too tuned to the training set. As a result, the model performs very well on the training set but poorly on the test set. The consequence of that is low bias and high variance:
4. K-Fold Cross-Validation
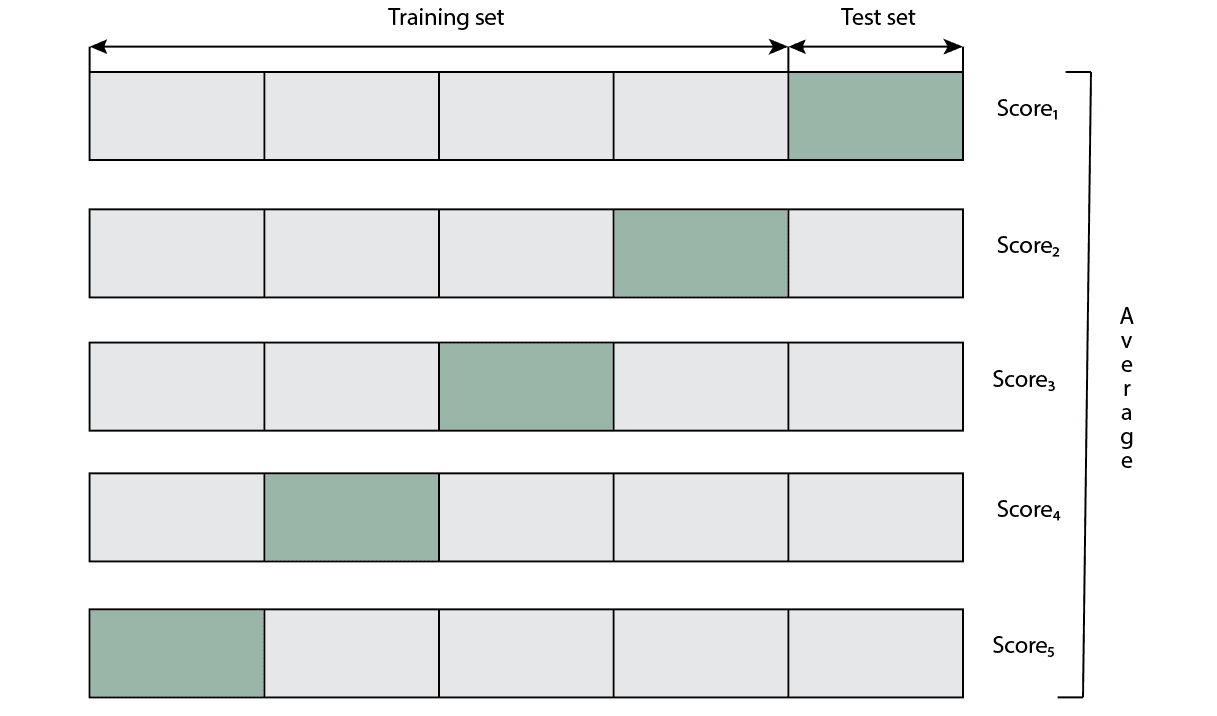
The most significant disadvantage of splitting the data into one training and test set is that the test set might not follow the same distribution of classes in general in the data. Also, some numerical features might not have the same distribution in the training and test set. The k-fold cross validation smartly solves this. Basically, it creates the process where every sample in the data will be included in the test set at some steps.
First, we need to define that represents a number of folds. Usually, it’s in the range of 3 to 10, but we can choose any positive integer. After that, we split the data into
equal folds (parts). The algorithm has
steps where at each step, we select different folds for the test set and the remaining folds we leave for the training set.
Using this method, we will train our model times independently and have
scores measured by some of the selected metrics. Lastly, we can average all scores or even analyze their deviations. We presented the whole process in the image below:
Besides the classic k-fold cross-validation scheme, there are some modifications that we’ll mention below.
4.1. Leave-One-Out Cross-Validation
Leave-one-out cross-validation (LOOCV) is a special type of k-fold cross-validation. There will be only one sample in the test set. Basically, the only difference is that is equal to the number of samples in the data.
Instead of LOOCV, it is preferable to use the leave-p-out strategy, where defines several samples in the training set. Subsequently, the special case of leave-p-out for
is LOOCV. The most significant advantage of this approach is that it uses almost all data in the training set but still requires building
models that can be computationally expensive.
4.2. Stratified K-Fold Cross-Validation
This technique is a type of k-fold cross-validation, intended to solve the problem of imbalanced target classes. For instance, if the goal is to make a model that will predict if the e-mail is spam or not, likely, target classes in the data set won’t be balanced. This is because, in real life, most e-mails are non-spam.
Hence, stratified k-fold cross validation solves this problem by splitting the data set in folds, where each fold has approximately the same distribution of target classes. Similarly, in the case of regression, this approach creates folds that have approximately the same mean target value.
4.3. Repeated K-Fold Cross-Validation
Repeated k-fold cross-validation is a simple strategy that repeats the process of randomly splitting the data set into training and test set times. Unlike classic k-fold cross-validation, this method doesn’t divide data into
folds but randomly splits the data
times. It means that the proportion between training and test set doesn’t depend on the number of folds, but we can set it at any ratio.
Because of that, some samples might be selected multiple times for the test, while some samples might never be selected.
4.4. Nested K-Fold Cross-Validation
Nested k-fold cross-validation is an extension of classic k-fold cross-validation, and it’s mainly used for hyperparameter tuning. It solves two problems that we have in the normal cross-validation:
- Possibility of information leakage.
- The error estimation is made on the exact data for which we found the best hyperparameters, which might be biased.
It’s not best to use the same training and test sets for selecting hyperparameters and estimating error (score). Because of that, we’ll create two k-fold cross-validations, one inside another as nested loops. Through the inner loop, we search hyperparameters while the outer loop is for error estimation. The whole process is illustrated in the image below:
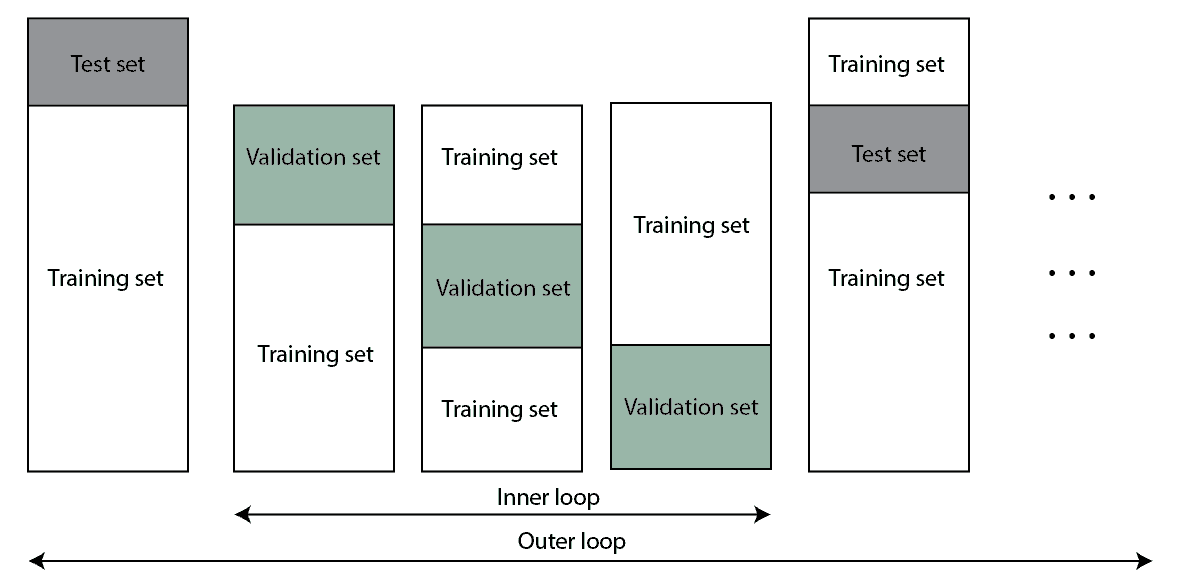
The algorithm for nested k-fold cross-validation is below:
5. Conclusion
In general, validation is an essential step in the machine learning pipeline. That is why we need to pay attention to validation since a small mistake can lead to biased and wrong models. This article explained some of the most common cross-validation techniques that we can use for training neural networks or any other machine learning models.
To conclude, If it’s not computationally too expensive, the suggestion is to use nested k-fold cross-validation. More complex models will most likely work well with classic k-fold cross-validation.