1. Overview
In this tutorial, we’ll discuss two popular approaches to solving computer science and mathematics problems: greedy and heuristic algorithms.
We’ll talk about the basic theoretical idea of both the approaches and present the core differences between them.
2. Theoretic Idea of Greedy Algorithm
Greedy algorithms are mainly used for solving mathematical optimization problems. We either minimize or maximize the cost function corresponding to the given problem in optimization.
There are various types of methods to solve optimization problems. Greedy algorithms are the most used and simplest way to solve optimization problems.
A greedy algorithm divides a given problem into some stages. The main idea is to get an optimal result at each stage using heuristics. We use the solution of each stage as an input for the next stage and find the globally optimal solution.
The heuristics at each stage would be to choose a locally optimal solution that will lead to a globally best fit solution.
A greedy algorithm doesn’t guarantee to produce an optimal solution all the time, but it can give us a globally approximate solution of a given problem in efficient time.
Let’s take a real-life example:
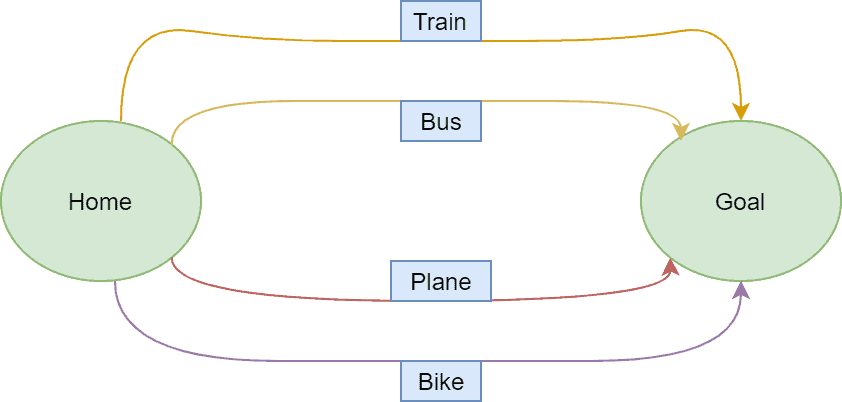
Suppose Jack plans a trip to a hill station and he wants the cheapest (with respect to money) and shortest (in time) way to reach the destination. Hence, he has to choose the best way to reach it. In order to do that, he draws a graph of all possible ways to reach the target destination.
As the diagram shows, there are various ways to reach the destination. Here Jack can use a greedy algorithm. The heuristic strategy of choosing the best path would be calculating the fare per time (per hour) for each route. Based on the result, he can decide the optimal solution as more than one feasible solution.
But we can’t say that the current solution is the best because he just decided on currently available data without considering any further aspects.
It may happen the path he chooses is the cheapest and the shortest, but it’s not compulsory the best path. Perhaps the path picked by him can be dangerous or not in good condition. So the optimality is not guaranteed by a greedy algorithm.
Many programming problems use greedy algorithms. Popular algorithms are the Dijkstra algorithm, Prim’s minimal spanning tree algorithm, Knapsack, and min-max in arrays.
3. Cases of Failure
A greedy algorithm doesn’t guarantee to provide an optimal solution. Sometimes the solution provided by the greedy approach is far from the optimal solution. Let’s discuss an example of coin counting in order to show a situation when the greedy solution is far from the optimal solution.
Let’s assume in our currency system; we have coins worth . Our objective is to count a specific value,
, using the least possible coins. An optimal solution will pick
coins worth
and
coin worth
in order to match desired value. Hence, an optimal algorithm will pick
coins in total.
However, a greedy algorithm will first pick the coin with maximum value from the available coins. So it’ll pick coin worth
and
coins worth
. Hence a greedy algorithm uses
coins in order to count the given value
.
4. Fundamentals of Heuristic Algorithm
It’s used to design the solutions to the problems as quickly as possible. It may not produce the best solution, but it’ll give a near-optimal solution in a short time.
Heuristic algorithms are used to solve NP problems and decrease the time complexity of problems by giving quick solutions. It’s popularly utilized in artificial intelligence problems. One example is informed search, where additional information is available to determine the next step towards finding the solution.
In the heuristic algorithm, a heuristic function gives the heuristic value to find the optimal solution. Each node has a heuristic value that is used to find the optimal path:
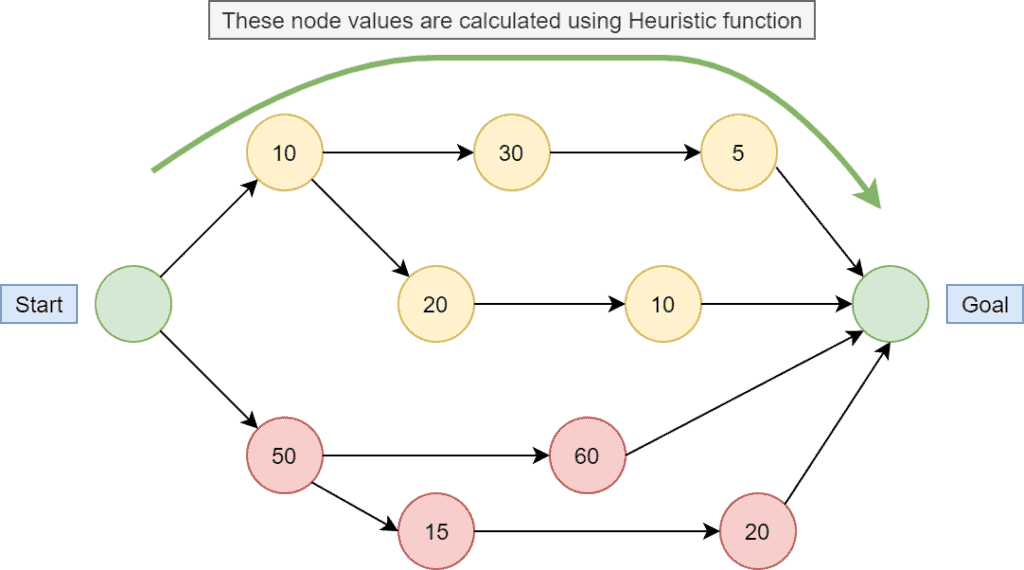
There are two types of heuristic functions: admissible, non-admissible.
In the admissible heuristic function, it never overestimates the cost of reaching the goal. On the other hand, the non-admissible heuristic function overestimates the cost of reaching the goal. Let’s take an example to show the difference between two functions:
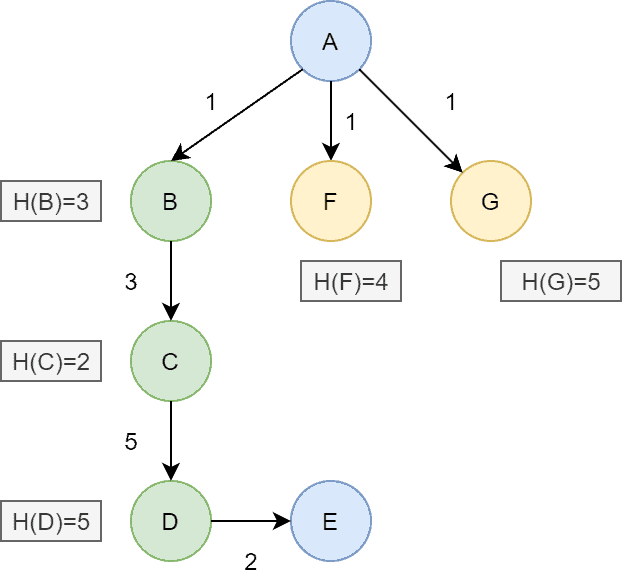
Here the actual cost from to
is
. We’ve calculated the heuristic value of every node using some heuristic function and it’s given in the figure. We can see the heuristic value for node
, for node
, for node
.
The heuristic value is less than the actual cost at each node. It’s an example of an admissible heuristic function. In the case of a non-admissible heuristic function, the heuristic value of each node would be higher than the actual cost.
Several problems use the heuristic method, such as the A* algorithm, Traveling Salesman problem, Simulated Annealing, and the Hill Climbing problem.
5. Trade-Off Conditions
As we already discussed, a heuristic algorithm is not guaranteed to provide an optimal solution, and it’s not advisable to apply the heuristic algorithm to any given problem. The heuristic algorithm might be a good fit for the problems that belong to the NP-Hard class, and there are no known solutions.
There exist some trade-off conditions which give a prior idea of whether a heuristic algorithm is a good fit or not for a given problem. The first condition is the completeness of the problem. If there are several solutions that exist for a given problem, it’s better not to apply a heuristic algorithm. A heuristic algorithm, in general, provides one solution which may not be best among all the available solutions.
Whether to use a heuristic algorithm or not also depends on the optimality of the problem. Suppose if we want to determine to find only the optimal solution, a heuristic may fail to produce so.
When picking a heuristic algorithm, we need to consider the execution time and see if the time taken by the heuristic algorithm is better than the classic algorithm. Suppose it’s marginally faster than the existing methods. In that case, it’s better to choose the existing classic methods as the overhead of the heuristic might increase the time complexity for bigger inputs.
6. Differences Between Greedy and Heuristic Algorithm
Let’s talk about the differences between greedy and heuristic algorithms:
7. Conclusion
In this tutorial, we discussed the general idea of greedy and heuristic algorithms. We also presented a table with the core differences between both approaches.