1. Introduction
In this tutorial, we’ll learn about the Simulated Annealing algorithm and we’ll show the example implementation based on the Traveling Salesman Problem (TSP).
2. Simulated Annealing
The Simulated Annealing algorithm is a heuristic for solving the problems with a large search space.
The Inspiration and the name came from annealing in metallurgy; it is a technique that involves heating and controlled cooling of a material.
In general, the Simulated Annealing decreases the probability of accepting worse solutions as it explores the solution space and lowers the temperature of the system. The following animation shows the mechanism of finding the best solution with the Simulated Annealing algorithm:
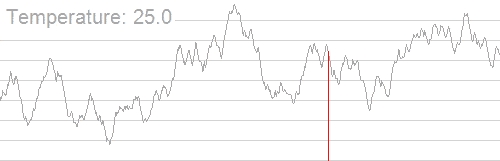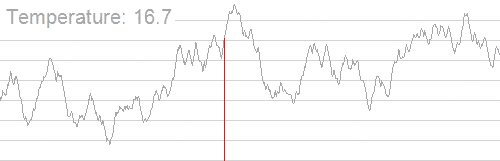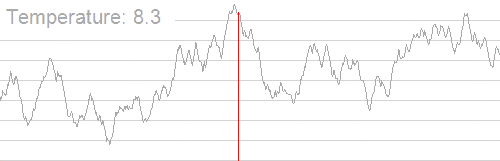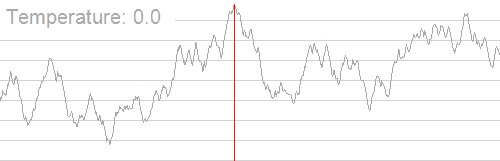
As we may observe, the algorithm uses a wider solution range with high temperature of the system, searching for global optimum. While lowering the temperature, the search range is becoming smaller, until it finds the global optimum.
The algorithm has a few few parameters to work with:
- number of iterations – stopping condition for simulations
- initial temperature – the starting energy of the system
- cooling rate parameter – the percentage by which we reduce the temperature of the system
- minimum temperature – optional stopping condition
- simulation time – optional stopping condition
The values of those parameters must be carefully selected – since they may have significant influence on the performance of the process.
3. Traveling Salesman Problem
The Travelling Salesman Problem (TSP) is the most known computer science optimization problem in a modern world.
In simple words, it is a problem of finding optimal route between nodes in the graph. The total travel distance can be one of the optimization criterion. For more details on TSP please take a look here.
4. Java Model
In order to solve the TSP problem, we’ll need two model classes, namely City and Travel. In the first one, we’ll store the coordinates of the nodes in the graph:
@Data
public class City {
private int x;
private int y;
public City() {
this.x = (int) (Math.random() * 500);
this.y = (int) (Math.random() * 500);
}
public double distanceToCity(City city) {
int x = Math.abs(getX() - city.getX());
int y = Math.abs(getY() - city.getY());
return Math.sqrt(Math.pow(x, 2) + Math.pow(y, 2));
}
}
The constructor of City class allows us to create random locations of the cities. The distanceToCity(..) logic is responsible for calculations regarding the distance between the cities.
The following code is responsible for modeling a traveling salesman tour. Let’s start with generating initial order of cities in travel:
public void generateInitialTravel() {
if (travel.isEmpty()) {
new Travel(10);
}
Collections.shuffle(travel);
}
In addition to generating the initial order, we need the methods for swapping the random two cities in the traveling order. We’ll use it to search for the better solutions inside the Simulated Annealing algorithm:
public void swapCities() {
int a = generateRandomIndex();
int b = generateRandomIndex();
previousTravel = new ArrayList<>(travel);
City x = travel.get(a);
City y = travel.get(b);
travel.set(a, y);
travel.set(b, x);
}
Furthermore, we need a method to revert the swap generating in the previous step, if the new solution will be not accepted by our algorithm:
public void revertSwap() {
travel = previousTravel;
}
The last method that we want to cover is the calculation of the total travel distance, which will be used as an optimization criterion:
public int getDistance() {
int distance = 0;
for (int index = 0; index < travel.size(); index++) {
City starting = getCity(index);
City destination;
if (index + 1 < travel.size()) {
destination = getCity(index + 1);
} else {
destination = getCity(0);
}
distance += starting.distanceToCity(destination);
}
return distance;
}
Now, let’s focus on the main part, the Simulated Annealing algorithm implementation.
5. Simulated Annealing Implementation
In the following Simulated Annealing implementation, we are going to solve the TSP problem. Just a quick reminder, the objective is to find the shortest distance to travel all cities.
In order to start process, we need to provide three main parameters, namely startingTemperature, numberOfIterations and coolingRate:
public double simulateAnnealing(double startingTemperature,
int numberOfIterations, double coolingRate) {
double t = startingTemperature;
travel.generateInitialTravel();
double bestDistance = travel.getDistance();
Travel currentSolution = travel;
// ...
}
Before the start of the simulation, we generate initial (random) order of cities and calculate the total distance for travel. As this is the first calculated distance, we save it inside the bestDistance variable, alongside with the currentSolution.
In the next step we start a main simulations loop:
for (int i = 0; i < numberOfIterations; i++) {
if (t > 0.1) {
//...
} else {
continue;
}
}
The loop will last the number of iterations that we specified. Moreover, we added a condition to stop the simulation if the temperature will be lower or equal to 0.1. It will allow us to save the time of simulations, as with low temperatures the optimization differences are almost not visible.
Let’s look at the main logic of the Simulated Annealing algorithm:
currentSolution.swapCities();
double currentDistance = currentSolution.getDistance();
if (currentDistance < bestDistance) {
bestDistance = currentDistance;
} else if (Math.exp((bestDistance - currentDistance) / t) < Math.random()) {
currentSolution.revertSwap();
}
In each step of simulation we randomly swap two cities in the traveling order.
Furthermore, we calculate the currentDistance. If the newly calculated currentDistance is lower than bestDistance, we save it as the best.
Otherwise, we check if Boltzmann function of probability distribution is lower than randomly picked value in a range from 0-1. If yes, we revert the swap of the cities. If not, we keep the new order of the cities, as it can help us to avoid the local minima.
Finally, in each step of the simulation we reduce the temperature by provided coolingRate:
t *= coolingRate;
After the simulation we return the best solution that we found using Simulated Annealing.
Please note the few tips on how to choose the best simulation parameters:
- for small solution spaces it’s better to lower the starting temperature and increase the cooling rate, as it will reduce the simulation time, without lose of quality
- for bigger solution spaces please choose the higher starting temperature and small cooling rate, as there will be more local minima
- always provide enough time to simulate from the high to low temperature of the system
Don’t forget to spend some time on the algorithm tuning with the smaller problem instance, before you start the main simulations, as it will improve final results. The tuning of the Simulated Annealing algorithm was shown for example in this article.
6. Conclusion
In this quick tutorial we were able to learn about the Simulated Annealing algorithm and we solved the Travelling Salesman Problem. This hopefully goes to show how handy is this simple algorithm, when applied to certain types of optimization problems.
The full implementation of this article can be found over on GitHub.






