Example of Hill Climbing Algorithm in Java

1. Overview

In this tutorial, we’ll show the Hill-Climbing algorithm and its implementation. We’ll also look at its benefits and shortcomings. Before directly jumping into it, let’s discuss generate-and-test algorithms approach briefly.

2. Generate-And-Test Algorithm

It’s a very simple technique that allows us to algorithmize finding solutions:

1. Define current state as an initial state
2. Apply any possible operation on the current state and generate a possible solution
3. Compare newly generated solution with the goal state
4. If the goal is achieved or no new states can be created, quit. Otherwise, return to the step 2

It works very well with simple problems. As it is an exhaustive search, it is not feasible to consider it while dealing with large problem spaces. It is also known as British Museum algorithm (trying to find an artifact in the British Museum by exploring it randomly).

It is also the main idea behind the Hill-Climbing Attack in the world of biometrics. This approach can be used for generating synthetic biometric data.

3. Introduction to the Simple Hill-Climbing Algorithm

In Hill-Climbing technique, starting at the base of a hill, we walk upwards until we reach the top of the hill. In other words, we start with initial state and we keep improving the solution until its optimal.

It’s a variation of a generate-and-test algorithm which discards all states which do not look promising or seem unlikely to lead us to the goal state. To take such decisions, it uses heuristics (an evaluation function) which indicates how close the current state is to the goal state.

In simple words, Hill-Climbing = generate-and-test + heuristics

Let’s look at the Simple Hill climbing algorithm:

1. Define the current state as an initial state
2. Loop until the goal state is achieved or no more operators can be applied on the current state:
   1. Apply an operation to current state and get a new state
   2. Compare the new state with the goal
   3. Quit if the goal state is achieved
   4. Evaluate new state with heuristic function and compare it with the current state
   5. If the newer state is closer to the goal compared to current state, update the current state

As we can see, it reaches the goal state with iterative improvements. In Hill-Climbing algorithm, finding goal is equivalent to reaching the top of the hill.

4. Example

Hill Climbing Algorithm can be categorized as an informed search. So we can implement any node-based search or problems like the n-queens problem using it. To understand the concept easily, we will take up a very simple example.

Let’s look at the image below:

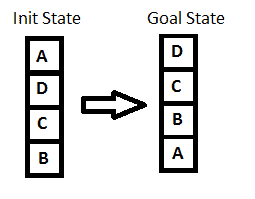
Key point while solving any hill-climbing problem is to choose an appropriate heuristic function.

Let’s define such function h:

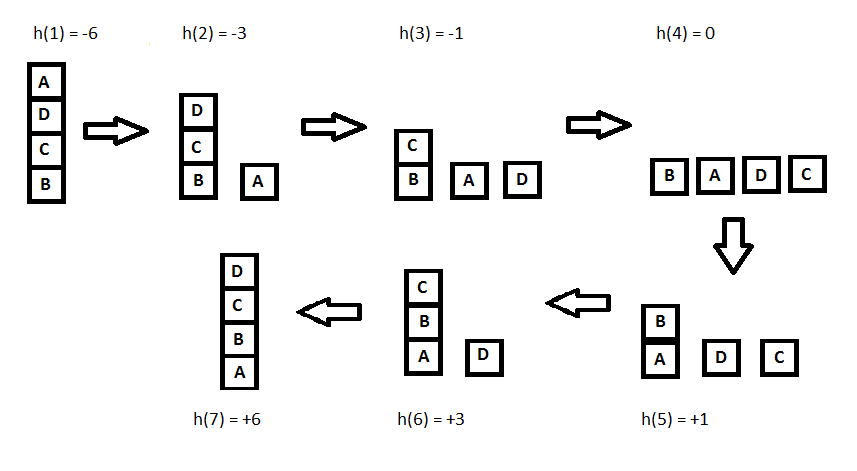
h(x) = +1 for all the blocks in the support structure if the block is correctly positioned otherwise -1 for all the blocks in the support structure.

Here, we will call any block correctly positioned if it has the same support structure as the goal state. As per the hill climbing procedure discussed earlier let’s look at all the iterations and their heuristics to reach the target state:

5. Implementation

Now, let’s implement the same example using the Hill-Climbing algorithm.

First of all, we need a State class which will store the list of stacks representing positions of blocks at each state. It will also store heuristics for that particular state:

public class State {
    private List<Stack<String>> state;
    private int heuristics;
    
    // copy constructor, setters, and getters
}

We also need a method which will compute the heuristic value of the state.

public int getHeuristicsValue(
  List<Stack<String>> currentState, Stack<String> goalStateStack) {
 
    Integer heuristicValue;
    heuristicValue = currentState.stream()
      .mapToInt(stack -> {
          return getHeuristicsValueForStack(
            stack, currentState, goalStateStack);
    }).sum();
 
    return heuristicValue;
}

public int getHeuristicsValueForStack(
  Stack<String> stack,
  List<Stack<String>> currentState,
  Stack<String> goalStateStack) {

    int stackHeuristics = 0;
    boolean isPositioneCorrect = true;
    int goalStartIndex = 0;
    for (String currentBlock : stack) {
        if (isPositioneCorrect 
          && currentBlock.equals(goalStateStack.get(goalStartIndex))) {
            stackHeuristics += goalStartIndex;
        } else {
            stackHeuristics -= goalStartIndex;
            isPositioneCorrect = false;
        }
        goalStartIndex++;
    }
    return stackHeuristics;
}

Furthermore, we need to define operator methods which will get us a new state. For our example we will define two of these methods:

1. Pop a block from a stack and push it onto a new stack
2. Pop a block from a stack and push it into one of the other stacks

private State pushElementToNewStack(
  List<Stack<String>> currentStackList,
  String block,
  int currentStateHeuristics,
  Stack<String> goalStateStack) {
 
    State newState = null;
    Stack<String> newStack = new Stack<>();
    newStack.push(block);
    currentStackList.add(newStack);
    int newStateHeuristics 
      = getHeuristicsValue(currentStackList, goalStateStack);
    if (newStateHeuristics > currentStateHeuristics) {
        newState = new State(currentStackList, newStateHeuristics);
    } else {
        currentStackList.remove(newStack);
    }
    return newState;
}

private State pushElementToExistingStacks(
  Stack currentStack,
  List<Stack<String>> currentStackList,
  String block,
  int currentStateHeuristics,
  Stack<String> goalStateStack) {

    return currentStackList.stream()
      .filter(stack -> stack != currentStack)
      .map(stack -> {
          return pushElementToStack(
            stack, block, currentStackList,
            currentStateHeuristics, goalStateStack);
        })
      .filter(Objects::nonNull)
      .findFirst()
      .orElse(null);
}

private State pushElementToStack(
  Stack stack,
  String block,
  List<Stack<String>> currentStackList,
  int currentStateHeuristics,
  Stack<String> goalStateStack) {

    stack.push(block);
    int newStateHeuristics 
      = getHeuristicsValue(currentStackList, goalStateStack);
    if (newStateHeuristics > currentStateHeuristics) {
        return new State(currentStackList, newStateHeuristics);
    }
    stack.pop();
    return null;
}

Now that we have our helper methods let’s write a method to implement hill climbing technique.

Here, we keep computing new states which are closer to goals than their predecessors. We keep adding them in our path until we reach the goal.

If we don’t find any new states, the algorithm terminates with an error message:

public List<State> getRouteWithHillClimbing(
  Stack<String> initStateStack, Stack<String> goalStateStack) throws Exception {
    // instantiate initState with initStateStack
    // ...
    List<State> resultPath = new ArrayList<>();
    resultPath.add(new State(initState));

    State currentState = initState;
    boolean noStateFound = false;
    
    while (
      !currentState.getState().get(0).equals(goalStateStack)
      || noStateFound) {
        noStateFound = true;
        State nextState = findNextState(currentState, goalStateStack);
        if (nextState != null) {
            noStateFound = false;
            currentState = nextState;
            resultPath.add(new State(nextState));
        }
    }
    return resultPath;
}

In addition to this, we also need findNextState method which applies all possible operations on current state to get the next state:

public State findNextState(State currentState, Stack<String> goalStateStack) {
    List<Stack<String>> listOfStacks = currentState.getState();
    int currentStateHeuristics = currentState.getHeuristics();

     return listOfStacks.stream()
      .map(stack -> {
          return applyOperationsOnState(
            listOfStacks, stack, currentStateHeuristics, goalStateStack);
      })
      .filter(Objects::nonNull)
      .findFirst()
      .orElse(null);
}

public State applyOperationsOnState(
  List<Stack<String>> listOfStacks,
  Stack<String> stack,
  int currentStateHeuristics,
  Stack<String> goalStateStack) {

    State tempState;
    List<Stack<String>> tempStackList 
      = new ArrayList<>(listOfStacks);
    String block = stack.pop();
    if (stack.size() == 0)
      tempStackList.remove(stack);
    tempState = pushElementToNewStack(
      tempStackList, block, currentStateHeuristics, goalStateStack);
    if (tempState == null) {
        tempState = pushElementToExistingStacks(
          stack, tempStackList, block,
          currentStateHeuristics, goalStateStack);
        stack.push(block);
    }
    return tempState;
}

6. Steepest-Ascent Hill Climbing Algorithm

Steepest-Ascent Hill-Climbing algorithm (gradient search) is a variant of Hill Climbing algorithm. We can implement it with slight modifications in our simple algorithm. In this algorithm, we consider all possible states from the current state and then pick the best one as successor, unlike in the simple hill climbing technique.

In other words, in the case of hill climbing technique we picked any state as a successor which was closer to the goal than the current state whereas, in Steepest-Ascent Hill Climbing algorithm, we choose the best successor among all possible successors and then update the current state.

7. Disadvantages

Hill Climbing is a short sighted technique as it evaluates only immediate possibilities. So it may end up in few situations from which it can not pick any further states. Let’s look at these states and some solutions for them:

1. Local maximum: It’s a state which is better than all neighbors, but there exists a better state which is far from the current state; if local maximum occurs within sight of the solution, it is known as “foothills”
2. Plateau: In this state, all neighboring states have same heuristic values, so it’s unclear to choose the next state by making local comparisons
3. Ridge: It’s an area which is higher than surrounding states, but it can not be reached in a single move; for example, we have four possible directions to explore (N, E, W, S) and an area exists in NE direction

There are few solutions to overcome these situations:

1. We can backtrack to one of the previous states and explore other directions
2. We can skip few states and make a jump in new directions
3. We can explore several directions to figure out the correct path

8. Conclusion

Even though hill climbing technique is much better than exhaustive search, it’s still not optimal in large problem spaces.

We can always encode global information into heuristic functions to make smarter decisions, but then computational complexity will be much higher than it was earlier.

Hill climbing algorithm can be very beneficial when clubbed with other techniques. As always, the complete code for all examples can be found over on GitHub.