Vertex Coloring in Graphs | Baeldung on Computer Science

1. Introduction

In this tutorial, we’ll explore vertex coloring in graphs.

2. Vertex Coloring

A graph $G=(V, E)$ is a collection of nodes (vertices) $V$ and edges $E$ such that every edge $e \in E$ joins two vertices from $V$ . For example:

We look at the problem of coloring all nodes of a loopless graph with unique colors. To clarify, a loopless graph is one in which no node has an edge connecting it to itself.

Vertex (or node) coloring of $\boldsymbol{G}$ means finding an assignment $\boldymbol{f}$ that colors each vertex so that no two neighboring vertices have the same color. For instance:

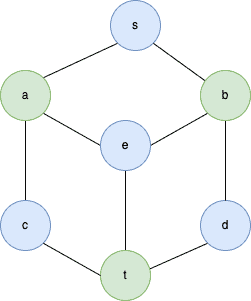
Formally, a proper vertex coloring $f$ of $G$ is a mapping $f: V \rightarrow \{1, 2, 3, \ldots, K\}$ , where $1, 2, \ldots, K$ are colors, such that no two adjacent vertices have the same color:

$(\forall u, v \in V) ((\exists e \in E)(e\text{ joins }u\text{ and }v)) \implies f(u) \neq f(v)$

If there’s a proper coloring of a graph $G$ with $K$ colors, we say that $G$ is $K$ -colorable.

3. Chromatic Number

We define the chromatic number of $G$ (denoted by $\chi(G)$ ) as the minimum number of colors required to vertex color $G$ . In other words, it’s the smallest $\boldsymbol{K}$ such that $\boldsymbol{G}$ is $\boldsymbol{K}$ -colorable.

3.1. Properties

First, for a graph $G=(V, E)$ where $|V|=N$ , it holds that $\chi(G) \leq N$ . Second, for a complete graph $G$ , $\chi(G) = N$ since each vertex is connected to the remaining $N-1$ vertices. On similar lines, $\chi(G)=1$ where $G$ is a null graph.

Moving on, if $H$ is a sub-graph of $G$ , then $\chi(G) \geq \chi(H)$ . This is intuitive since $H$ would need no more colors than $G$ because $H$ has no more nodes than $G$ .

3.2. NP-Completeness

Determining the chromatic number for a generic graph is an NP-complete problem.

These problems are of great interest to computer scientists because they arise in many practical applications, but no algorithm with the worst-case polynomial complexity is known to solve them.

3.3. Color Classes

The nodes of a $K$ -colorable graph $G$ can be partitioned into $K$ independent sets: $V_{1}, V_{2}, \ldots, V_{K}$ . Here, no two vertices in a set are adjacent to each other.

For our vertex-coloring example graph $G(V,E)$ , we have $\chi(G)=2$ , so $V_{Blue}=\{s, e, c, d\}$ and $V_{Green}=\{a, b, t\}$ . Both $V_{Blue}$ and $V_{Green}$ are independent as $V_{Blue} \cap V_{Green} = \var$ and $V_{Blue} \cup V_{Green} = V$ .

4. Algorithm

In this section, we present a greedy algorithm for determining the chromatic number of a graph. It isn’t an exact algorithm, which means it returns an upper bound on $\chi$ :

4.2. Explanation

We start with the given graph $G(V, E)$ with $|V|=N$ .

Firstly, we set the colors of all the nodes -1 to denote that all vertices at the start are uncolored (white).

Then, we iterate over the nodes sorted by their degrees. There are $N$ options for each node in the beginning ( $AvailableColors$ ). We disregard the colors assigned to its neighbors and give it the minimal color code remaining in $AvailableColors$ .

After processing all the nodes, the algorithm returns the maximum color code as the chromatic number. Since this is a greedy algorithm, the returned number is only an estimate and should be treated as the upper bound of $\chi(G)$ .

4.3. Space and Time Complexity

The time complexity of this algorithm depends on how we implement $AvailableColors$ and $Colors$ . If we use hash tables, the overall time complexity will be $O(N^{2})$ .

The space complexity is also $O(N ^{2})$ because of the upper bound on the number of edges in a graph with $N$ nodes.

4.4. Example

Let’s check out an example:

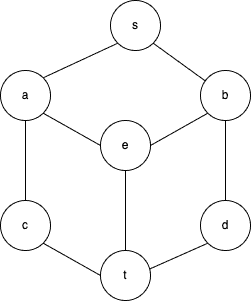
Initially, all the nodes are white ( $(\forall v \in V) Colors[v] = -1$ ). Since there are seven nodes, each vertex in the main loop will start with seven available colors. Let their codes be $\{$ blue=1, green=2, red=3, pink=4, black=5, brown=6, violet=7 $\}$ .

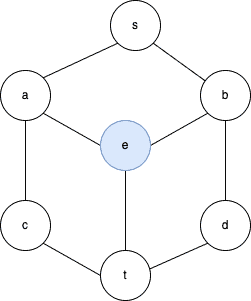
We start with vertex $e$ , which has the highest degree (3). Its neighbors are $\{a, b, t\}$ . All are white, so we color $e$ as blue since that’s the minimum of $\{1,2,3,4,5,6,7\}$ :

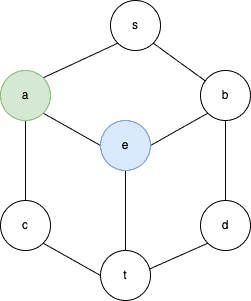
Next, we take vertex $a$ . Its neighbors are $\{ s, e, c\}$ . Since $e$ is blue, we disregard the color 1 and assign $a$ the minimum of the remaining codes (2):

Now comes the turn of $b$ . Its neighbors are $\{ s, e, d\}$ . The reasoning is the same as for $a$ , so we color it green:

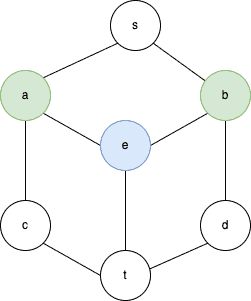
Continuing like this, we color this graph using two colors (blue and green), which gives us $\chi(G)=2$ .

5. Applications

This enables us to run various operations on graphs to solve specific problems.

5.1. Exam Scheduling

Here, we consider the problem of scheduling exams in a university. Typically, we have different subjects and will have many students enrolled in each subject. Further, each student can be enrolled in more than one subject, and each subject will have more than one enrolled student.

We need to schedule exams such that no two exams with at least one common student are on the same day. Additionally, we want to schedule all exams in the minimal possible number of days. How do we solve this? Vertex coloring comes to our rescue:

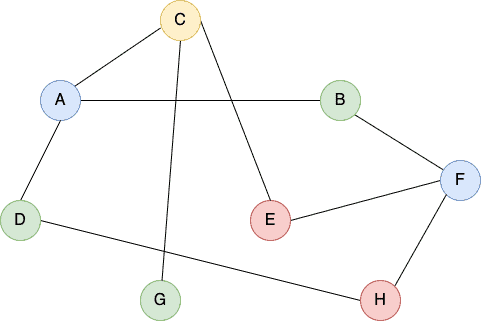
We represent this problem as a graph where we model each subject as a vertex. We introduce an edge between two vertices if the corresponding subjects have at least one student in common. Then, we find the graph’s chromatic number. It’s equal to the minimum number of days necessary to schedule all the exams simultaneously without a clash.

In our example, we’ll have 8 exams over 4 days.

5.2. Radio Frequency Assignment

Another application comes from the frequency assignment to radio towers. Here, we have several towers and need to use the smallest number of frequencies for communication.

Again, we model this as a graph coloring problem where we set each tower as a vertex. Then, we construct an edge between two towers if they are in interfering range with each other. After that, we apply vertex coloring and get our chromatic number, which shows us the minimal number of frequencies we need.

6. Conclusion

In this article, we studied vertex coloring in graphs and finding the chromatic number. An excellent way to understand this problem is to consider it an optimization problem. Given a graph $G$ , we minimize the number of colors needed to color it so that no two neighbors have the same color.

This problem has diverse applications, including clustering, data mining, digital image processing, computer networks, resource allocation, unconstraint optimization, and process scheduling.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex