1. Overview
In this tutorial, we’ll look at how to implement a min-max heap in Java.
2. Min-Max Heap
First of all, let’s look at heap’s definition and characteristics. The min-max heap is a complete binary tree with both traits of min heap and max heap:
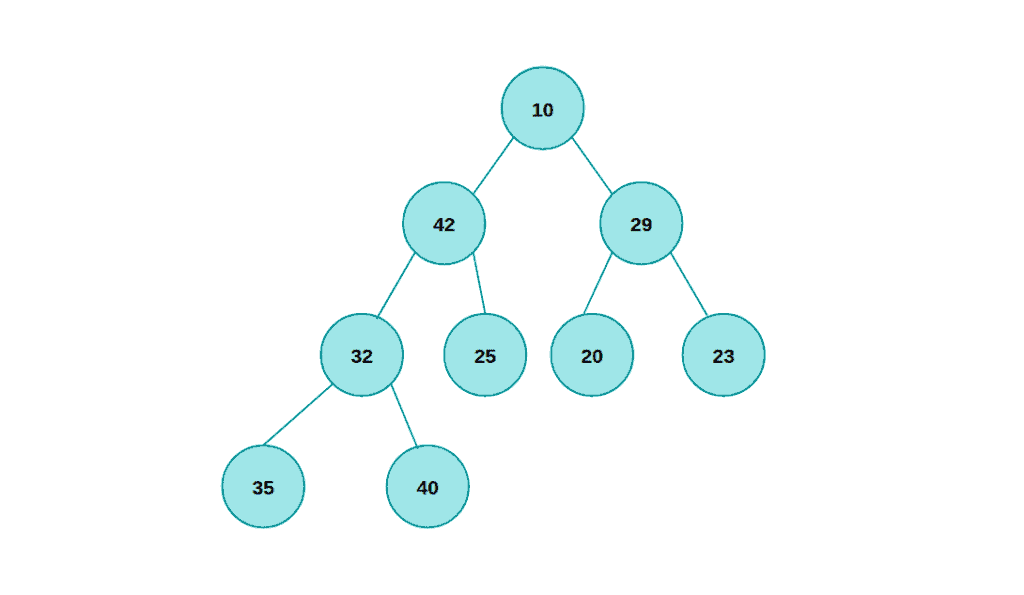
As we can see above, each node at an even level in the tree is less than all of its descendants, while each node at an odd level in the tree is greater than all of its descendants, where the root is at level zero.
Each node in the min-max heap has a data member that is usually called a key. The root has the smallest key in the min-max heap, and one of the two nodes in the second level is the greatest key. For each node like X in a min-max heap:
- If X is on a min (or even) level, then X.key is the minimum key among all keys in the subtree with root X
- If X is on a max (or odd) level, then X.key is the maximum key among all keys in the subtree with root X
Like min-heap or max-heap, insertion and deletion can occur in the time complexity of O(logN).
3. Implementation in Java
Let’s start with a simple class that represents our min-max heap:
public class MinMaxHeap<T extends Comparable<T>> {
private List<T> array;
private int capacity;
private int indicator;
}
As we can see above, we use an indicator to figure out the last item index added to the array. But before we continue, we need to remember that the array index starts from zero, but we assume the index starts from one in a heap.
We can find the index of left and right children using the following methods:
private int getLeftChildIndex(int i) {
return 2 * i;
}
private int getRightChildIndex(int i) {
return ((2 * i) + 1);
}
Likewise, we can find the index of parent and grandparent of the item in the array by the following code:
private int getParentIndex(int i) {
return i / 2;
}
private int getGrandparentIndex(int i) {
return i / 4;
}
Now, let’s continue with complete our simple min-max heap class:
public class MinMaxHeap<T extends Comparable<T>> {
private List<T> array;
private int capacity;
private int indicator;
MinMaxHeap(int capacity) {
array = new ArrayList<>();
this.capacity = capacity;
indicator = 1;
}
MinMaxHeap(List<T> array) {
this.array = array;
this.capacity = array.size();
this.indicator = array.size() + 1;
}
}
We can create an instance of the min-max heap in two ways here. First, we initiate an array with an ArrayList and specific capacity, and second, we make a min-max heap from the existing array.
Now, let’s discuss operations on our heap.
3.1. Create
Let’s first look at building a min-max heap from an existing array. Here we use Floyd’s algorithm with some adaption like the Heapify algorithm:
public List<T> create() {
for (int i = Math.floorDiv(array.size(), 2); i >= 1; i--) {
pushDown(array, i);
}
return array;
}
Let’s see what exactly happened in the above code by take a look closer to pushDown in the following code:
private void pushDown(List<T> array, int i) {
if (isEvenLevel(i)) {
pushDownMin(array, i);
} else {
pushDownMax(array, i);
}
}
As we can see, for all even levels, we check array items with pushDownMin. This algorithm is like heapify-down that we’ll use for removeMin and removeMax:
private void pushDownMin(List<T> h, int i) {
while (getLeftChildIndex(i) < indicator) {
int indexOfSmallest = getIndexOfSmallestChildOrGrandChild(h, i);
//...
i = indexOfSmallest;
}
}
First, we find the index of the smallest child or grandchild of the ‘i’ element. Then we proceed according to the following conditions.
If the smallest child or grandchild is not less than the current element, we break. In other words, the current arranges of elements are like min-heap:
if (h.get(indexOfSmallest - 1).compareTo(h.get(i - 1)) < 0) {
//...
} else {
break;
}
If the smallest child or grandchild is smaller than the current element, we swap it with its parent or grandparent:
if (getParentIndex(getParentIndex(indexOfSmallest)) == i) {
if (h.get(indexOfSmallest - 1).compareTo(h.get(i - 1)) < 0) {
swap(indexOfSmallest - 1, i - 1, h);
if (h.get(indexOfSmallest - 1)
.compareTo(h.get(getParentIndex(indexOfSmallest) - 1)) > 0) {
swap(indexOfSmallest - 1, getParentIndex(indexOfSmallest) - 1, h);
}
}
} else if (h.get(indexOfSmallest - 1).compareTo(h.get(i - 1)) < 0) {
swap(indexOfSmallest - 1, i - 1, h);
}
We’ll continue the above operations until found a child for the element ‘i’.
Now, Let’s see how getIndexOfSmallestChildOrGrandChild works. It’s pretty easy! First, we assume the left child has the smallest value then compare it with others:
private int getIndexOfSmallestChildOrGrandChild(List<T> h, int i) {
int minIndex = getLeftChildIndex(i);
T minValue = h.get(minIndex - 1);
// rest of the implementation
}
In each step, if the index is greater than the indicator, the last minimum value found is the answer.
For example, let’s compare min-value with the right child:
if (getRightChildIndex(i) < indicator) {
if (h.get(getRightChildIndex(i) - 1).compareTo(minValue) < 0) {
minValue = h.get(getRightChildIndex(i));
minIndex = getRightChildIndex(i);
}
} else {
return minIndex;
}
Now, let’s create a test to verify that make a min-max heap from an unordered array works fine:
@Test
public void givenUnOrderedArray_WhenCreateMinMaxHeap_ThenIsEqualWithMinMaxHeapOrdered() {
List<Integer> list = Arrays.asList(34, 12, 28, 9, 30, 19, 1, 40);
MinMaxHeap<Integer> minMaxHeap = new MinMaxHeap<>(list);
minMaxHeap.create();
Assert.assertEquals(List.of(1, 40, 34, 9, 30, 19, 28, 12), list);
}
The algorithm for pushDownMax is identical to that for pushDownMin, but with all of the comparison, operators reversed.
3.2. Insert
Let’s see how to add an element to a min-max Heap:
public void insert(T item) {
if (isEmpty()) {
array.add(item);
indicator++;
} else if (!isFull()) {
array.add(item);
pushUp(array, indicator);
indicator++;
} else {
throw new RuntimeException("invalid operation !!!");
}
}
First, we check the heap is empty or not. If the heap is empty, we append the new element and increase the indicator. Otherwise, the new element that added may change the order of the min-max heap, So we need to adjust the heap with pushUp:
private void pushUp(List<T>h,int i) {
if (i != 1) {
if (isEvenLevel(i)) {
if (h.get(i - 1).compareTo(h.get(getParentIndex(i) - 1)) < 0) {
pushUpMin(h, i);
} else {
swap(i - 1, getParentIndex(i) - 1, h);
i = getParentIndex(i);
pushUpMax(h, i);
}
} else if (h.get(i - 1).compareTo(h.get(getParentIndex(i) - 1)) > 0) {
pushUpMax(h, i);
} else {
swap(i - 1, getParentIndex(i) - 1, h);
i = getParentIndex(i);
pushUpMin(h, i);
}
}
}
As we can see above, the new element compares its parent, then:
- If it’s found to be less (greater) than the parent, then it’s definitely less (greater) than all other elements on max (min) levels that are on the path to the root of the heap
- The path from the new element to the root (considering only min/max levels) should be in a descending (ascending) order as it was before the insertion. So, we need to make a binary insertion of the new element into this sequence
Now, Let’s take a look at the pushUpMin as is following:
private void pushUpMin(List<T> h , int i) {
while(hasGrandparent(i) && h.get(i - 1)
.compareTo(h.get(getGrandparentIndex(i) - 1)) < 0) {
swap(i - 1, getGrandparentIndex(i) - 1, h);
i = getGrandparentIndex(i);
}
}
Technically, it’s simpler to swap the new element with its parent while the parent is greater. Also, pushUpMax identical to pushUpMin, but with all of the comparison, operators reversed.
Now, Let’s create a test to verify that insert a new element into a min-max Heap works fine:
@Test
public void givenNewElement_WhenInserted_ThenIsEqualWithMinMaxHeapOrdered() {
MinMaxHeap<Integer> minMaxHeap = new MinMaxHeap(8);
minMaxHeap.insert(34);
minMaxHeap.insert(12);
minMaxHeap.insert(28);
minMaxHeap.insert(9);
minMaxHeap.insert(30);
minMaxHeap.insert(19);
minMaxHeap.insert(1);
minMaxHeap.insert(40);
Assert.assertEquals(List.of(1, 40, 28, 12, 30, 19, 9, 34),
minMaxHeap.getMinMaxHeap());
}
3.3. Find Min
The main element in a min-max heap is always located at the root, so we can find it in time complexity O(1):
public T min() {
if (!isEmpty()) {
return array.get(0);
}
return null;
}
3.4. Find Max
The max element in a min-max heap it’s always located first odd level, so we can find it in time complexity O(1) with a simple comparison:
public T max() {
if (!isEmpty()) {
if (indicator == 2) {
return array.get(0);
}
if (indicator == 3) {
return array.get(1);
}
return array.get(1).compareTo(array.get(2)) < 0 ? array.get(2) : array.get(1);
}
return null;
}
3.5. Remove Min
In this case, we’ll find the min element, then replace it with the last element of the array:
public T removeMin() {
T min = min();
if (min != null) {
if (indicator == 2) {
array.remove(indicator--);
return min;
}
array.set(0, array.get(--indicator - 1));
array.remove(indicator - 1);
pushDown(array, 1);
}
return min;
}
3.6. Remove Max
Removing the max element is the same as remove min, with the only change that we find the index of the max element then call pushDown:
public T removeMax() {
T max = max();
if (max != null) {
int maxIndex;
if (indicator == 2) {
maxIndex = 0;
array.remove(--indicator - 1);
return max;
} else if (indicator == 3) {
maxIndex = 1;
array.remove(--indicator - 1);
return max;
} else {
maxIndex = array.get(1).compareTo(array.get(2)) < 0 ? 2 : 1;
}
array.set(maxIndex, array.get(--indicator - 1));
array.remove(indicator - 1);
pushDown(array, maxIndex + 1);
}
return max;
}
4. Conclusion
In this tutorial, we’ve seen implementing a min-max heap in Java and exploring some of the most common operations.
First, we learned what exactly a min-max heap is, including some of the most common features. Then, we saw how to create, insert, find-min, find-max, remove-min, and remove-max items in our min-max heap implementation.
As usual, all the examples used in this article are available over on GitHub.






