1. Overview
In this tutorial, we’ll go through the main concepts of Heap and Binary Search Tree (BST) data structures. Also, we’ll show their similarities and differences. Moreover, we’ll speak about their internal implementation and time complexity of operations on these data structures. To do it, we’ll use a Big-O notation. We assume having a basic knowledge of Binary Search Tree and Heap data structures.
2. Binary Search Tree
Binary Search Tree is usually represented as an acyclic graph. The tree consists of nodes. In case the tree is binary, each node has at most two children. The BST has an important property: every node’s value is strictly greater than the value of its left child and strictly lower than the value of its right child. It means, we can iterate all the values of the BST in sorted order. Also, this data structure doesn’t allow duplicate values.
Let’s look at the example of the binary trees:
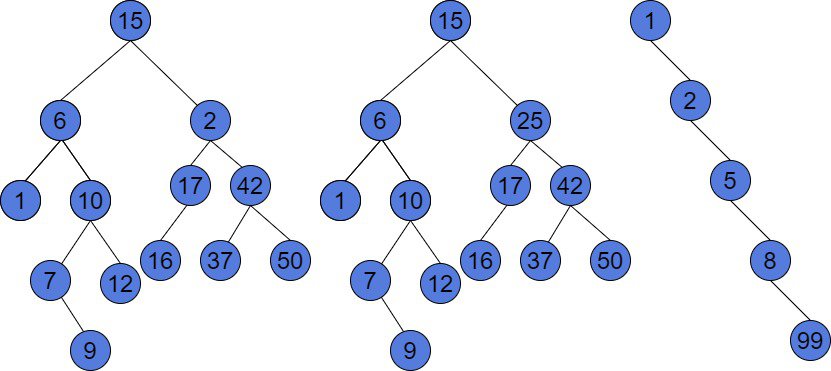
The tree to the left is a binary tree because each node has 0, 1, or 2 children. But, this is not a BST. For instance, the root’s right child is 2. 2 is less than the value of the root, which is 15. Furthermore, for a node with a value of 2, its left child has a value of 17, which also violates the BST property. The other two trees on the above image are the Binary Search Trees because every node satisfies the rules of a BST.
Binary Search Tree can be either balanced and unbalanced. We may notice, that the last tree forms a chain and is unbalanced. But, this is still a Binary Search Tree. None of the rules are violated. However, the insert and remove operations are inefficient in such a tree.
Suppose to be the number of nodes in a BST. The worst case of the insert and remove operations is
. But, in a balanced Binary Search Tree, for instance, in AVL or Red-Black Tree, the time complexity of such operations is
. The other major fact is that building BST of
nodes takes
time. We have to insert a node
times, and each insertion costs
. The big advantage of a Binary Search Tree is that we can get traverse the tree and get all our values in sorted order in
time.
3. Heap
The Heap is a Complete Binary Tree. Let’s introduce some definitions to understand what the Complete Binary Tree is.
A node is at level of the tree if the distance between this node and the root node is
. The level of the root is 0. The maximum possible number of nodes at level k is
. At each level of a Complete Binary Tree, it contains the maximum number of nodes. But, except possibly the last layer, which also must be filled from left to right. Is important to understand, that the Complete Binary Tree is always balanced.
The Heap differs from a Binary Search Tree. The BST is an ordered data structure, however, the Heap is not. In computer memory, the heap is usually represented as an array of numbers. The heap can be either Min-Heap or Max-Heap. The properties of Min- and Max-Heap are almost the same, but the root of the tree is the largest number for the Max-Heap and the smallest for the Min-Heap. Similarly, the main rule of the Max-Heap is that the subtree under each node contains values less or equal than its root node. Whereas, it’s vice versa for the Min-Heap. Also, it means, that the Heap allows duplicates.
In case the Heap is a Complete Binary Tree, it has the minimum possible height for the tree, which is . In an array, where the heap nodes are stored, the children of a node at index
are nodes at indices
and
. It means, that the heap is filled from top to bottom. And at each layer, it is filled from left to right. Let’s look at an example of heaps:
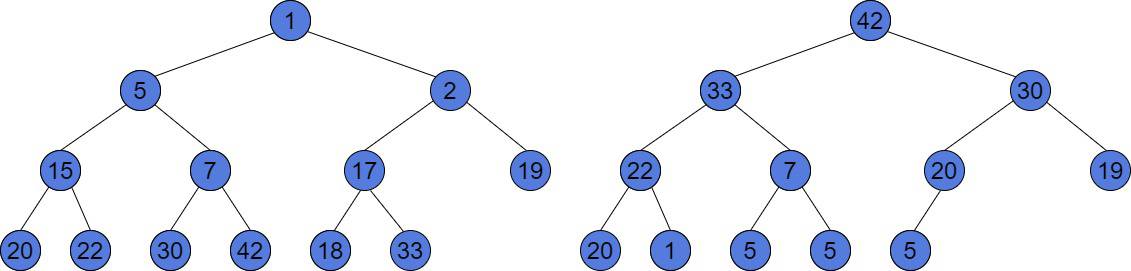
The Heap to the left is a Min-Heap. The smallest value has the root of the tree. And, for every node, all the values under it are greater than the node. The tree to the right is a Max-Heap. We may notice, it has duplicate values. However, this tree satisfies all the Max-Heap properties. This is a complete tree and every subtree contains values less or equal than its root node.
Talking about time complexities, we can build a Heap in time. But, there exists an algorithm, which allows building a Heap in
time. The insert and remove operations cost
. However, the Heap is an unordered data structure. The only possible way to get all its elements in sorted order is to remove the root of the tree
times. This algorithm is also called Heap Sort and takes
time.
4. Heap vs BST
The main difference is that Binary Search Tree doesn’t allow duplicates, however, the Heap does. The BST is ordered, but the Heap is not. So, if order matters, then it is better to use BST. If an order is not relevant, but we need to be sure that insert and remove will take time, then the Heap guarantees to achieve this time. In a Binary Search Tree, this may take up to
time, if the tree is completely unbalanced (chain is the worst case). Also, Heap can be built in linear time, however, the BST needs
to be created.
Java implements these structures with the PriorityQueue and the TreeMap. PriorityQueue is a Max-Heap by default. TreeMap has a balanced binary search tree as a backbone. Its implementation is based on a Red-Black Tree.
5. Conclusion
In this article, we’ve described two commonly used data structures: Heap and Binary Search Tree. We’ve talked about their structure and operations’ time complexities. Also, we’ve compared them and shown their pros and cons. These data structures have different areas of use. So, the choice depends on the problem.