Max-Heapify A Binary Tree

1. Overview

Heap is a special type of balanced binary tree data structure. A very common operation on a heap is heapify, which rearranges a heap in order to maintain its property.

In this tutorial, we’ll discuss a variant of the heapify operation: max-heapify. We’ll discuss how to perform the max-heapify operation in a binary tree in detail with some examples.

2. Definition of Heap

A heap or a binary heap is a complete binary tree with some additional properties, known as heap properties. Now before jumping into the heap properties, note that there are two variants of a heap: max-heap and min-heap. The heap properties change a bit with each variant.

Let’s first discuss the heap property for a max-heap. According to the heap property, the key or value of each node in a heap is always greater than its children nodes, and the key or value of the root node is always the largest in the heap tree.

The heap property for min-heap states that the value or key of each child node is always greater than its parent node, and the value of the root node is always the smallest in the heap.

Let’s look at some examples:

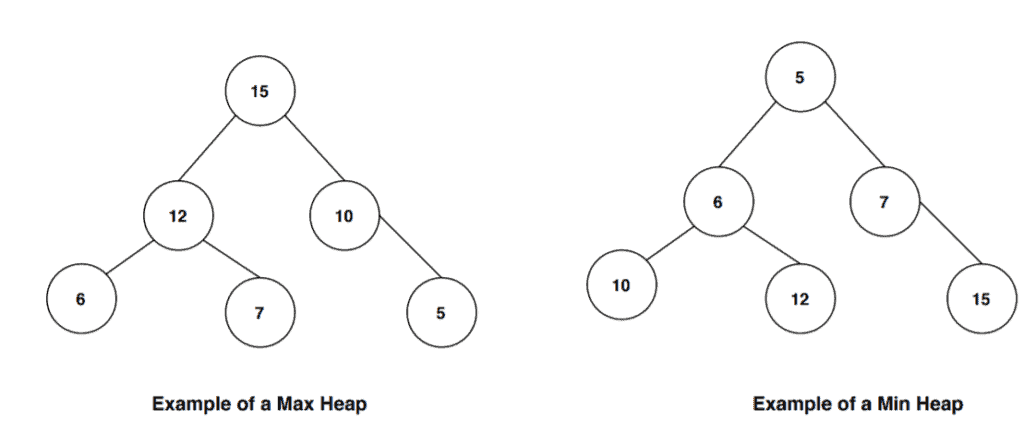
In the first tree, the root node is the highest valued key node among all the other nodes in the tree. Also, in all the subtrees, each parent node has the greater valued key then the children nodes. Therefore it follows the max-heap property.

In the second example, the root node is the smallest among all other nodes in the tree. We can also observe that each parent in the subtrees in this heap has a smaller value than their children nodes. Hence it satisfies the min-heap property.

3. Max-Heapify Operation

Max-heapify is a process of arranging the nodes in correct order so that they follow max-heap property. Let’s first see the pseudocode then we’ll discuss each step in detail:

algorithm MaxHeapify(B, s):
    // INPUT
    //    B = input array
    //    s = an index of the node
    // OUTPUT
    //    The heap tree that obeys max-heap property

    left <- 2 * s
    right <- 2 * s + 1

    if left <= B.length and B[left] > B[s]:
        largest <- left
    else:
        largest <- s

    if right <= B.length and B[right] > B[largest]:
        largest <- right

    if largest != s:
        swap(B[s], B[largest])
        MaxHeapify(B, largest)

We take an array and an index of a node as the input. The variable and denotes the left and right child node of the starting node .

We then arrange the node and its subtrees from the input array in such a way that it satisfies the max-heap property.

Using , we construct a max-heap. We start our algorithm with a node that is at the lowest level of the tree and has children node. We then arrange the current node and its children nodes according to the max-heap property.

Once we complete this step, we continue this process and make sure all the subtrees are following the max-heap property. Like this, we call recursively and iterate back to the root node and make sure the tree obeys the max-heap property.

Next let’s see how to build a heap from the input array. When the input array doesn’t obey the heap property, we call to build a heap and then we run on the constructed heap tree:

algorithm MaxHeapBuilding(B):
    // INPUT
    //    B = input array
    // OUTPUT
    //    Returns the heap tree corresponding to B
    
    n <- length(B)
    
    B.heapsize <- n
    
    for k <- n / 2, n / 2 - 1, ..., 1:
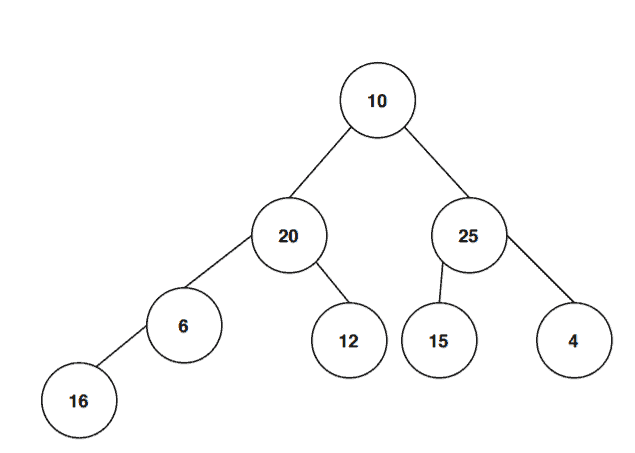
        MaxHeapify(B, k)

4. Max-Heapify Example

Lets take an input array . The first step is to create a binary tree from the array:

Now we’ll take a subtree at the lowest level and start checking whether it follows the max-heap property or not:

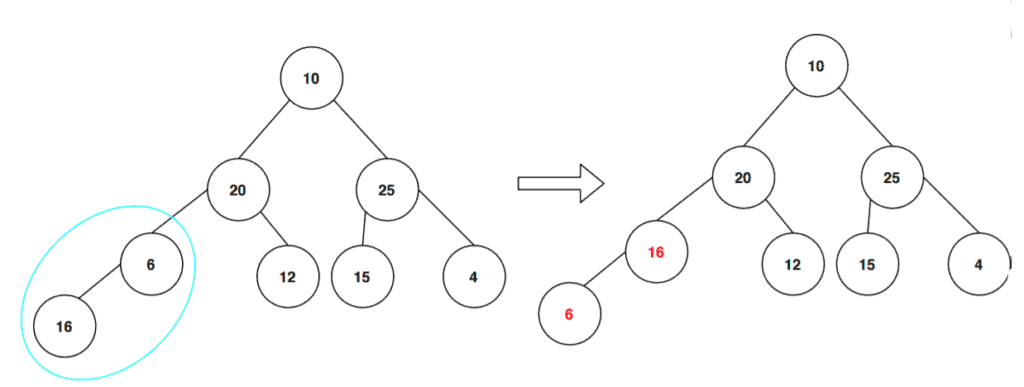
As we can see, the subtree doesn’t follow the max-heap property. Here, the parent node should contain a greater value than its children node. So in order to make sure that the tree follows the max-heap property, we swap the key values between the children node and the parent node.

Let’s continue and examine all the subtrees from the lowest level to the top level:

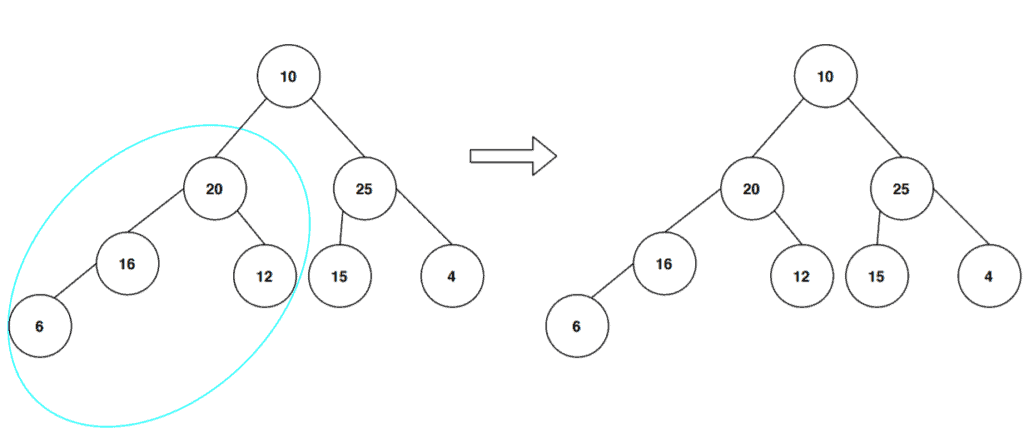
This subtree follows the max-heap property, and we don’t need to change anything here. Next, we look at the right side branches:

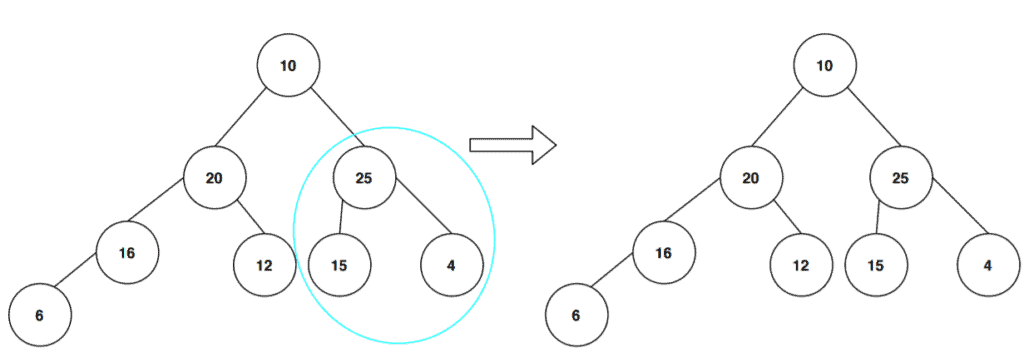
Again the subtree follows the max-heap property. Let’s continue this process:

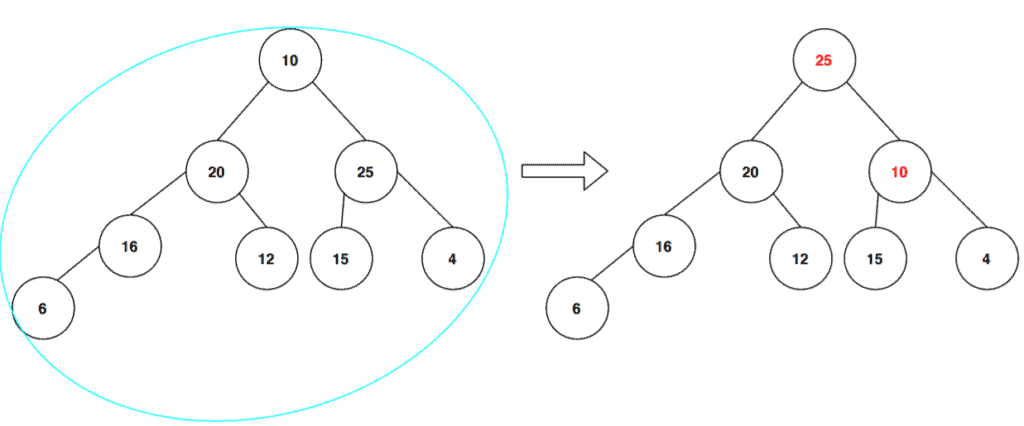
Here again, we can see that the key value of the root node is not the largest among all the nodes in the tree. Hence we swapped the key values of the root node with the key value of its right children node to match with the max-heap property.

Now, after the swap, we need to check the right subtree from the root node in order to see whether it follows the max-heap property or not:

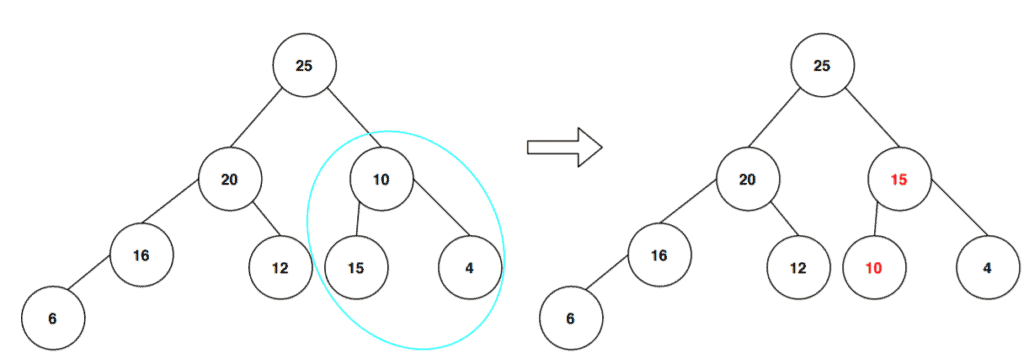
Finally, we’ve to check the whole tree in order to see if it satisfies the max-heapify property, and then we’ll get our final max-heap tree:

5. Conclusion

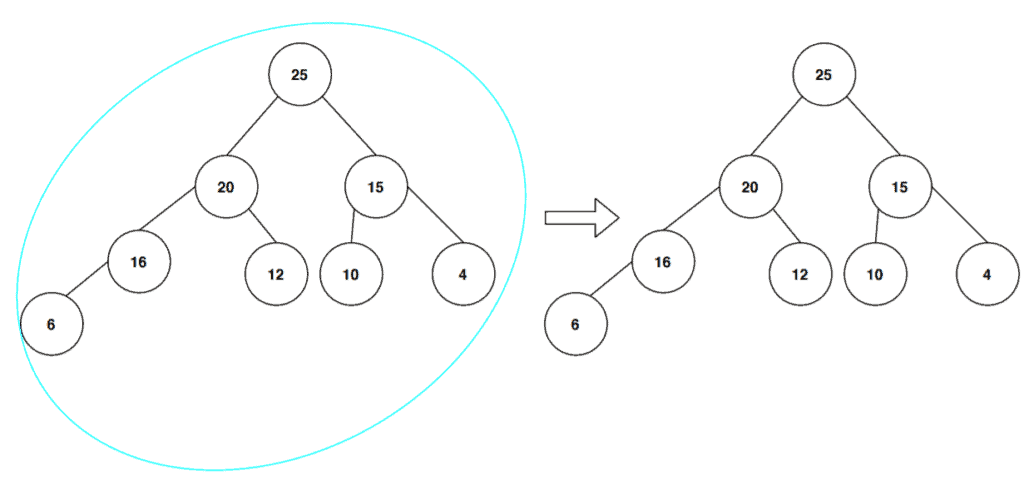
In this tutorial, we’ve discussed the process of max-heapify in a binary heap. We also presented an example of demonstrating how a max-heap is created from the input array.