1. Introduction
In this tutorial, we’ll study heuristics, metaheuristics, and probabilistic algorithms. We’ll focus on their definition, similarities, differences, and examples.
First, we’ll have a brief review on problem-solving and optimization problems in Computer Science, thus talking about the traditional techniques in these contexts. So, we’ll see particular concepts and features of heuristics, metaheuristics, and probabilistic algorithms. At last, we’ll compare them in a systematic summary.
2. Problem-solving in Computer Science
Essentially, we use computing to solve a myriad of real-world problems.
For instance, we can employ graph theory and algorithms to define the shortest path between two specific points. Furthermore, we can calculate the best allocation of items in a bag according to size and weight.
Both scenarios previously cited are classical optimization problems in Computer Science which we call “The Travelling Salesman” and “The Knapsack Problem”, respectively.
To solve these problems, we can adopt several different strategies. Some strategies solve only a problem, while others are adjustable to tackle multiple ones.
Moreover, some strategies may find in global optima results. Other strategies, in turn, provide sub-optimal but sufficiently good outcomes.
In the last case, we can classify problem-solving strategies as exact or non-exact. Let’s take a look at this classification in the following subsection.
2.1. Exact and Non-exact Strategies
As previously discussed, the categories of exact and non-exact regard the probability of a problem-solving strategy getting the optimal result.
In summary, exact algorithms guarantee (with 100% probability) the achievement of the optimal solution to a given problem. Strategies such as brute-force algorithms are always exact ones.
Furthermore, we can have supporting heuristics to exact algorithms. According to the problem, we can employ heuristics to avoid bad choices and test only (and all) the promising results.
However, exact algorithms may demand more computational resources and execution time than we have to solve a problem. In such cases, non-exact strategies are the best options.
In this scenario, we work with algorithms that do not guarantee the globally optimal result. However, non-exact algorithms explore the problem in an intelligent way, thus finding good results in a feasible time with fewer resources.
So, heuristics, metaheuristics, and probabilistic algorithms are non-exact strategies. Some examples are greedy search algorithms, tabu search, and evolutionary strategies.
In the following sections, we’ll particularly see concepts and examples of heuristics, metaheuristics, and probabilistic algorithms.
3. Heuristics
A heuristic is a strategy that uses information about the problem being solved to find promising solutions.
According to the chosen heuristic for a specific problem, the objective is not necessarily finding the optimal solution but only finding a good enough solution. Heuristics based on greedy search are in this class, for example.
Other times, we can use heuristics not to find a result but to discard obviously bad results. In such a case, heuristics remove portions of the search space and test all the remaining possible results. We call these heuristics supporting heuristics.
Regardless of which heuristic we adopt, they have some common characteristics:
- Problem-based design: heuristics are tailored to a particular problem. In this way, a single heuristic often can solve only one problem, and nothing more (one-to-one relation)
- Non-measurable success: different from approximate algorithms, heuristics don’t provide a clear indication of how close (or far) the obtained result is to the optimal one
- Reasonable execution: the time or computational resources for executing a heuristic must never exceed the requirements of any exact method that solves the same problem
The following image depicts how an exact, supporting heuristic and greedy search-based heuristic tackles a simple traveling salesman problem:
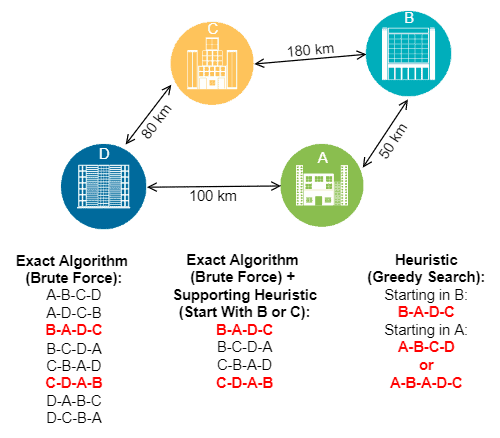
In the image above, the final results are in red. So, the exact algorithm always gives globally optimal results. The exact algorithm with the supporting heuristic also found globally optimal results. At last, the heuristic may return the globally optimal result, but it depends on the parameters provided for the execution.
4. Metaheuristics
Similar to heuristics, metaheuristics aim to find promising results for a problem. However, the algorithm used for a metaheuristic is generic and can deal with different problems.
In this way, the characteristics of “non-measurable success” and “reasonable execution” are still the same as discussed for the heuristics. However, metaheuristics replace the principle of the problem-based design with the problem-independent design:
- Problem-independent design: the possibility of using the same metaheuristic algorithm to solve a myriad of problems by just tuning its inputs
Famous examples of metaheuristics are genetic algorithms, particle swarm optimization, simulated annealing, and variable neighborhood search. However, of course, there exist many more.
Moreover, according to how a metaheuristic works to find results for a problem, we can divide them into three categories:
- Local search metaheuristics: also known as iterative improvement, metaheuristics in this category find a good final result by iteratively improving a single intermediate result
- Constructive metaheuristics: instead of solving entire problems at one time, constructive metaheuristics break a problem into multiple subproblems, solve each one of them and merge the partial results to provide a complete result
- Population-based metaheuristics: this category of metaheuristics considers a population of potential results for a given problem, thus improving these potential results by combining and modifying them
The following image shows a simple example of a traveling salesman problem being solved with a genetic algorithm, which is a population-based metaheuristic:
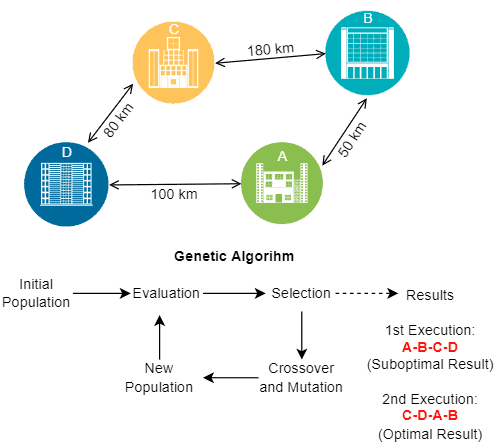
It is relevant to note that, in the specific case of a genetic metaheuristic, we can not infer the results by the inputs since there are stochastic operations to define when and how the intermediary results combine and modify.
5. Probabilistic Algorithms
We already talked about heuristic and metaheuristic algorithms which sacrifice the certainty of finding the optimal result to produce good enough results with feasible time and computational resources.
Moreover, we briefly discussed exact (also known as deterministic) algorithms that always return the optimal result for a given problem.
Probabilistic algorithms, in turn, are a class of non-exact strategies for problem-solving. However, unlike heuristics and metaheuristics, probabilistic algorithms are designed to get the optimal result.
But, probabilistic algorithms have only a high probability of finding the optimal result in a feasible time. So, these algorithms guarantee neither the optimal result nor a reduced execution time to find it.
It occurs because probabilistic algorithms employ some random elements. Thus, depending on the definition of these random elements in each execution, we can transform a complex problem into a simple one or an intractable one.
There exist three main categories of probabilistic algorithms:
- Monte Carlo: we fastly find a result, but it may not be correct or the optimal one
- Las Vegas: we find the optimal or correct result, but it is not guaranteed to be fast to do it
- Sherwood: we always find the optimal or correct result, and the random factor avoids us doing that by taking the worst-case execution scenario
5.1. A Simple Monte Carlo Example
Let’s consider a list of numbers and a Monte Carlo algorithm to check if there is a majority element (at least 50% + 1 occurrence) in that list. The algorithm selects a random number from the list and checks its occurrences, returning true if it is the majority number or false if it is not.
The pseudocode of the described algorithm follows:
algorithm MonteCarloMajority(numberList, lengthList):
// INPUT
// numberList = a list of numbers
// lengthList = the length of numberList
// OUTPUT
// Returns true if a randomly selected number appears more than lengthList / 2 times,
// and false otherwise
i <- RANDOM() mod lengthList
// RANDOM() returns a random number
j <- 0
c <- 0
while j < lengthList:
if numberList[i] = numberList[j]:
c <- c + 1
j <- j + 1 return c > lengthList / 2So, if there is a majority element, the probability of returning a wrong result is less than . In this way, if we run this algorithm N times and always get false as a result, we improve its confidence and the probability of it being wrong decreases to
.
Of course, there is always a chance that a majority number exists. But, as the number of executions increases and we do not find this majority number, the probability of it existing turns negligible.
6. Systematic Summary
Nowadays, we use computer systems to solve multiple problems. Some problems are simple in terms of the currently available computing capabilities. In this case, we can employ exact algorithms to solve these problems, getting optimal results.
However, other problems are too complex to be solved with exact algorithms in a feasible time and using a reasonable amount of computational resources. So, we can use other classes of strategies to solve them. Examples are heuristics, metaheuristics, and probabilistic algorithms.
These other classes of algorithms can find the optimal result to a problem, like exact algorithms, but it is not guaranteed. However, these algorithms are faster and usually consume less computational resources than the exact alternatives.
The table below summarizes the characteristics of exact, heuristic, metaheuristic, and probabilistic algorithms.
7. Conclusion
In this tutorial, we studied heuristics, metaheuristics, and probabilistic strategies. At first, we briefly reviewed problem-solving in the context of computing. So, we specifically explored the characteristics of heuristics, metaheuristics, and probabilistic algorithms. Finally, we compared some characteristics of these different algorithm classes in a systematic summary.
We can conclude that non-exact strategies are crucial for solving computational problems. However, there are complex problems, and using exact algorithms to solve them is unfeasible. Thus, heuristics, metaheuristics, and probabilistic algorithms become viable options for solving these complex computational problems.