1. Introduction
In this tutorial, we’ll talk about the kernel type for an SVM. We’ll show how to choose the most suitable kernel. We’ll present a discussion about the advantages and disadvantages of each Kernel type.
2. What Are Kernel Functions?
The SVM algorithm uses a set of mathematical functions defined as kernels. A kernel function is a method that takes data as input and transforms it into the needed form. In other words, the kernel function converts the training data set to convert the nonlinear decision surface into a linear equation in a higher dimensional space.
3. Which Factors to Consider When Selecting a Kernel?
The choice of selecting the kernel in SVM depends on the type of problem. Indeed, considering the nature of the problem we are trying to solve, such as linear or nonlinear classification, anomaly detection, or regression, different kernels may be a choice for each.
If you are dealing with linear classification problems, a linear kernel may be appropriate since it is effective in separating data that can be linearly separated. However, when faced with nonlinear classification problems, it becomes necessary to consider utilizing nonlinear kernels like radial basis function (RBF), polynomial, or sigmoid kernels. These kernels can handle decision boundaries that are more intricate and complex.
Furthermore, it is of utmost importance to consider the selection of a kernel when working with regression tasks or anomaly detection. In the case of regression tasks, the decision regarding which kernel to utilize can significantly influence the model’s capacity to comprehend the fundamental connections between the input and output variables. As for anomaly detection, the task often necessitates the identification of intricate patterns within the data, making a nonlinear kernel a more fitting choice.
4. How to Select the Right Kernel
Choosing the right kernel is crucial for various ML algorithms, especially SVM. To choose the right kernel in SVM, we have to take into consideration the type of problem, the computational complexity, and the characteristics of the data. We present in this section some examples of choosing the right kernel for an SVM problem.
4.1. Linear Kernel
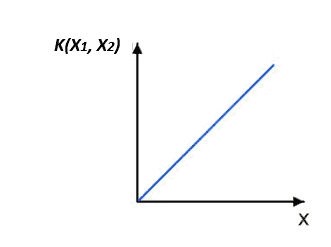
We use Linear kernels when the number of features is large compared to the number of samples or when the data are linearly separable. Linear kernels’ suite for problems of text classification, document classification, and other high-dimensional data. The linear kernel can be expressed as:
The linear kernel has the following form:
4.2. Radial Basis Function Kernel (RBF)
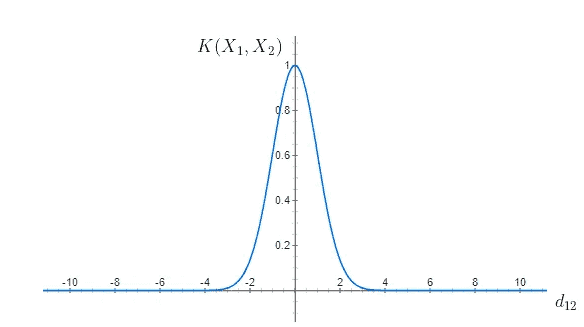
The RBF kernel is suitable for nonlinear problems and is the default choice for SVM. It’s powerful when there is no prior knowledge of the data, and we can capture complex relationships between data points. The RBF kernel can be expressed as:
The RBF kernel has the following form:
4.3. Polynomial Kernel
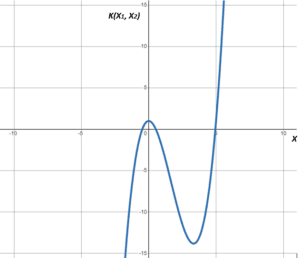
Polynomial kernels are useful when treating problems that show polynomial behavior. They are commonly used for computer vision and image recognition tasks. We express the polynomial kernel as:
The polynomial kernel can have many forms. Here, we present one form of the polynomial kernel:
4.4. Sigmoid Kernel
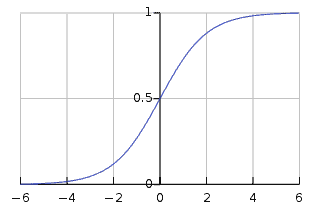
We use a sigmoid kernel when dealing with neural network applications and when we know that the data distribution looks like a sigmoid function. We express the sigmoid kernel as:
=
The sigmoid kernel has the following form:
4.5. Customized Kernel
Sometimes, custom kernels tailored to specific domain knowledge or problem characteristics can outperform standard kernels. For example, designing kernels based on domain-specific similarity measures can improve performance. In this type of kernel, we don’t have a generic form of kernel because this kernel is tailored according to a specific domain.
Nowadays, grid search and cross-validation techniques can also help determine the best-performing kernel for a given dataset.
5. Advantages and Disadvantages of Each Kernel Type
Here is the summary table of advantages and disadvantages of each Kernel type:
| Kernel Type | Advantages | Disadvantages |
|---|---|---|
| Linear | Computationally efficient – Works well for high-dimensional data | Limited to linearly separable data – May not capture complex relationships in nonlinear data |
| Radial Basis Function (RBF) | Effective for capturing complex nonlinear relationships | Can be sensitive to overfitting |
| Polynomial | It is useful for problems with polynomial behavior and can also capture nonlinear relationships in the data | Prone to overfitting in high-degree polynomials, It is sensitive to the choice of degree parameter |
| Sigmoid | Can be effective in specific applications, such as neural networks | Limited applicability compared to other kernels |
| Custom Kernels | Tailored to specific domain knowledge or problem characteristics | Designing custom kernels requires domain expertise and experimentation |
6. Conclusion
In this article, we talked about the kernel type for an SVM. Overall, to consider the selection of a kernel in SVM, we need to know the nature of the problem we are trying to solve, such as linear or nonlinear classification, anomaly detection, or regression.