1. Introduction
The Support Vector Machine (SVM) algorithm is a popular machine learning algorithm that is commonly used for classification and regression tasks. It works by finding an optimal hyperplane that separates different classes or predicts continuous values based on labeled training data.
One of the most important parameters in the SVM is the parameter, which plays a crucial role in determining the balance between achieving a low training error and allowing for misclassifications.
In this tutorial, we’ll explore in-depth the parameter in SVM.
2. Overview
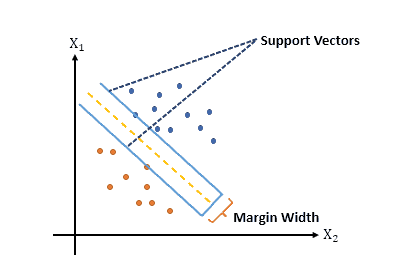
To grasp the significance of parameter , we should first understand how the margin concept works in SVM. The margin refers to the maximum width of the boundary that we can draw between the classes.
SVM aims to find a hyperplane that maximizes this margin, as it tends to generalize better on unseen data. In addition, the support vectors control the margin width, which are the data points closest to the decision boundary.
The following figure shows the concept of the margin in SVM:
3. The Role of C in SVM
The parameter in SVM helps control the trade-off between the training error and the margin since it can determine the penalty for misclassified data points during the training process.
To be specific, a smaller value of allows for a larger margin, potentially leading to more misclassifications on the training data. On the other hand, a larger value of
puts more emphasis on minimizing the training error, potentially leading to a narrower margin.
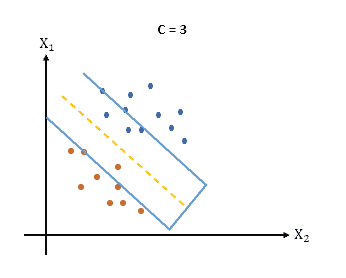
3.1. Small C Value and Large Margin
When the value of is small, the SVM algorithm focuses more on achieving a larger margin. In other words, a smaller
value allows for more misclassifications in the training data, which can result in a wider margin between the classes.
Note that this can be useful in scenarios where the data points are well-separated, and there is a low presence of noise or outliers. However, it is important to be cautious as setting too small can lead to underfitting, where the model fails to capture the underlying patterns in the data.
The following figure provides a visual representation of the effect of a small value on the margin:
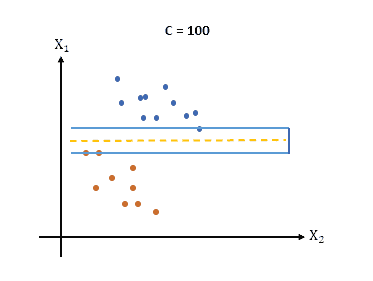
3.2. Large C Value and Narrow Margin
Conversely, a larger value of in SVM emphasizes minimizing the training error, potentially resulting in a narrower margin. When
is set to a large value, the SVM algorithm seeks to fit the training data as accurately as possible, even if it means sacrificing a wider margin.
Remember that this can be beneficial when the data points are not well-separated or when there is a significant presence of noise or outliers. However, setting too large can increase the risk of overfitting, where the model becomes too specific to the training data and performs poorly on new, unseen data.
The following figure visually illustrates the impact of a large value on the margin:
4. Selecting the Optimal Value of C
Selecting the optimal value of is crucial for achieving the best performance of an SVM model. Moreover, the choice of
depends on the specific problem we are trying to solve, the dataset, and desired trade-offs between training error and margin width.
There are several approaches to determining the optimal value of C:
4.1. Grid Search
Grid Search is a commonly used technique to tune hyperparameters. It involves defining a grid of potential values and evaluating the performance of the SVM model for each combination of
values using cross-validation.
We can select the value that yields the best performance metric, such as accuracy or F1 score, as the optimal solution.
4.2. Randomized Search
Randomized Search is an alternative to Grid Search that randomly samples different values of from a specified distribution. This technique is useful when the hyperparameter search space is large, and an exhaustive search is computationally expensive.
An optimal value can be approximated by evaluating the model’s performance for a subset of randomly chosen values.
4.3. Bayesian Optimization
Bayesian optimization is a sequential model-based optimization technique that uses probabilistic models to guide the search for optimal hyperparameters. It efficiently explores the hyperparameter search space by iteratively evaluating the SVM model’s performance and updating the probabilistic models.
Bayesian optimization can effectively handle high-dimensional hyperparameter spaces and requires fewer evaluations compared to many exhaustive search methods.
4.4. Metaheuristic Algorithms
Metaheuristic algorithms, such as Genetic Algorithm (GA) or Particle Swarm Optimization (PSO), mimic natural processes of evolution or collective behavior. It’s main goal is to efficiently explore the search space in order to find near-optimal solutions.
Note that these algorithms can also be utilized to find the optimal value of .
4. Conclusion
In conclusion, the parameter in the SVM algorithm plays a vital role in determining the trade-off between training error and margin width. It controls the penalty for misclassified points during training, affecting the generalization performance and the potential for overfitting or underfitting.
Furthermore, selecting an appropriate value for is crucial for achieving a well-performing SVM model. Hence, hyperparameter tuning techniques, such as cross-validation or metaheuristic algorithms, maybe a good way to find the near-optimal value of
.