Cross-Validation: K-Fold vs. Leave-One-Out

Last updated: March 18, 2024

Reviewed by: Milos Simic 


1. Overview




In this tutorial, we’ll talk about two cross-validation techniques in machine learning: the k-fold and leave-one-out methods. To do so, we’ll start with the train-test splits and explain why we need cross-validation in the first place. Then, we’ll describe the two cross-validation techniques and compare them to illustrate their pros and cons.


2. Train-Test Split Method




An important decision when developing any machine learning model is how to evaluate its final performance. To get an unbiased estimate of the model’s performance, we need to evaluate it on the data we didn’t use for training. 


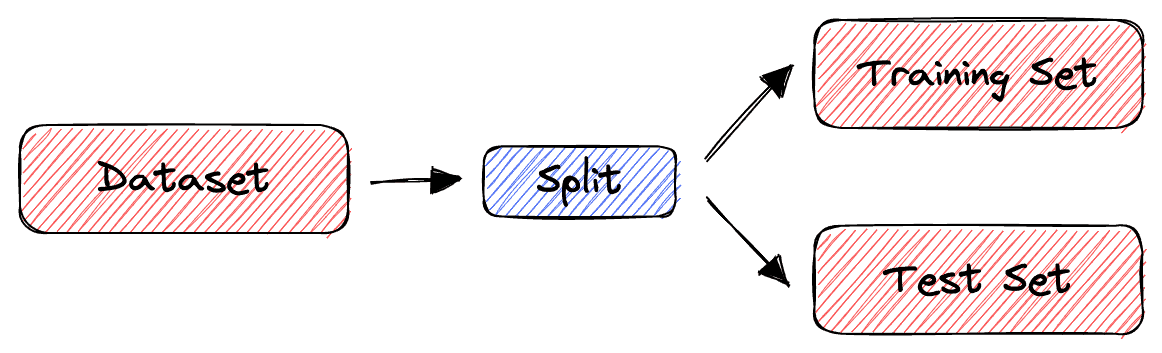
The simplest way to split the data is to use the train-test split method. It randomly partitions the dataset into two subsets (called training and test sets) so that the predefined percentage of the entire dataset is in the training set.


Then, we train our machine learning model on the training set and evaluate its performance on the test set. In this way, we are always sure that the samples used for training are not used for evaluation and vice versa.


Visually, this is how the train-test split method works:







 

train-test split

3. Introduction to Cross-Validation




However, the train-split method has certain limitations. When the dataset is small, the method is prone to high variance. Due to the random partition, the results can be entirely different for different test sets. Why? Because in some partitions, samples that are easy to classify get into the test set, while in others, the test set receives the ‘difficult’ ones.


To deal with this issue, we use cross-validation to evaluate the performance of a machine learning model. In cross-validation, we don’t divide the dataset into training and test sets only once. Instead, we repeatedly partition the dataset into smaller groups and then average the performance in each group. That way, we reduce the impact of partition randomness on the results.


Many cross-validation techniques define different ways to divide the dataset at hand. We’ll focus on the two most frequently used: the k-fold and the leave-one-out methods.


4. K-Fold Cross-Validation




In k-fold cross-validation, we first divide our dataset into k equally sized subsets. Then, we repeat the train-test method k times such that each time one of the k subsets is used as a test set and the rest k-1 subsets are used together as a training set. Finally, we compute the estimate of the model’s performance estimate by averaging the scores over the k trials.







For example, let’s suppose that we have a dataset S = \{x_1, x_2, x_3, x_4, x_5, x_6\} containing 6 samples and that we want to perform a 3-fold cross-validation.


First, we divide S into 3 subsets randomly. For instance:


S_1 = \{x_1, x_2\}

S_2 = \{x_3, x_4\}

S_3 = \{x_5, x_6\}


Then, we train and evaluate our machine-learning model 3 times. Each time, two subsets form the training set, while the remaining one acts as the test set. In our example:

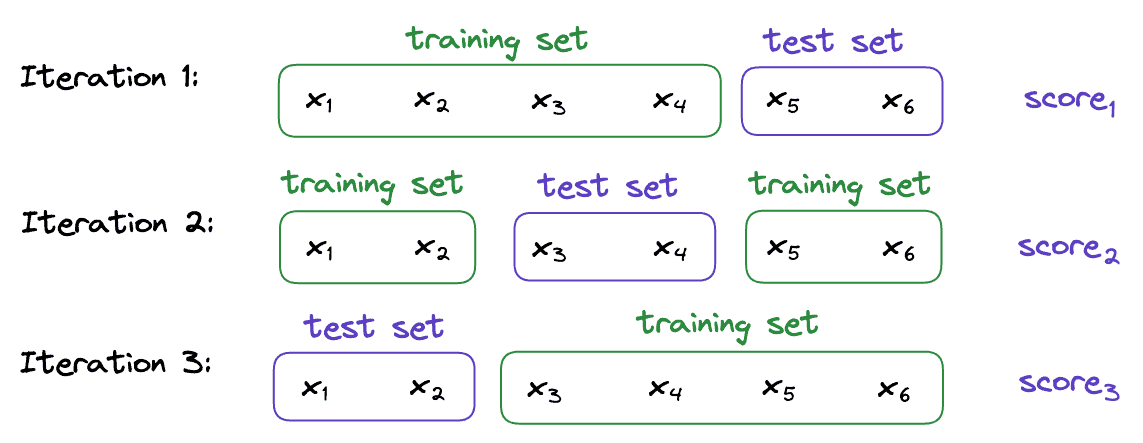
k-fold cross validation


Finally, the overall performance is the average of the model’s performance scores on those three test sets:







      \[\text{overall score} = \frac{score_1 + score_2 + score_3}{3}\]


5. Leave-One-Out Cross-Validation




In the leave-one-out (LOO) cross-validation, we train our machine-learning model n times where n is to our dataset’s size. Each time, only one sample is used as a test set while the rest are used to train our model.


We’ll show that LOO is an extreme case of k-fold where \mathbf{k=n}. If we apply LOO to the previous example, we’ll have 6 test subsets:


S_1 = \{x_1\}

S_2 = \{x_2\}

S_3 = \{x_3\}

S_4 = \{x_4\}

S_5 = \{x_5\}

S_6 = \{x_6\}


Iterating over them, we use S \setminus S_i as the training data in iteration i=1,2,\ldots, 6, and evaluate the model on S_i:

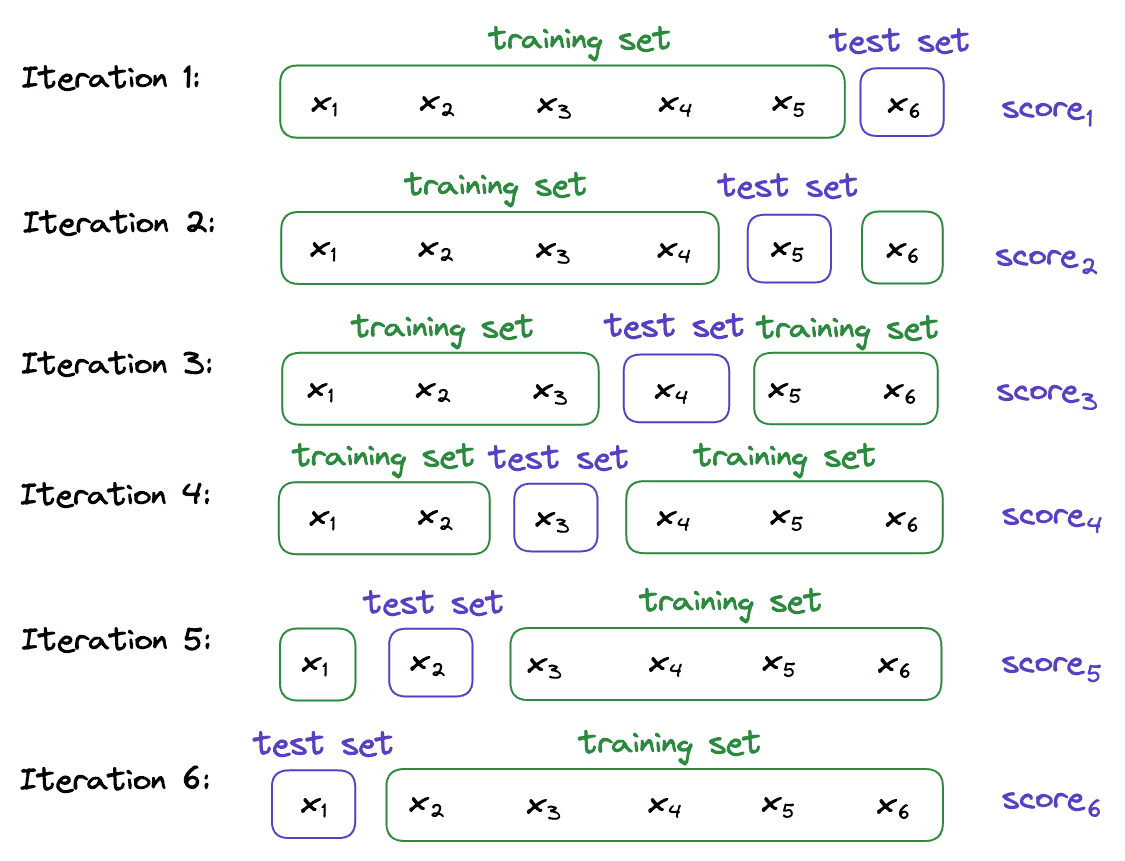
leave-one-out (LOO) cross-validation


The final performance estimate is the average of the six individual scores:


      \[\text{overall score} = \frac{score_1 + score_2 + score_3 + score_4 + score_5 + score_6}{6}\]


6. Comparison




An important factor when choosing between the k-fold and the LOO cross-validation methods is the size of the dataset.







When the size is small, LOO is more appropriate since it will use more training samples in each iteration. That will enable our model to learn better representations.


Conversely, we use k-fold cross-validation to train a model on a large dataset since LOO trains n models, one per sample in the data. When our dataset contains a lot of samples, training so many models will take too long. So, the k-fold cross-validation is more appropriate.


Also, in a large dataset, it is sufficient to use less than n folds since the test folds are large enough for the estimates to be sufficiently precise.


7. Conclusion




In this article, we presented two cross-validation techniques: the k-fold and leave-one-out (LOO) methods. The latter validates our machine learning model more times giving us very precise metrics. However, in the case of large datasets, the k-fold cross-validation will give us sufficiently precise estimates but will spend less time training the model.


 

 






    


Comments are open for 30 days after publishing a post. For any issues past this date, use the Contact form on the site.