1. Introduction
Data structures are essential components of computer science that allow for efficient data storage and retrieval. One of the most powerful data structures in this regard is the randomized search tree (RST).
In this tutorial, we’ll learn about RSTs and their implementation and advantages over other data structures.
2. Overview
An RST is a binary search tree in which the order of the nodes is randomized. RSTs combine the advantages of binary search trees and hash tables, making them ideal for applications where fast searching and insertion are crucial.
Like other binary search trees, RSTs are composed of nodes with left and right child. However, unlike traditional binary search trees, the nodes in an RST are randomly sorted.
RSTs are used in various applications, including databases, search engines, and computer graphics. They are particularly useful in applications that require fast performance and real-time updates. For example, RSTs can be used in web search engines to store and update the index of web pages. RSTs can also be used in computer graphics to store and update the positions of objects in a scene.
3. Implementation of RSTs
We can use an RST as a binary search tree, where each node has a key, a value, and a randomly assigned priority that is used to maintain the order of the tree. The priority is assigned randomly when the node is created, and it is used to maintain the order of the tree. The tree is organized such that the left subtree of any node contains only nodes with keys less than that of the node, and the right subtree contains only nodes with keys greater than that of the node.
Let’s look into different operations that we can perform on RSTs.
Insertion involves finding the correct position for a new node based on its key and priority and then inserting it into the tree. We first check if the RST is empty to insert a new node. If the RST is empty, we create a new node and make it the tree’s root. Otherwise, we insert the new node in the correct position based on its key and priority.
To insert a new node in the correct position, we start at the root node and compare the new node’s key with the current node. If the key of the new node is less than the current node’s key, we move to the left child; otherwise, to the right child of the current node. We continue this process until we find an empty spot to insert the new node.
However, unlike standard binary search trees, RSTs require an additional random priority value to be associated with each node. This priority value is generated randomly during insertion and balances the tree during subsequent operations. The priority value of the root node is always greater than the priority values of its children, and the priority values of the left subtree are always less than the priority values of the right subtree.
For example, let’s say we want to insert the node with key 25 and priority 2 into the initial RST in the diagram below:
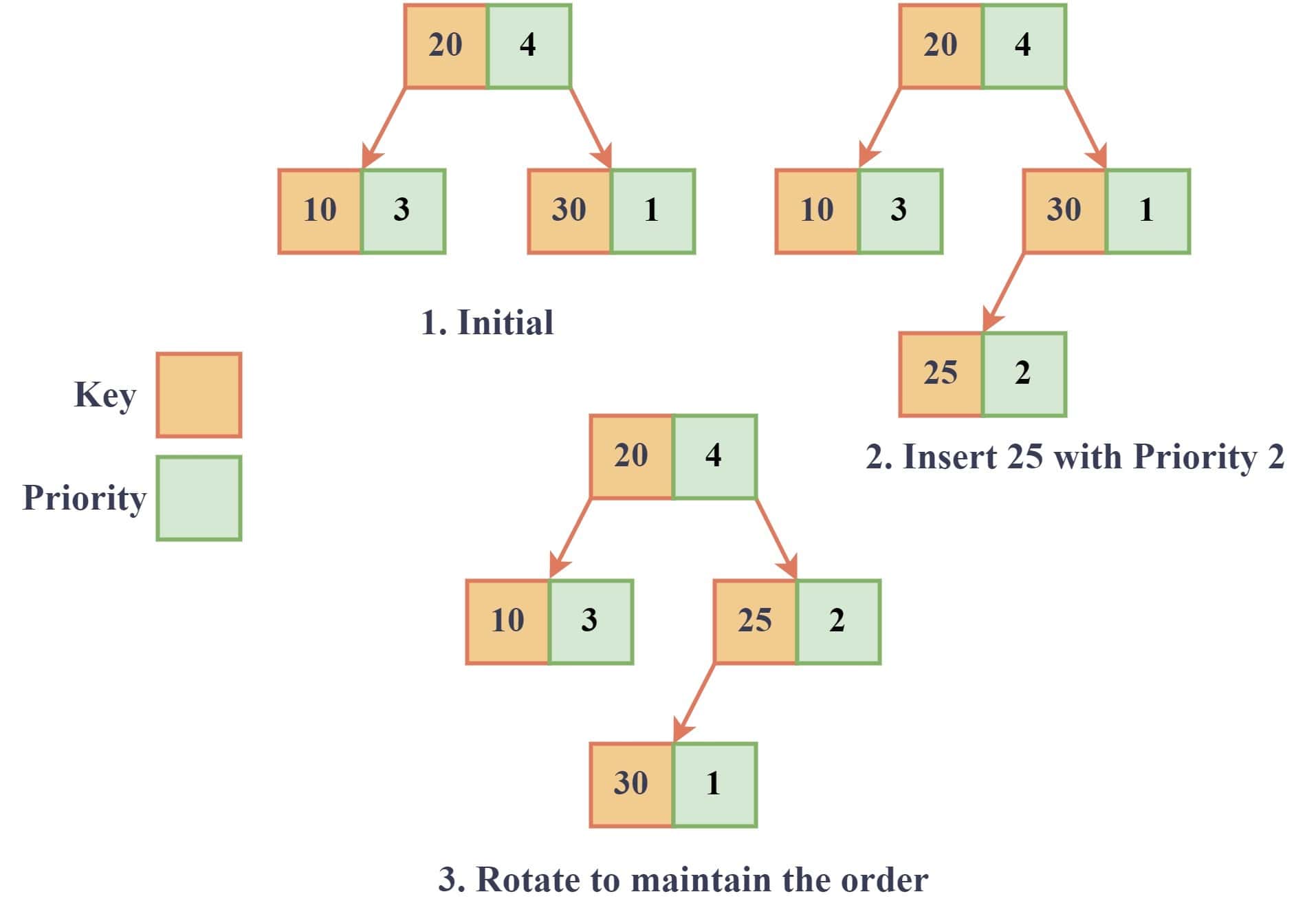
First, we start at the root node (20,4) and compare the key of the new node (25) with the key of the current node (20). Since 25 is greater than 20, we move to the right child (30,1). Since the right child is a leaf node, we create a new node with key 25 and priority 2 as its child.
Now we need to perform rotations to maintain the order of the tree. The right child (30,1) has a lower priority than its right grandchild (25,2), so we perform a left rotation. After this, we can see that the priorities of the nodes are in the correct order, and the RST is balanced.
The deletion algorithm for RSTs is similar to that of a standard binary search tree. We first search for the node to be deleted and then perform one of the following cases:
- If the node has no children, we delete the node.
- If the node has one child, we replace the node with its child.
- If the node has two children, we replace the node with its successor and delete the successor.
However, unlike standard binary search trees, we also need to maintain the priority values of the remaining nodes during deletion. We do this by swapping the node to be deleted with its child with the highest priority value. We then continue deleting the node in the swapped position until we reach a node with no children.
3.1. Algorithm
Let’s take a look at the pseudocode for the insertion and deletion of a value into RSTs.
We have incorporated subroutines for the left and right rotation functions within the pseudocode above.
Now, for the deletion of a value:
Note that we only need to do rotations during deletion if the node to be deleted has two children. If it only has one child or no children, we can remove it from the tree without needing to do any rotations.
4. Time Complexity Analysis
RSTs provide average-case performance guarantees for search, insertion, and deletion, even under worst-case scenarios. The average case time complexity of operations in an RST is , where n is the number of nodes in the tree.
The randomness of the node order in an RST allows for average-case performance guarantees. This time complexity is the same as other balanced binary search trees such as AVL and Red-Black trees. However, RSTs have a better worst-case time complexity of than AVL trees and Red-Black trees, which have a worst-case time complexity of
and
, respectively.
5. Advantages of RSTs
RSTs have several advantages over other data structures, including:
- Randomization: The randomization in RSTs ensures that the tree remains balanced regardless of the order in which nodes are inserted or deleted. This makes RSTs suitable for real-time applications
- Memory Efficiency: RSTs use less memory than other balanced search trees because they do not store balance information at each node
- Performance: RSTs have better worst-case time complexity than AVL trees and Red-Black trees, which makes them better suited for applications that require fast performance
6. Conclusion
In this tutorial, we covered the basics of RSTs, including their structure and basic operations such as insertion and deletion.
One of the critical advantages of RSTs is their fast average-case performance. The time complexity of basic operations is average ), making RSTs an efficient solution for many search problems.