Learn through the super-clean Baeldung Pro experience:
>> Membership and Baeldung Pro.
No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.
Last updated: March 18, 2024
In this tutorial, we’ll discuss the subject of selection bias in statistical sampling and the techniques for limiting it.
Selection bias is a type of bias that’s common in statistical analysis and machine learning alike. It can lead to errors in predictive models due to distortions in the data that we use to train them.
The story that’s commonly told when introducing the problem of selection bias relates to the work of a famous mathematician, Dr. Wald. During the war, Wald was tasked by the American Navy to study the problem of minimizing casualties in air battles.
Dr. Wald first took a list of the areas that were more frequently repaired for damages after each battle. He then determined that, counter-intuitively, the areas that were reported as being more prone to damages were the strongest areas in the chassis of an aircraft. He, therefore, suggested strengthening the parts of the aircraft that did not receive maintenance after the battles.
His colleagues disagreed with him, and understandably so. After all, how could someone claim that the most frequently damaged parts of an aircraft were the most durable? If they’re damaged very often, then certainly they’re not durable at all, or are they?
Wald argued that, for an aircraft to be repaired by a mechanic in the first place, the aircraft had to survive the battle and reach the hangar safely. Not all aircraft did, and those that were too severely damaged would end up destroyed. Indeed, all aircraft that took damage in the areas not listed for maintenance, such as the cockpit or the wing engines, were those that the enemy had downed:
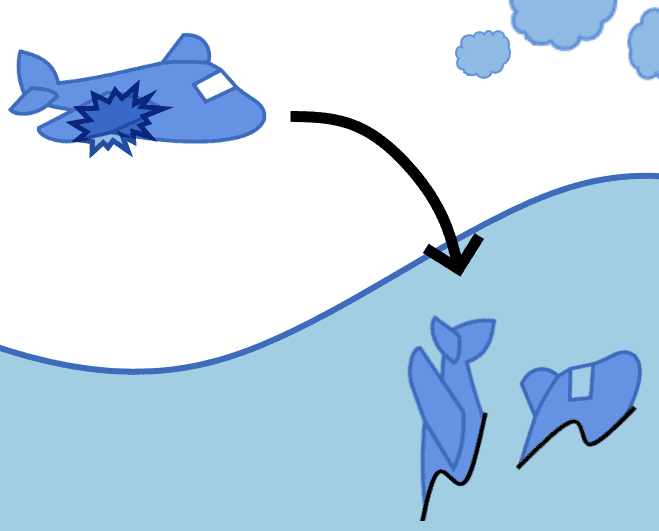
This short story introduces us to the problem of selection bias. The procedure for selecting a statistical sample could introduce a distortion in the statistic that we compute over that sample. If this is the case, the conclusions that we draw by analyzing it will also be affected by the same bias.
A less-famous story concerns an American man from Florida, who became famous a few years ago for winning several lottery extractions in a row. In a series of interviews released by ABC News, as well as in a book that he wrote, the lottery player recommended people his secret recipe for success. “Buy lottery tickets”, he said; and if you win then “use the lottery money all the time to buy more tickets”.
We can conceptualize the decision-making process which he advocated with a flowchart:
Indeed, this strategy and his secret recipe functioned, at least for him. They led him to acquire more than one million dollars in total profits over the course of around ten years.
But more interestingly, he isn’t the only one who won by applying this strategy. There is in fact a conspicuous number of people who applied it concretely, and who have indeed obtained large earnings.
Therefore, we could argue, it’s a good idea to invest our savings in lottery tickets. After all, plenty of observational cases suggests that people do indeed win big.
There has to be an error in this line of thought. But where exactly?
The reason why the previous strategy is unadvisable is not that it leads to sure losses: indeed, some people do become millionaires by applying it. But rather, the problem has to do with focusing on the cases where the observations satisfy our preconceptions and the exclusion of any cases which contradict our expectations.
By considering only the words of those who successfully applied this particular strategy, we’re misled into thinking that its odds are favorable. We could therefore believe, in Bayesian terminology, that the a priori probability of success is significantly high. And of course, we’d be wrong.
These considerations tell us that, according to the method which we use to select the observations upon which we conduct our analyses, we may get an understanding of reality that’s grossly incorrect.
The choice of examples that correspond to successful outcomes of a betting method is a kind of selection bias. More specifically, if the book’s author of the previous example received letters only from persons who applied that method successfully, and did not instead choose to voluntarily discard the complaints against his strategy, we’d be talking instead about survivor bias.
The reason for the latter is that, while a larger number of persons is expected to have applied the strategy than the number of persons who obtained profits, we can imagine that only the winners found a reason to write to the author out of gratitude. The remaining people, considering how they had already lost $10, may decide instead to simply cut their losses and not pay for the postal stamps required to send a letter.
These considerations tell us that selection bias isn’t a problem that concerns the phenomenon that we’re studying. Rather, it depends upon the choices of the statistician or the research that they conduct. If we, personally, do statistical analysis, then we’re the ones responsible for staying alert and preventing it.
Now that we understand what selection bias is and how it can influence our statistical analysis, it’s time to consider what methods are available to prevent it. In some cases full prevention may be impossible: in that case, reducing it to the largest extent possible is appropriate.
The first method we can use is the application of the principle of good practice in scientific research, which implies having updated knowledge on the subject that we study. Concretely, it’s customary to begin research with a review of the literature on the phenomenon that we’re analyzing.
Let’s assume, for example, that we’re studying the level of schooling and education in a population by administering questionnaires. We should expect the government organizations in the relevant country to have compiled reports in the past concerning the same topic. These reports, together with more properly scientific sources, would constitute the prior knowledge that we bring into the study.
The second method consists of the application of an observational or sampling methodology that’s appropriate for the phenomenon that we study. If we’re still interested in learning about educational achievements, and we administer written questionnaires to the population about the self-reported level of education, we’re certain to introduce selection bias to our study. In fact, each and every illiterate person is, by definition, unable to answer the written questionnaires by reason of their inability to read.
It can also happen that, for a particular population, its individuals can be grouped into clusters that are very similar to one another. In those cases, it’s appropriate to use techniques for random and stratified sampling.
The idea behind stratified sampling is that, if some populations can be divided into internally-homogeneous groups, then the statistical sample that we analyze should contain individuals that belong to those groups, in proportion to the group’s weight over the total population.
And finally, as a general rule, when doing statistical analyses we should always go with the Bayesian motto: “Know thyself, and know thy priors.” If we have a clear idea of the research hypotheses that we embed in our study, and if we also have a good idea of the a priori distribution that we should expect to observe, we’re much more likely to spot selection bias in our work.
This would in fact emerge as a gross and systematic deviation from the theoretical a priori distribution, that can’t be explained by statistical fluctuation.
In this article, we’ve studied the methods for preventing selection bias when we conduct statistical analysis.