Stratified Sampling in Machine Learning

1. Introduction

In this tutorial, we’ll review Stratified Sampling, a technique used in Machine Learning to generate a test set. Then we’ll illustrate how to implement it, and provide an example of an application.

2. Sampling Techniques

Creating a test set is a crucial step when evaluating a machine learning model. The simplest way to create a test set is to pick some instances randomly from a large dataset, typically 20% of the original dataset. In statistics, this method is called Simple Random Sampling, since a subset of instances (the sample) is chosen randomly from a larger set (the population). Each subset of instances has the same probability of being picked as a sample as any other subset of elements.

Random sampling is generally fine if the original dataset is large enough; if not, a bias is introduced due to the sampling error. Stratified Sampling is a sampling method that reduces the sampling error in cases where the population can be partitioned into subgroups. We perform Stratified Sampling by dividing the population into homogeneous subgroups, called strata, and then applying Simple Random Sampling within each subgroup.

As a result, the test set is representative of the population, since the percentage of each stratum is preserved. The strata should be disjointed; therefore, every element within the population must belong to one and only one stratum.

Now let’s consider a real example. The Italian population is 48.7 males and 51.3 females, so a survey in Italy should be done by picking a sample of individuals while maintaining this ratio. If the survey sample contains 1000 individuals, then the Stratified Sampling picks exactly 487 males and 513 females. If Simple Random Sampling is performed, then the right percentage of males and females isn’t preserved, and the survey results will be significantly biased.

3. Steps Involved in Stratified Sampling

We can easily implement Stratified Sampling by following these steps:

• Set the sample size: we define the number of instances of the sample. Generally, the size of a test set is 20% of the original dataset, but it can be less if the dataset is very large.
• Partitioning the dataset into strata: in this step, the population is divided into homogeneous subgroups based on similar features. Each instance of the population must belong to one and only one stratum.
• Apply Simple Random Sampling for each stratum: random samples are taken from each stratum with the same proportion defined in the first step.

Here, we’ll represent the procedure schematically:

4. Advantages and Limitations

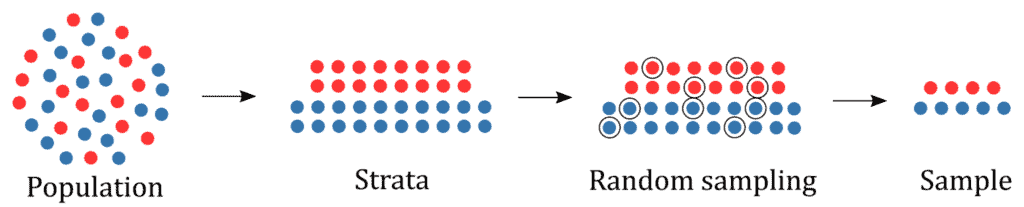
Stratified Sampling ensures each group within the population receives the proper representation within the sample. When the population can be partitioned into homogeneous subgroups, this technique gives a more accurate estimate of model parameters than random sampling.

However, simple random sampling is more advantageous when the population can’t be divided into subgroups, since there are too many differences within the population.

5. Example

Now let’s consider an example of a binary classifier that predicts if a digit is nine or not. We’ll perform the K-Fold Cross Validation with the Stratified Sampling in order to assess the performance of the classifier. Then we’ll exploit the StratifiedKFold class provided in the Python package Scikit-Learn.

We’ll make our analysis with the training set of the MNIST dataset that we’ll normalize in the range :

import numpy as np
from keras.datasets import mnist

(x, y), (_, _) = mnist.load_data()
x = x.reshape(-1, 28*28) / 255.0

Then we’ll create a target vector for this binary classification task:

y = (y == 9) 

Note that this dataset is imbalanced since the negative instances (not-9) are more frequent than the positive ones (9).

Now let’s train and test a Stochastic Gradient Descent (SGD) classifier with the Stratified K-Fold Cross Validation using Scikit-Learn:

from sklearn.linear_model import SGDClassifier
from sklearn.model_selection import StratifiedKFold

skfolds = StratifiedKFold(n_splits=3)
splits = skfolds.split(x, y)
for i, (train_index, test_index) in enumerate(splits):  
  x_train = x[train_index]
  y_train = y[train_index]
  x_test  = x[test_index]
  y_test  = y[test_index]
  clf = SGDClassifier()
  clf.fit(x_train, y_train)
  y_pred = clf.predict(x_test)
  accuracy = np.mean(y_pred == y_test)
  print("[SPLIT %d]"%(i+1))
  print("Percentage of digit 9 in the original dataset: %.2f %%"%(np.mean(y==True)*100))
  print("Percentage of digit 9 in the training set: %.2f %%"%(np.mean(y_train==True)*100))
  print("Percentage of digit 9 in the test set: %.2f %%"%(np.mean(y_test==True)*100))
  print("Accuracy: %.4f"%accuracy) 

At each iteration, the code splits the dataset using the stratified sampling, trains the classifier on the training folds, makes inference on the test fold, and evaluates the overall accuracy. Finally, it prints out the percentage of instances belonging to the positive class in the original dataset, the training set, and the test set at each iteration.

The percentage of the positive class is preserved for each split as expected:

Now let’s consider the K-Fold Cross Validation without Stratified Sampling. We must replace StratifiedKFold with the KFold class in the above code:

from sklearn.model_selection import KFold
skfolds = KFold(n_splits=3)

Now we’ll get the following output:

We can see that the proportion of the percentage of the positive class varies hugely among the original dataset, training set, and test set within each split because we haven’t used the Stratified Sampling.

6. Conclusion

In this article, we examined Stratified Sampling, a sampling technique used in Machine Learning to generate test sets. We also discussed the advantages and limitations of the technique. Finally, we learned how to apply the K-Fold Cross Validation with Stratified Sampling to evaluate a digit classifier using a Python implementation.