Learn through the super-clean Baeldung Pro experience:
>> Membership and Baeldung Pro.
No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.
Last updated: March 18, 2024
In this tutorial, we explore maximum likelihood estimation through an example. We take care to introduce likelihood as distinct from probability. We go on to show what estimating the maximum likelihood of a dataset means. Then, we discuss how it can be used as the basis for optimizing many types of models.
Maximum likelihood is a method used in statistics, and machine learning, to estimate the parameters of a model. It involves finding the parameter values that maximize the likelihood of the data given in the model. This means that the parameter values that we find using maximum likelihood are those that make the observed data most probable, given the model.
In other words, the maximum likelihood estimate of a parameter is the value that is most likely to have produced the observed data, assuming that the model is correct. This method estimates the parameters of various statistical models, including regression models, logistic models, and many others.
It is helpful here to clarify the difference between likelihood and probability. Probability tells us the chance that some piece of data was observed given a model. The likelihood, by contrast, tells us the chance some model generated the given data. Here we use the term chance loosely to convey the intuition, and further, we show the corresponding formula.
Probability is a function of the observations parameterized by the function’s parameters. If this model describes the data, how probable is a specific example:
(1)
The likelihood is a function of the parameters of the chosen distribution, parameterized by the observations:
(2)
Finally, this quote helps to solidify the important takeaways. The distinction between probability and likelihood is fundamentally important: Probability attaches to possible results; likelihood attaches to hypotheses. From this, we also infer that Likelihood is not a probability density function. This is because the sum over hypotheses does not have to sum to 1.
Now that we have an intuition for probability and likelihood, we start putting the concepts together. Since the likelihood is the probability a specific parameterization leads to observing the data, we can equate our two formulas:
(3)
Now, maximizing the Likelihood is equivalent to maximizing the probability of the samples in our dataset.
We’ll now walk through the steps to create an optimization problem. First, let’s rewrite the equation above.
For a probability density function that turns into a product of the terms. In the case of a discrete problem, we have a probability mass function. In that case, instead of a product, the probability mass function is represented as a sum instead:
(4)
In reality, it is often easier to maximize the log of the above equation. Alternatively, we can minimize the negative log-likelihood. This is a common approach in machine learning. In either case, we take the log of the probability density function:
(5)
We then bring the log inside the product and, consequently, convert it to a sum.
(6)
This produces a value that we can now apply an optimization algorithm to. That could be a population-based heuristic optimization method such as moth-flame optimization or ant-lion optimization. It could also be a hill climbing or related method such as simulated annealing.
By inverting the sign and making the result negative, we can also create a minimization problem where we minimize the negative log-likelihood. This is standard and would allow us to apply SciPy’s minimize function or even neural networks to solve the problem.
It is also worth noting that maximum likelihood estimation is related to other optimization techniques. In particular, if we assume a normal distribution, then it is equivalent to the ordinary least squares method.
The ordinary least squares method is a consistent estimator. This means that as more data becomes available, it converges closer to the true data distribution. Through the equivalence between ordinary least squares and maximum likelihood estimation, we can also say that maximum likelihood is a consistent estimator.
For example, we want to represent the distribution of mouse weights from a given dataset containing the measured weight of a set of mice. The weights of the mice are shown in the plot. Maximum likelihood estimation is a method of optimizing the parameters of a model. In order to use it, we need to choose a model:
Looking at the plot of mouse weights, we could say our data looks normally distributed. The data seems to appear bunched together towards the middle and then becomes less dense towards the edges. Many real-life examples fit this distribution.
We define the Gaussian (normal) distribution by two parameters. The mean and the variance
. We use maximum likelihood to fit these two parameters of our distribution/model.
If the model is properly fit, we will have a parameterized distribution that, if we sample from it, is the distribution that is most likely to produce the initially observed samples.
We see three examples of differently parameterized Gaussian distributions in the graph below. We use the maximum likelihood estimate to choose which is best. An optimization method is used if better results are required. This allows us to find even better parameters for the distribution:
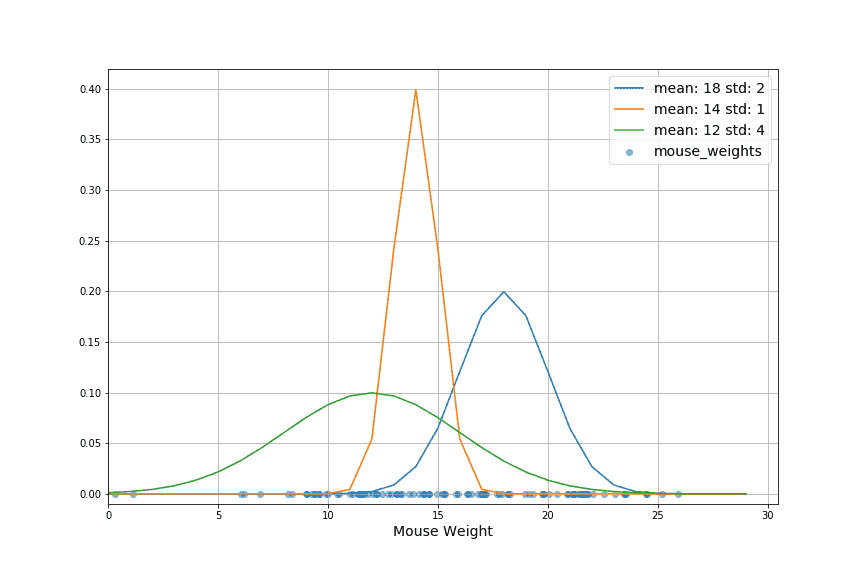
In this case, the mean and standard deviation of the data produce the best-fitting Gaussian. The method generalizes beyond the Gaussian distribution to other distributions and models.
We use maximum likelihood estimation in a wide variety of applications, including the following:
Estimating the parameters of statistical models: We use maximum likelihood to estimate the parameters of many different types of statistical models, including models for both regression and classification tasks. Negative log-likelihood, the inverted version for minimization, is useful when optimizing neural networks.
Inferring population parameters from sample data: We use maximum likelihood to estimate population parameters (such as the mean and variance of a distribution) from sample data. This is useful as a tool for data analysis.
Model selection: We also use maximum likelihood to compare the fit of different models to the data and choose the best-fitting model based on the maximum likelihood estimate of the parameters.
As is the case for all estimation methods, there are several limitations to consider when using maximum likelihood estimation.
The user must specify the model correctly: In maximum likelihood estimation, we assume a model that fits the data. That means that we choose the model we use to describe the data. If the model is misspecified, the maximum likelihood estimate of the parameters may be biased or inconsistent.
In our examples, the equations that allow us to select the parameters that optimize our chosen model need to be explicitly worked out.
In this tutorial, we introduced maximum likelihood estimation. We highlighted the difference between likelihood and probability. We went on to describe how the concepts can be related in order to create an optimization problem.
With this understanding, we discussed how to use maximum likelihood estimation to solve an optimization problem, select a model and inspect population parameters. This description highlighted the ubiquity of maximum likelihood estimation across statistics and machine learning applications.
Modeling data through its statistical properties is a fundamental aspect of many artificial intelligence applications. An understanding of maximum likelihood is key to developing a deeper understanding of many applications, why they work, and what their limitations are.