1. Introduction
In this tutorial, we’ll show how to root a tree.
2. Tree, Graphs, and Roots
Typically, trees are stored as hierarchical structures with one node serving as the root:
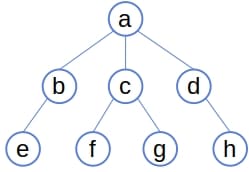
The root acts as the entry point through which we can reach all other nodes by following parent-child edges.
However, trees can sometimes be stored as graphs, meaning they lack a root but instead have an adjacency list or matrix.
Our goal is then to convert such a graph into a tree.
3. Rooting a Tree
To make node the root, we use depth-first search (DFS) to visit all the nodes starting from
:
The stack contains the candidate leaves of the tree. These nodes are the ones whose children we know nothing about yet. In each iteration, we check the deepest candidate to determine if it has any children. If it does, we add them to the stack. Otherwise, we confirm the node as a leaf. In either case, we remove the node from the stack because it’s no longer a candidate.
Once we traverse all the vertices, we’ll have a tree spanning the entire input.
3.1. Example
Let’s root the following graph at node 5:
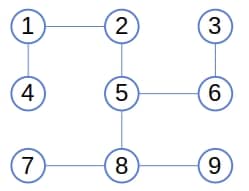
At first, the stack contains only the root, node 5. Then, we get its children, nodes 2, 6, and 8, add them to the tree, and push them onto the stack. Afterward, we pop node 2, visit its child, add it to the tree, and push it onto the stack. Continuing this process, we get the following:
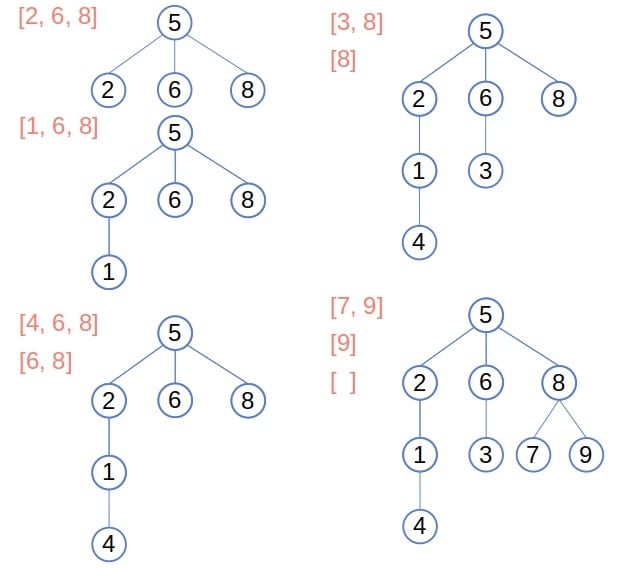
The algorithm stops when the stack becomes empty.
3.2. Complexity
Let be the maximal number of children a node can have and
the total number of nodes. The time and space complexity depend on the way the nodes are stored initially.
If we use the adjacency lists, we’ll traverse each edge twice and visit each node at most times. That’s because the
function iterates only over the nodes of the given node. If
is constant with respect to
, the time complexity is
since a tree with
nodes has
edges. The space complexity will also be
.
However, if we use the adjacency matrix, we’ll take memory to store the nodes. The
function will then traverse all the
bits in the corresponding row to find the neighbors of
. So, the time complexity will also be
.
4. Issues
Our algorithm assumes the root is already chosen. It’s often a good idea to choose the center of the tree as its root, as that minimizes the resulting tree’s height.
DFS is effective only if the input nodes form a tree. If there are cycles, DFS gets stuck in a loop. To avoid that, we can mark each node the first time we add it to the tree.
Another issue is that the nodes might be disconnected. In this case, will span only the nodes in the same component as the chosen root node.
5. Conclusion
In this article, we showed how to root a tree using the depth-first traversal with a time complexity of . However, if the input nodes don’t form a tree, this approach won’t work without modifications.