Connected Components in a Graph | Baeldung on Computer Science

1. Overview

In this tutorial, we’ll discuss the concept of connected components in an undirected graph.

We’ll go through some simple examples to get a basic understanding, and then we’ll list out the properties of connected components.

2. Connected Component Definition

A connected component or simply component of an undirected graph is a subgraph in which each pair of nodes is connected with each other via a path.

Let’s try to simplify it further, though. A set of nodes forms a connected component in an undirected graph if any node from the set of nodes can reach any other node by traversing edges. The main point here is reachability.

In connected components, all the nodes are always reachable from each other.

3. Few Examples

In this section, we’ll discuss a couple of simple examples. We’ll try to relate the examples with the definition given above.

3.1. One Connected Component

In this example, the given undirected graph has one connected component:

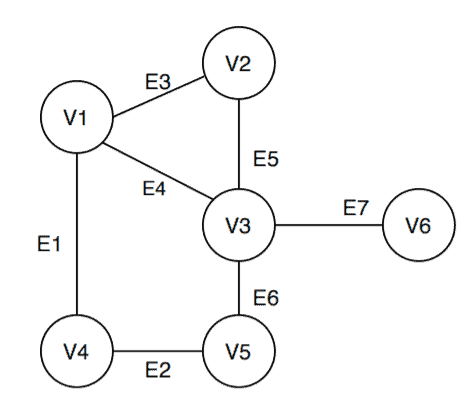
Let’s name this graph $G1(V, E)$ . Here $V = \{V1, V2, V3, V4, V5, V6\}$ denotes the vertex set and $E = \{E1, E2, E3, E4, E5, E6, E7\}$ denotes the edge set of $G1$ . The graph $G1$ has one connected component, let’s name it $C1$ , which contains all the vertices of $G1$ . Now let’s check whether the set $C1$ holds to the definition or not.

According to the definition, the vertices in the set $C1$ should reach one another via a path. We’re choosing two random vertices $V1$ and $V6$ :

$V6$ is reachable to $V1$ via: $E4 \rightarrow E7 \ or\ E3 \rightarrow E5 \rightarrow E7 \ or\ E1 \rightarrow E2 \rightarrow E6 \rightarrow E7$
$V1$ is reachable to $V6$ via: $E7 \rightarrow E4 \ or\ E7 \rightarrow E5 \rightarrow E3 \ or\ E7 \rightarrow E6\rightarrow E2 \rightarrow E1$

The vertices $V1$ and $V6$ satisfied the definition, and we could do the same with other vertex pairs in $C1$ as well.

3.2. More Than One Connected Component

In this example, the undirected graph has three connected components:

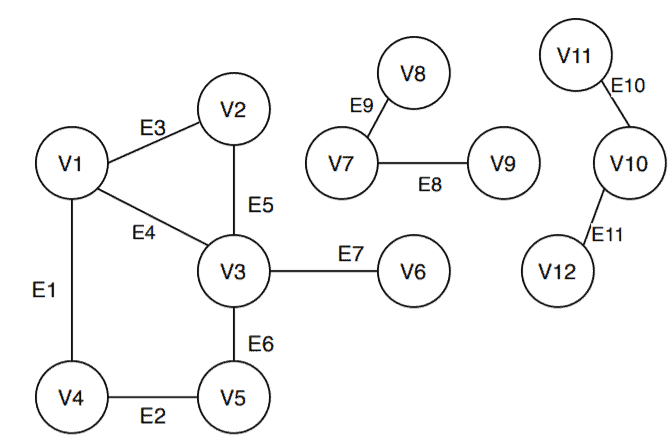
Let’s name this graph as $G2(V, E)$ , where $V = \{V1, V2, V3, V4, V5, V6, V7, V8, V9, V10, V11, V12\}$ , and $E = \{E1, E2, E3, E4, E5, E6, E7, E8, E9, E10, E11\}$ . The graph $G2$ has 3 connected components: $C1 = \{V1, V2, V3, V4, V5, V6\}$ , $C2 = \{V7, V8, V9\}$ and $C3 = \{V10, V11, V12\}$ .

Now, let’s see whether connected components $C1$ , $C2$ , and $C3$ satisfy the definition or not. We’ll randomly pick a pair from each $C1$ , $C2$ , and $C3$ set.

From the set $C1$ , let’s pick the vertices $V4$ and $V6$ .

$V6$ is reachable to $V4$ via: $E2 \rightarrow E6 \rightarrow E7 \ or\ E1 \rightarrow E4 \rightarrow E7 \ or\ E1 \rightarrow E3 \rightarrow E5 \rightarrow E7$
$V4$ is reachable to $V6$ via: $E7 \rightarrow E6 \rightarrow E2 \ or\ E7 \rightarrow E4 \rightarrow E1 \ or\ E7 \rightarrow E5 \rightarrow E3 \rightarrow E1$

Now let’s pick the vertices $V8$ and $V9$ from the set $C2$ .

$V9$ is reachable to $V8$ : $E9 \rightarrow E8$
$V8$ is reachable to $V9$ : $E8 \rightarrow E9$

Finally, let’s pick the vertices $V11$ and $V12$ from the set $C3$ .

$V11$ is reachable to $V12$ : $E11 \rightarrow E10$
$V12$ is reachable to $V11$ : $E10 \rightarrow E11$

So from these simple demonstrations, it is clear that $C1$ , $C2$ , and $C3$ follow the connected component definition.

4. Properties

As we have already discussed the definition and demonstrated a couple of examples of the connected components, it’s a good time to list out some of the important properties that connected component always holds.

First of all, the connected component set is always non-empty.

Moreover, if there is more than one connected component for a given graph then the union of connected components will give the set of all vertices of the given graph.

For example $G2$ :

$C1 \,\cup \,C2 \,\cup \,C3 = \{V1, V2, V3, V4, V5, V6\} \,\cup \,\{V7, V8, V9\} \,\cup\, \{V10, V11, V12\} = \{V1, V2, V3, V4, V5, V6, V7, V8, V9, V10, V11, V12\} = V$

Finally, connected component sets are pairwise disjoint. That means if we take the intersection between two different connected component sets then the intersection will be equals to an empty set or a null set.

Let’s consider the connected components of graph $G2$ again. In $G2$ , let’s check this property:

$C1 \,\cap\, C2 \,\cap\, C3 = \{V1, V2, V3, V4, V5, V6\} \,\cap\, \{V7, V8, V9\} \,\cap\, \{V10, V11, V12\} =\{\varnothing\}$

5. Finding Connected Components

Given an undirected graph, it’s important to find out the number of connected components to analyze the structure of the graph – it has many real-life applications. We can use either DFS or BFS for this task.

In this section, we’ll discuss a DFS-based algorithm that gives us the number of connected components for a given undirected graph:

algorithm FindConnectedComponents(G):
    // INPUT
    //    G = an undirected graph with vertices V and edges E
    // OUTPUT
    //    The number of connected components in G

    Component_Count <- 0
    Visited <- an empty map from vertices to boolean values 

    for vertex k in V:
        Visited[k] <- false

    for ertex k in V:
        if not Visited[k]:
            DFS(V, k)
            Component_Count <- Component_Count + 1

    print Component_Count

algorithm DFS(V, k):
    // INPUT
    //    V = the set of vertices in the graph
    //    k = the current vertex being explored
    // OUTPUT
    //    Executes a depth-first search starting from vertex k,
    //    marking all reachable vertices as visited.

    Visited[k] <- true
    for vertex p in Adj[k]: // Adj[k] is the adjacency list of k
        if not Visited[p]:
            DFS(V, p)

The variable Component_Count returns the number of connected components in the given graph.

We start by initializing all the vertices to the flag not visited. We then choose any random vertex to start and check if we’ve visited the vertex or not. If we didn’t, we call the DFS function.

Once all the vertices marked as visited, the algorithm terminates and prints the number of the connected components.

In the DFS function, the arguments that we pass are a vertex set containing all the vertices of the given graph and a particular vertex that must belong to the vertex set.

First, we mark the particular input vertex as visited. Then we calculate the adjacent vertices of the given particular input vertex. For each adjacent vertex, we check whether we visited them or not. If not, then we call the DFS function recursively until we mark all the adjacent vertices as visited.

The key point to observe in the algorithm is that the number of connected components is equal to the number of independent DFS function calls. The Component_Count variable counts the number of calls. Of course, this doesn’t include the calls that are being made under the DFS() function recursively.

6. Test Run

Let’s run the algorithm on a sample graph:

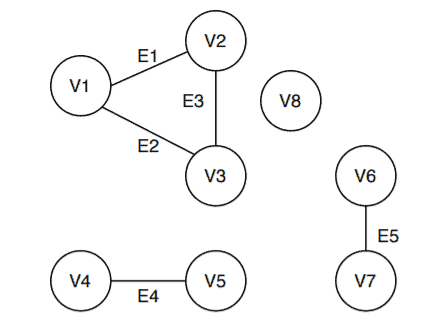
Given an undirected graph $G3(V, E)$ , where $V = \{V1, V2, V3, V4, V5, V6, V7, V8\}$ , and $E = \{E1, E2, E3, E4, E5\}$ .

The first step of the algorithm is to initialize all the vertices and mark them as not visited.

The red vertex denotes that it is not visited. The green vertex denotes it is visited by the algorithm:

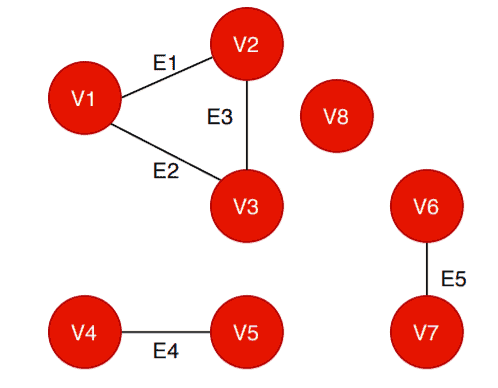
We can pick any vertex from the vertex list to start the algorithm. Let’s pick $V1$ .

The algorithm checks whether it is visited or not. In this case, $V1$ is not visited. So it calls $DFS(V, V1)$ .

Within the DFS(), first, it labels the vertex $V1$ as visited and searches for the adjacent vertices of $V1$ . All the adjacent vertices are also marked as visited. When DFS finishes visiting all the adjacent vertices of $V1$ , the Component_Count becomes 1, and the status of vertices are updated:

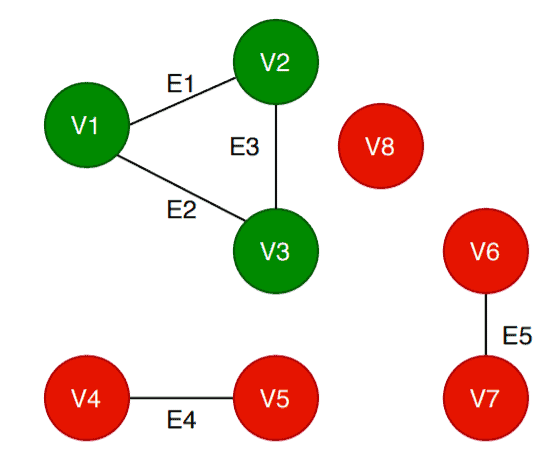
Again, the algorithm picks any random vertex. Let’s pick $V4$ this time.

It checks whether $V4$ is already visited or not. As it is not visited so the algorithm calls $DFS(V, V4)$ . Again the algorithm marks the vertex $V4$ mark as visited, and DFS searches for its adjacent vertices and marks them as visited. Now the Component_Count becomes 2, and the status of the vertex list is updated again:

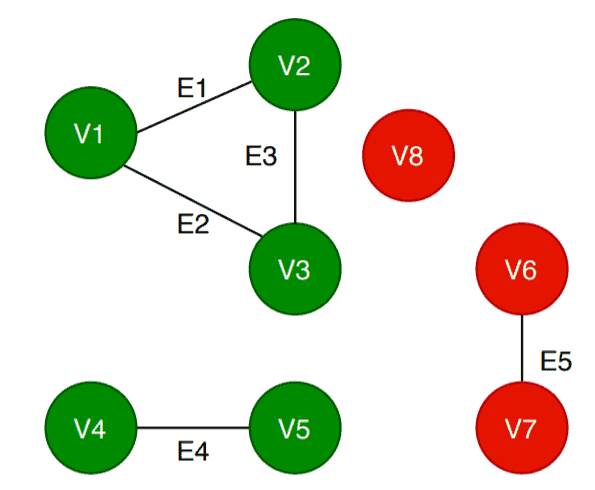
The algorithm continues and chooses $V6$ , checks the status, and calls $DFS(V, V6)$ . The vertex $V6$ and its adjacent vertices are labeled as visited and the Component_Count increases to 3. The algorithm updates the vertex list status:

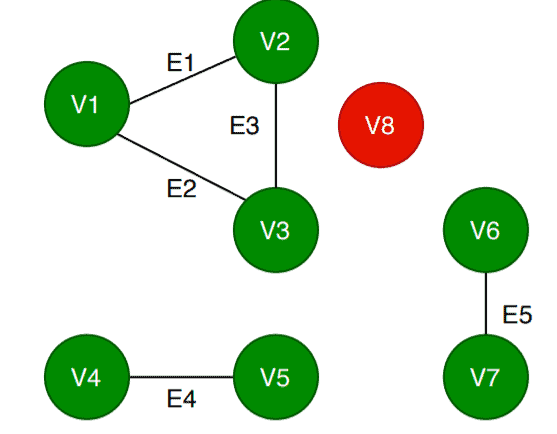
Finally, the algorithm chooses $V8$ , calls $DFS(V, V8)$ , and makes $V8$ as visited. The vertex $V8$ doesn’t have any adjacent vertices so DFS returns and Component_Count increases to 4. Finally, the algorithm updates the status of the vertex list:

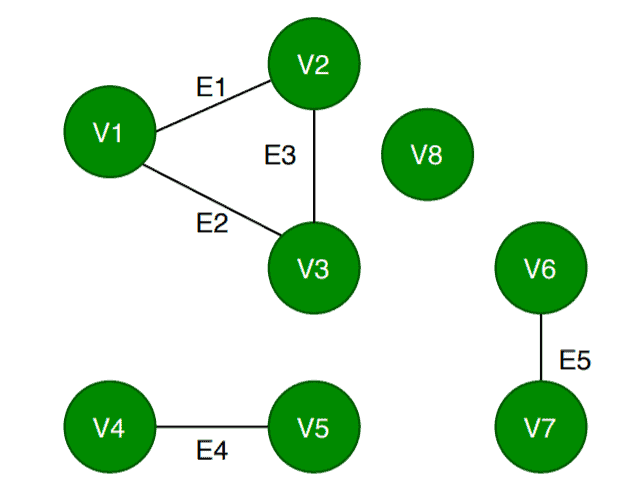
As the algorithm finished traversing all the vertices of the graph $G3$ , it terminates and returns the value of Component_Count which equals the number of connected components in $G3$ . In this case, the algorithms find four connected components in $G3$ :

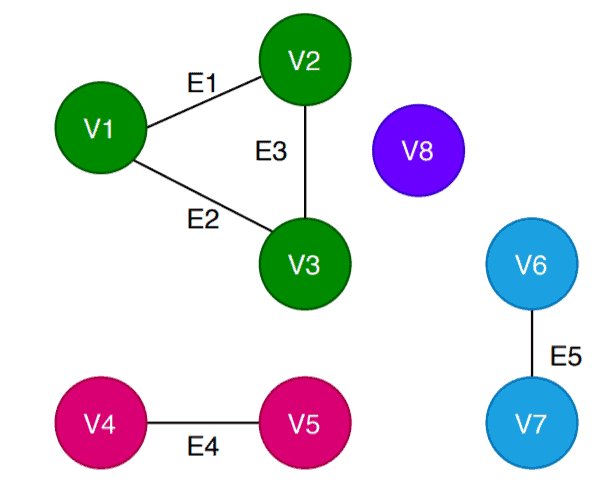
We used four different colours to illustrate the connected components in $G3$ , namely: $C1 = \{V1, V2, V3\}$ , $C2 = \{V4, V5\}$ , $C3 = \{V6, V7\}$ , $C4 = \{V8\}$ .

7. Time Complexity Analysis

The algorithm we just saw for finding connected components in a given undirected graph uses the DFS search and counts the number of calls to the DFS function. If the graph is represented by the adjacency list, then the DFS search visits all the vertices once and each edge twice in case of an undirected graph. The checking of the vertex status takes $O(1)$ time. Thus in total, our algorithm will take $\mathbf{O(V+E)}$ time.

In case the graph is represented by the adjacency matrix, the DFS search takes $O(V^2)$ time as it needs to traverse the entire row to evaluate the neighbor vertices. The checking of the vertex status again takes $O(1)$ time. Thus giving us a total of $\mathbf{O(V^2)}$ time.

8. Conclusion

In this article, we discussed a simple definition of connected component followed by a couple of simple and easy to understand examples. Also, we listed out some common but important properties of connected components.

Then, we discussed a DFS search-based algorithm to find the number of connected components in a given graph. We demonstrated the algorithm with the help of a sample graph. Lastly, we analyzed the time complexity of the algorithm.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex