Cycles in an Undirected Graph

1. Overview

In this tutorial, we’re going to learn to detect cycles in an undirected graph using Depth-First Search (DFS).

2. What Is a Graph?

A graph is a data structure that comprises a restricted set of vertices (or nodes) and a set of edges that connect these vertices.

We can define a graph , with a set of vertices , and a set of edges . Every edge connects two vertices, and we can show it as , where and are connected vertices.

For example, if there is an edge between two vertices  and , then we call them associated. We can then also call these two as adjacent (neighbor) vertices.

Mathematically, we can show a graph ( vertices, edges) as:

We can categorize graphs into two groups:

First, if edges can only be traversed in one direction, we call the graph directed.

For example, if a directed edge connects vertex 1 and 2, we can traverse from vertex 1 to vertex 2, but the opposite direction (from 2 to 1) is not allowed. So, we can say that is not equal to .

But, if the edges are bidirectional, we call the graph undirected.

For example, if an undirected edge connects vertex 1 and 2, we can traverse from vertex 1 to vertex 2 and from 2 to 1. We can then say that is equal to .

3. What Is a Cycle?

In graph theory, a path that starts from a given vertex and ends at the same vertex is called a cycle.

Cycle detection is a major area of research in computer science. The complexity of detecting a cycle in an undirected graph is .

In the example below, we can see that nodes 3-4-5-6-3 result in a cycle:

4. Cycle Detection

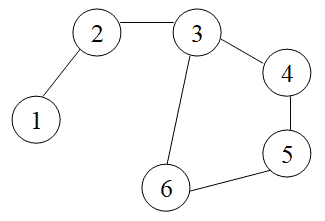
Next, then, let’s learn how to detect cycles in an undirected graph. Specifically, let’s use DFS to do it.

As a quick reminder, DFS places vertices into a stack. We start with some vertex and push it onto the stack. Then:

1. If has unvisited neighbors, we push one of those neighbors, , onto the stack and repeat this step (now is )
2. Once has no unvisited neighbors, we pop it off of the stack and return to step 1

Now, to detect a cycle, we can adjust DFS’s logic a bit: If has a visited neighbor that:

• is equal to , or
• is not equal to ‘s parent

then we’ve got a cycle.

Putting this into pseudocode, we get:

algorithm detectcycle(v_n):
    // INPUT
    //   v_n = current vertex in G
    // OUTPUT
    //   true if a cycle is found; otherwise, returns false
    mark(v_n, visited)
    for u_n in neighbors(v_n):
        if mark(u_n) = visited:
            if v_n = u_n or u_n != parent(v_n):
                return true
        else if detectcycle(u_n):
            return true
    return false

And now we can use it to detect cycles in undirected graphs by calling .

5. Conclusion

In this quick tutorial, we explored how to detect cycles in undirected graphs – basing our algorithm on Depth-First Search.