Learn through the super-clean Baeldung Pro experience:
>> Membership and Baeldung Pro.
No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.
Last updated: March 18, 2024
In this tutorial, we’ll discuss multiobjective algorithms and Pareto frontiers with examples. We’ll present the general steps in a multiobjective algorithm and explain the importance of the Pareto frontier.
Finally, we’ll explore some advantages and disadvantages of multiobjective algorithms.
Multiobjective algorithms are optimization techniques used to find optimal solutions with respect to multiple objectives or goals. We can use these algorithms to solve problems across various fields, including engineering, robotics, design, and public policy.
We utilize multiobjective algorithms to solve multi-faceted problems that require trade-offs and prioritization. Additionally, these algorithms are particularly useful for solving complex problems with no single best solution but rather a set of solutions based on different objectives.
Let’s discuss an example. A company wants to find the optimal production level for multiple products while minimizing costs and maximizing profits. Therefore, the decision variables include the production levels of each product. Additionally, the objective function consists of the total cost and total profit.
Furthermore, the constraints include production capacity and market demand for each product. The solution to this problem would be a set of production levels that balances the trade-off between minimizing costs and maximizing profits.
Some examples of multiobjective algorithms are evolutionary algorithms, genetic algorithms, particle swarm optimization, tabu search, and simulated annealing.
A Pareto frontier is a graph that plots the best solutions for each objective. The name Pareto is derived from the 80-20 principle, which states that 80% of the outcomes come from 20% of the causes. A Pareto graph returns the best solutions for a given problem. It also provides insights into how the solutions are distributed among all the objectives.
In a multiobjective optimization problem, there may be multiple solutions that are considered optimal, as each solution may optimize one objective function at the expense of the others. The Pareto frontier is a set of solutions that represents the best trade-off between all the objective functions. A solution not dominated by any other solution in the feasible solution space is considered to be on the Pareto frontier.
Generally, we plot the Pareto frontier solution on a two-dimensional graph, with one axis representing an objective and the other representing the best solution for that objective. It can help illustrate the trade-offs between different objectives.
Let’s talk about an example. A company produces multiple products and wants to find the best design for each product. The company aims to minimize the cost of production and maximize the product’s performance.
The decision variables in this problem would be the design characteristics of each product, such as materials and manufacturing processes. The objective functions include the total cost of production and the performance of each product. The constraints contain manufacturing capabilities and market demand for each product.
The Pareto frontier for this problem would be a set of product designs representing the best trade-off between minimizing production costs and maximizing performance. A design on the Pareto frontier would be one that can’t be improved in terms of performance without increasing the cost of production and vice versa.
Now let’s talk about the general steps in a multiobjective algorithm:
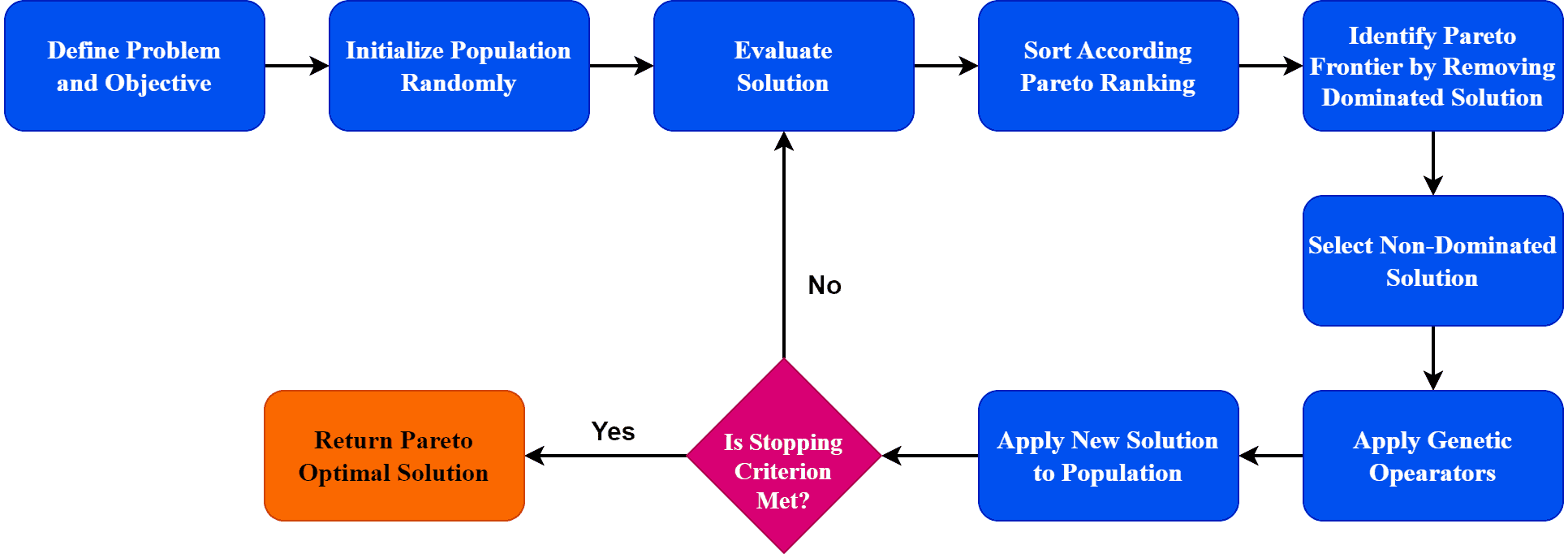
The first step is to define the problem and objectives. This step defines the problem as a set of decision variables and constraints. Additionally, we define the objectives. Furthermore, the objectives should be quantifiable so that we can evaluate the performance of the solutions.
The second step is to initialize the population randomly. In this step, we generate a random population. Additionally, the population’s size depends on the problem’s complexity. The next step is to evaluate the generated solutions. We evaluate the solutions according to the objectives. It’s an important step as it allows the algorithm to rank the solutions based on their performance. The evaluation process can be computationally expensive. Therefore, it’s crucial to choose efficient evaluation methods.
In order to identify the optimal solution, we sort the solutions according to the Pareto ranking. A Pareto ranking compares the solutions based on their performance on each objective. We call a solution Pareto-optimal if any other solution in the feasible solution space doesn’t dominates it. In other words, it’s a solution that we can’t improve in one or more objectives without worsening other objectives.
Based on the Pareto ranking, we identify the Pareto frontier solutions. Additionally, we identify the Pareto frontier solutions by removing dominated solutions. Furthermore, the remaining solutions form the Pareto frontier, representing the set of non-dominated solutions considered the best trade-off solutions. The next step is to select the non-dominated solutions for reproduction. In order to implement the reproduction step and generate new solutions, we apply genetic operators such as crossover and mutation.
Finally, we add new solutions to the population. At this point, we check if the solution we generated met the stopping condition. If it satisfies the stopping requirement, we return the Pareto optimal solution. Otherwise, we go back to the evolution of the randomly generated solution step and start with a new set of solutions. Furthermore, we repeat this step until the stopping criterion is met.
Multiobjective algorithms have several advantages over traditional optimization methods. They’re best suited to situations where we must prioritize different objectives.
Multiobjective algorithms can help us understand how changes to one objective affect other objectives. Additionally, we can find the set of Pareto optimal solutions representing the best trade-off between all objectives. This allows decision-makers to choose the solution that best fits their needs. Furthermore, they can be applied to many areas and assist in decision-making across many fields. They’re applicable in engineering, robotics, design, public policy, and many other fields.
These algorithms can handle large-scale, complex problems with a large number of decision variables and objectives. Additionally, multiobjective algorithms are robust to noise in the objective functions, making them more reliable for real-world problems.
Multiobjective optimization algorithms can provide a better decision-making process by providing a set of alternatives for the decision-maker to choose from instead of a single solution.
Now let’s talk about the disadvantages. Multiobjective algorithms are typically more complex than traditional algorithms, making them difficult to implement and understand. Additionally, these algorithms often require making trade-offs between different objectives. In practice, trade-offs between different objectives are challenging to perform.
Due to the high computational expense, multiobjective algorithms suffer from scalability issues. Finally, it’s hard to visualize the solutions to multiobjective problems.
In this tutorial, we discussed multiobjective algorithms and Pareto frontiers with examples. We explored the general steps in a multiobjective algorithm and the importance of the Pareto frontier. Finally, we presented some advantages and disadvantages of multiobjective algorithms.