Genetic Algorithms: Crossover Probability and Mutation Probability

Let’s look at the steps involved in a genetic algorithm:

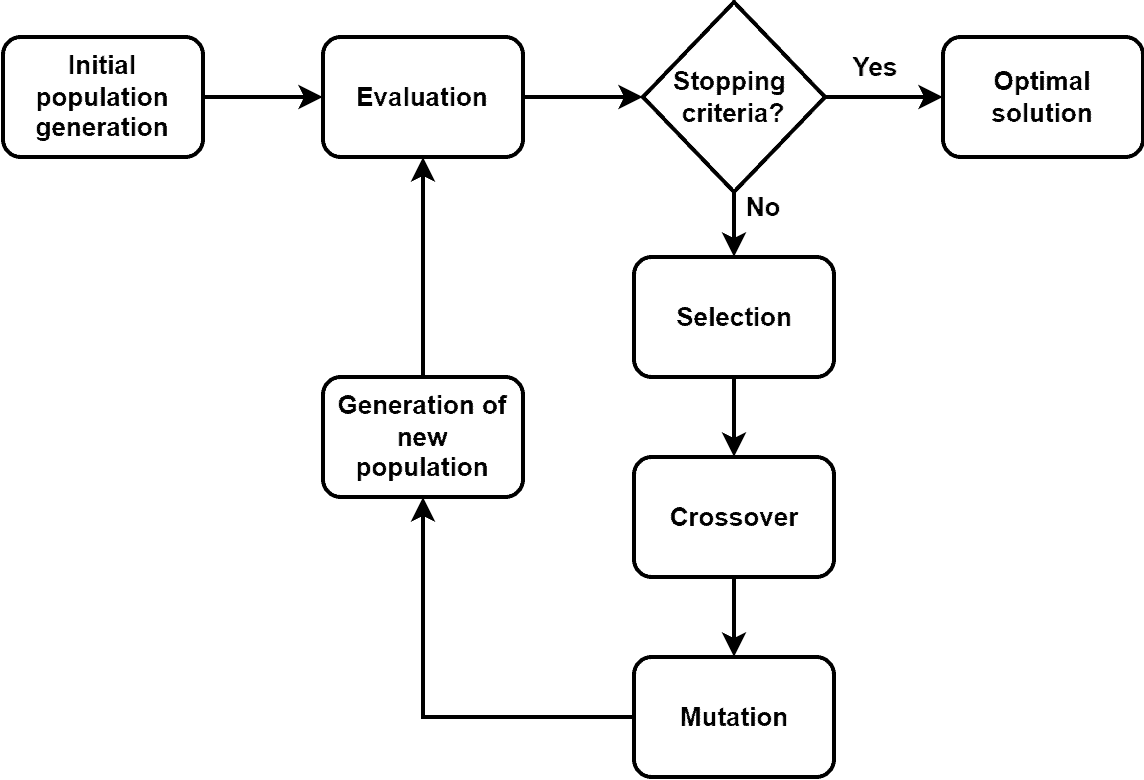
The first step of a genetic algorithm is initialization. In this step, the initial population of solutions, known as chromosomes, is generated randomly. The size of the population and the representation of the chromosomes depend on the given problem.

The next step is to evaluate the initial population. In this step, we evaluate each chromosome in the population using a fitness function, which measures how well the chromosome solves the problem. The fitness function is typically defined based on the problem being solved and the desired characteristics of a good solution.

After the evaluation step, we terminate the algorithm if we can find our desired solution. If we can’t find the desired solution, we go to the next step. In this step, we identify the fittest chromosomes to generate the new population of solutions.

As soon as we identify the fittest chromosomes, we combine them to produce new offspring. Crossover, also known as recombination, involves taking pieces of two or more parent chromosomes. Furthermore, we combine them to create one or more offspring chromosomes.

Finally, we introduce random changes or mutations into the offspring chromosomes. Mutation helps to introduce new genetic diversity into the population and can help to prevent the algorithm from getting stuck in a local minimum.

3. Crossover Probability

Crossover events are an essential mechanism for generating genetic diversity. It also plays a crucial role in the evolution of species. In a genetic algorithm, the crossover generates a new solution from two existing solutions. We also call the existing solutions as parents in genetic algorithms. The crossover probability is a parameter that controls the likelihood that crossover will occur between two parent solutions.

If we set the crossover probability to a high value, it’s more likely that crossover will occur between a pair of parents. Hence, it results in new solutions that combine the best features of both parents. If we set the crossover probability to a low value, it’s less likely that crossover will occur. Additionally, the new solutions will be more similar to the parents.

The optimal value for the crossover probability depends on the specific problem and the characteristics of the population. In general, a higher crossover probability can lead to a faster convergence on a solution. However, it can also result in a loss of diversity in the population. Loss of diversity can be detrimental to the performance of the genetic algorithm.

Crossover probability is often used in genetic research to study the inheritance of traits and the structure of the genome. It can also predict the likelihood of specific genetic combinations occurring in offspring. Understanding crossover probability can help researchers better to understand the genetic basis of traits and diseases. Additionally, it helps to develop new strategies for diagnosing and treating genetic conditions.

4. Mutation Probability

In a genetic algorithm, the mutation is a genetic operation that introduces new genetic material in a population. We utilize this technique to maintain genetic diversity from one generation of the population to another. Additionally, we use it to prevent the genetic algorithm from getting stuck in a local minimum or convergence on a suboptimal solution.

Mutation probability is a parameter in a genetic algorithm that determines the likelihood that an individual will undergo the mutation process. We usually set it to a low value, such as 0.01 or 0.001. The low value ensures only a tiny fraction of the population is mutated at each generation. A higher value of mutation probability encourages the exploration of the search space. However, it can also increase the chances of the genetic algorithm getting stuck in a suboptimal solution.

Understanding mutation probability can help researchers to understand the genetic basis of traits and diseases. Additionally,  it can play a vital role in developing new strategies for diagnosing and treating genetic diseases.

5. Trade-Offs

Crossover and mutation probabilities control the rate of change of chromosomes in a population. We use both techniques to generate a new population from the initial population. Therefore, they play a crucial role when it comes to improving the performance of a genetic algorithm. By increasing crossover and mutation probabilities, we can change the population.

Let’s talk about the trade-off between crossover and mutation probabilities. A higher mutation probability can lead to more search space exploration. However, it can also increase the chances of the genetic algorithm getting stuck in a suboptimal solution.

On the other hand, a higher crossover probability can lead to more exploitation of good solutions. Although, it can also reduce the diversity of the population and increase the chances of convergence on a suboptimal solution.

In general, finding a balance between mutation and crossover is essential. The balance ensures the genetic algorithm can explore the search space effectively while preserving good solutions. Additionally, we can avoid convergence on suboptimal solutions.

Several factors, such as the population’s size, the problem’s structure, and the genetic algorithm’s specific goals, influence the balance between crossover and mutation probabilities.

6. Optimal Values for Crossover and Mutation

The optimal values for crossover and mutation probabilities depend on the problem’s specific goals and constraints. When choosing values for crossover and mutation probabilities, it can be helpful to consider the following factors:

• Size and complexity of the search space: If the search space is large and complex, we may need to set high values for higher crossover and mutation. It’ll ensure the sufficient exploration of the search space
• The balance between exploration and exploitation: Higher crossover and mutation probabilities can lead to more investigation, while lower chances can lead to more exploitation of known reasonable solutions
• Time and resources available for the search: Higher crossover and mutation probabilities can lead to slower search time. Hence, we may need to readjust the possibilities downward if time or resources are limited
• Problem-specific characteristics and constraints: Some problems come with specific requirements and conditions. We need to consider these conditions when choosing crossover and mutation probabilities

It’s often necessary to experiment with different values for crossover and mutation probabilities to find the optimal values for a particular problem. We can do it using techniques such as parameter tuning or sensitivity analysis.

7. Conclusion

In this tutorial, we discussed two crucial steps in a genetic algorithm: crossover and mutation. We explored how crossover and mutation probabilities can impact the performance of a genetic algorithm.

Finally, we presented some crucial factors that can help us find optimal values for crossover and mutation.