1. Overview
In a previous article, we introduced Prim’s algorithm to find the minimum spanning trees. In this article, we’ll use another approach, Kruskal’s algorithm, to solve the minimum and maximum spanning tree problems.
2. Spanning Tree
A spanning tree of an undirected graph is a connected subgraph that covers all the graph nodes with the minimum possible number of edges. In general, a graph may have more than one spanning tree. The following figure shows a graph with a spanning tree (edges of the spanning tree are in red):
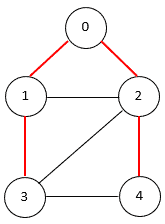
If the graph is edge-weighted, we can define the weight of a spanning tree as the sum of the weights of all its edges. A minimum spanning tree is a spanning tree whose weight is the smallest among all possible spanning trees. The following figure shows a minimum spanning tree on an edge-weighted graph:
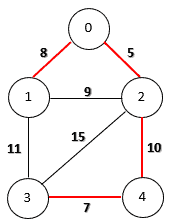
Similarly, a maximum spanning tree has the largest weight among all spanning trees. The following figure shows a maximum spanning tree on an edge-weighted graph:
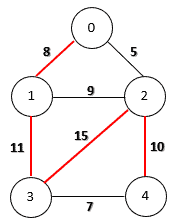
3. Kruskal’s Algorithm
Given a graph, we can use Kruskal’s algorithm to find its minimum spanning tree. If the number of nodes in a graph is V, then each of its spanning trees should have (V-1) edges and contain no cycles. We can describe Kruskal’s algorithm in the following pseudo-code:
Initialize an empty edge set T.
Sort all graph edges by the ascending order of their weight values.
foreach edge in the sorted edge list
Check whether it will create a cycle with the edges inside T.
If the edge doesn't introduce any cycles, add it into T.
If T has (V-1) edges, exit the loop.
return T
Let’s run Kruskal’s algorithm for a minimum spanning tree on our sample graph step-by-step:
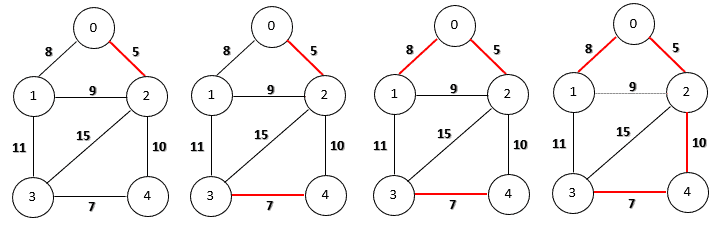
Firstly, we choose the edge (0, 2) because it has the smallest weight. Then, we can add edges (3, 4) and (0, 1) as they do not create any cycles. Now the next candidate is edge (1, 2) with weight 9. However, if we include this edge, we’ll produce a cycle (0, 1, 2). Therefore, we discard this edge and continue to choose the next smallest one. Finally, the algorithm finishes by adding the edge (2, 4) of weight 10.
To calculate the maximum spanning tree, we can change the sorting order to descending order. The other steps remain the same. The following figure shows the step-by-step construction of a maximum spanning tree on our sample graph.
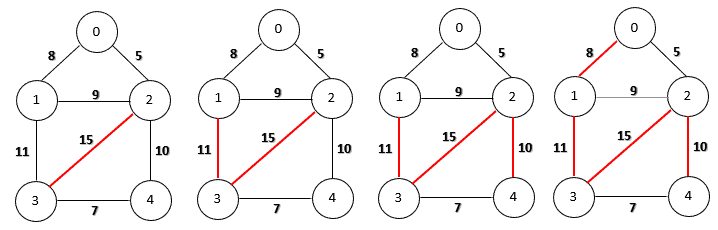
4. Cycle Detection with a Disjoint Set
In Kruskal’s algorithm, the crucial part is to check whether an edge will create a cycle if we add it to the existing edge set. There are several graph cycle detection algorithms we can use. For example, we can use a depth-first search (DFS) algorithm to traverse the graph and detect whether there is a cycle.
However, we need to do a cycle detection on existing edges each time when we test a new edge. A faster solution is to use the Union-Find algorithm with the disjoint data structure because it also uses an incremental edge adding approach to detect cycles. We can fit this into our spanning tree construction process.
4.1. Disjoint Set and Spanning Tree Construction
Firstly, we treat each node of the graph as an individual set that contains only one node. Then, each time we introduce an edge, we check whether its two nodes are in the same set. If the answer is yes, then it will create a cycle. Otherwise, we merge the two disjoint sets into one set and include the edge for the spanning tree.
We can repeat the above steps until we construct the whole spanning tree.
For example, in the above minimum spanning tree construction, we first have 5 node sets: {0}, {1}, {2}, {3}, {4}. When we check the first edge (0, 2), its two nodes are in different node sets. Therefore, we can include this edge and merge {0} and {2} into one set {0, 2}.
We can do similar operations for the edges (3, 4) and (0, 1). The node sets then become {0, 1, 2} and {3, 4}. When we check the next edge (1, 2), we can see that both nodes of this edge are in the same set. Therefore, we discard this edge and continue to check the next one. Finally, the edge (2, 4) satisfies our condition, and we can include it for the minimum spanning tree.
4.2. Disjoint Set Implementation
We can use a tree structure to represent a disjoint set. Each node has a parent pointer to reference its parent node. In each set, there is a unique root node that represents this set. The root node has a self-referenced parent pointer.
Let’s use a Java class to define the disjoint set information:
public class DisjointSetInfo {
private Integer parentNode;
DisjointSetInfo(Integer parent) {
setParentNode(parent);
}
//standard setters and getters
}
Let’s label each graph node with an integer number, starting from 0. We can use a list data structure, List<DisjointSetInfo> nodes, to store the disjoint set information of a graph. In the beginning, each node is the representative member of its own set:
void initDisjointSets(int totalNodes) {
nodes = new ArrayList<>(totalNodes);
for (int i = 0; i < totalNodes; i++) {
nodes.add(new DisjointSetInfo(i));
}
}
4.3. Find Operation
To find the set that a node belongs to, we can follow the node’s parent chain upwards until we reach the root node:
Integer find(Integer node) {
Integer parent = nodes.get(node).getParentNode();
if (parent.equals(node)) {
return node;
} else {
return find(parent);
}
}
It is possible to have a highly unbalanced tree structure for a disjoint set. We can improve the find operation by using the path compression technique.
Since each node we visit on the way to the root node is part of the same set, we can attach the root node to its parent reference directly. The next time when we visit this node, we need one lookup path to get the root node:
Integer pathCompressionFind(Integer node) {
DisjointSetInfo setInfo = nodes.get(node);
Integer parent = setInfo.getParentNode();
if (parent.equals(node)) {
return node;
} else {
Integer parentNode = find(parent);
setInfo.setParentNode(parentNode);
return parentNode;
}
}
4.4. Union Operation
If the two nodes of an edge are in different sets, we’ll combine these two sets into one. We can achieve this union operation by setting the root of one representative node to the other representative node:
void union(Integer rootU, Integer rootV) {
DisjointSetInfo setInfoU = nodes.get(rootU);
setInfoU.setParentNode(rootV);
}
This simple union operation could produce a highly unbalanced tree as we chose a random root node for the merged set. We can improve the performance using a union by rank technique.
Since it is tree depth that affects the running time of the find operation, we attach the set with the shorter tree to the set with the longer tree. This technique only increases the depth of the merged tree if the original two trees have the same depth.
To achieve this, we first add a rank property to the DisjointSetInfo class:
public class DisjointSetInfo {
private Integer parentNode;
private int rank;
DisjointSetInfo(Integer parent) {
setParentNode(parent);
setRank(0);
}
//standard setters and getters
}
In the beginning, a single node disjoint has a rank of 0. During the union of two sets, the root node with a higher rank becomes the root node of the merged set. We increase the new root node’s rank by one only if the original two ranks are the same:
void unionByRank(int rootU, int rootV) {
DisjointSetInfo setInfoU = nodes.get(rootU);
DisjointSetInfo setInfoV = nodes.get(rootV);
int rankU = setInfoU.getRank();
int rankV = setInfoV.getRank();
if (rankU < rankV) {
setInfoU.setParentNode(rootV);
} else {
setInfoV.setParentNode(rootU);
if (rankU == rankV) {
setInfoU.setRank(rankU + 1);
}
}
}
4.5. Cycle Detection
We can determine whether two nodes are in the same disjoint set by comparing the results of two find operations. If they have the same representive root node, then we’ve detected a cycle. Otherwise, we merge the two disjoint sets by using a union operation:
boolean detectCycle(Integer u, Integer v) {
Integer rootU = pathCompressionFind(u);
Integer rootV = pathCompressionFind(v);
if (rootU.equals(rootV)) {
return true;
}
unionByRank(rootU, rootV);
return false;
}
The cycle detection, with the union by rank technique alone, has a running time of O(logV). We can achieve better performance with both path compression and union by rank techniques. The running time is O(α(V)), where α(V) is the inverse Ackermann function of the total number of nodes. It is a small constant that is less than 5 in our real-world computations.
5. Java Implementation of Kruskal’s Algorithm
We can use the ValueGraph data structure in Google Guava to represent an edge-weighted graph.
To use ValueGraph, we first need to add the Guava dependency to our project’s pom.xml file:
<dependency>
<groupId>com.google.guava</groupId>
<artifactId>guava</artifactId>
<version>33.0.0-jre</version>
</dependency>
We can wrap the above cycle detection methods into a CycleDetector class and use it in Kruskal’s algorithm. Since the minimum and maximum spanning tree construction algorithms only have a slight difference, we can use one general function to achieve both constructions:
ValueGraph<Integer, Double> spanningTree(ValueGraph<Integer, Double> graph, boolean minSpanningTree) {
Set<EndpointPair> edges = graph.edges();
List<EndpointPair> edgeList = new ArrayList<>(edges);
if (minSpanningTree) {
edgeList.sort(Comparator.comparing(e -> graph.edgeValue(e).get()));
} else {
edgeList.sort(Collections.reverseOrder(Comparator.comparing(e -> graph.edgeValue(e).get())));
}
int totalNodes = graph.nodes().size();
CycleDetector cycleDetector = new CycleDetector(totalNodes);
int edgeCount = 0;
MutableValueGraph<Integer, Double> spanningTree = ValueGraphBuilder.undirected().build();
for (EndpointPair edge : edgeList) {
if (cycleDetector.detectCycle(edge.nodeU(), edge.nodeV())) {
continue;
}
spanningTree.putEdgeValue(edge.nodeU(), edge.nodeV(), graph.edgeValue(edge).get());
edgeCount++;
if (edgeCount == totalNodes - 1) {
break;
}
}
return spanningTree;
}
In Kruskal’s algorithm, we first sort all graph edges by their weights. This operation takes O(ElogE) time, where E is the total number of edges.
Then we use a loop to go through the sorted edge list. In each iteration, we check whether a cycle will be formed by adding the edge into the current spanning tree edge set. This loop with the cycle detection takes at most O(ElogV) time.
Therefore, the overall running time is O(ELogE + ELogV). Since the value of E is in the scale of O(V2), the time complexity of Kruskal’s algorithm is O(ElogE) or O(ElogV).
6. Conclusion
In this article, we learned how to use Kruskal’s algorithm to find a minimum or maximum spanning tree of a graph. As always, the source code for the article is available over on GitHub.









