1. Overview
In this quick tutorial, we’ll learn how we can detect a cycle in a given directed graph.
2. Graph Representation
For this tutorial, we’ll stick with the adjacency list graph representation.
Firstly, let’s start by defining a Vertex in Java:
public class Vertex {
private String label;
private boolean beingVisited;
private boolean visited;
private List<Vertex> adjacencyList;
public Vertex(String label) {
this.label = label;
this.adjacencyList = new ArrayList<>();
}
public void addNeighbor(Vertex adjacent) {
this.adjacencyList.add(adjacent);
}
//getters and setters
}
Here, the adjacencyList of a vertex v holds a list of all vertices adjacent to v. The addNeighbor() method adds a neighboring vertex to the adjacency list of v.
We’ve also defined two boolean parameters, beingVisited and visited, which represent whether the node is currently being visited or has already been visited.
A graph can be thought of as a group of vertices or nodes connected through the edges.
So, let’s now quickly represent a Graph in Java:
public class Graph {
private List<Vertex> vertices;
public Graph() {
this.vertices = new ArrayList<>();
}
public void addVertex(Vertex vertex) {
this.vertices.add(vertex);
}
public void addEdge(Vertex from, Vertex to) {
from.addNeighbor(to);
}
// ...
}
We’ll use the addVertex() and addEdge() methods to add new vertices and edges in our graph.
3. Cycle Detection
To detect a cycle in a directed graph, we’ll use a variation of DFS traversal:
- Pick up an unvisited vertex v and mark its state as beingVisited
- For each neighboring vertex u of v, check:
- If u is already in the beingVisited state, it clearly means there exists a backward edge and so a cycle has been detected
- If u is yet in an unvisited state, we’ll recursively visit u in a depth-first manner
- Update the vertex v‘s beingVisited flag to false and its visited flag to true
Note that all the vertices of our graph are initially in an unvisited state as both their beingVisited and visited flags are initialized with false.
Let’s now look at our Java solution:
public boolean hasCycle(Vertex sourceVertex) {
sourceVertex.setBeingVisited(true);
for (Vertex neighbor : sourceVertex.getAdjacencyList()) {
if (neighbor.isBeingVisited()) {
// backward edge exists
return true;
} else if (!neighbor.isVisited() && hasCycle(neighbor)) {
return true;
}
}
sourceVertex.setBeingVisited(false);
sourceVertex.setVisited(true);
return false;
}
We can use any vertex in a graph to be the source or the starting vertex.
For a disconnected graph, we’ll have to add an additional wrapper method:
public boolean hasCycle() {
for (Vertex vertex : vertices) {
if (!vertex.isVisited() && hasCycle(vertex)) {
return true;
}
}
return false;
}
This is to ensure that we visit every component of a disconnected graph for detecting a cycle.
4. Implementation Testing
Let’s consider the below cyclic directed graph:
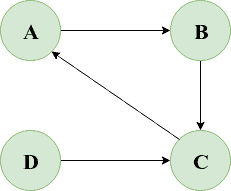
We can quickly write a JUnit to verify our hasCycle() method for this graph:
@Test
void givenGraph_whenCycleExists_thenReturnTrue() {
Vertex vertexA = new Vertex("A");
Vertex vertexB = new Vertex("B");
Vertex vertexC = new Vertex("C")
Vertex vertexD = new Vertex("D");
Graph graph = new Graph();
graph.addVertex(vertexA);
graph.addVertex(vertexB);
graph.addVertex(vertexC);
graph.addVertex(vertexD);
graph.addEdge(vertexA, vertexB);
graph.addEdge(vertexB, vertexC);
graph.addEdge(vertexC, vertexA);
graph.addEdge(vertexD, vertexC);
assertTrue(graph.hasCycle());
}
Here, our hasCycle() method returned true denoting that our graph is cyclic.
5. Conclusion
In this tutorial, we learned how to check if a cycle exists in a given directed graph in Java.
The code backing this article is available on GitHub. Once you're
logged in as a Baeldung Pro Member, start learning and coding on the project.



















