Learn through the super-clean Baeldung Pro experience:
>> Membership and Baeldung Pro.
No ads, dark-mode and 6 months free of IntelliJ Idea Ultimate to start with.
Last updated: March 18, 2024
In this short tutorial, we’ll cover the definition of a heuristic function, its pros and cons, and some of its well-known examples.
A heuristic function (algorithm) or simply a heuristic is a shortcut to solving a problem when there are no exact solutions for it or the time to obtain the solution is too long.
From the definition, we can conclude that the goal is to find a faster solution or an approximate one, even if it is not optimal. In other words, when using a heuristic, we trade accuracy for the speed of the solution.
For example, greedy algorithms usually produce quick but sub-optimal solutions. A greedy algorithm to find the largest sum in the following tree would go for the red path while the optimal path is the green one:
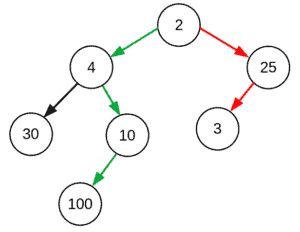
Heuristics don’t always lead to a lower cost. However, those that don’t overestimate the true or the lowest possible cost of a solution are called admissible heuristics. This characteristic can guarantee the optimality of the solution. An admissible heuristic can be found by simplifying the original problem in terms of its constraints, reducing it to a less constrained problem. As an example, let’s consider the eight puzzle problem:
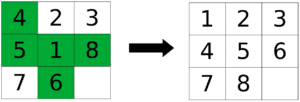
We start from the state on the left, and we want to reach the goal state on the right. As a heuristic solution to this puzzle, we can think of the Hamming distance between the two states, which is the number of misplaced tiles highlighted in green. Here, we have relaxed the constraints of the problem by assuming that we can just pick up a tile and put it in its right place.
This solution is admissible (i.e., it is a lower bound) in that the optimal solution can not have fewer steps than this one.
There are numerous problems for which we can come up with a heuristic algorithm to solve.
Let’s discuss three of the well-known ones.
pathfinding algorithm uses a heuristic to find the shortest path in a graph. Each node
has a cost
which is calculated as
. In this formula,
is the actual cost of the node from the beginning of the path, and
is its heuristic cost to reach the goal.
is admissible, meaning that it always finds the solution with optimal
.
Given a list of cities, in TSP, we want to find the shortest route that visits each city exactly once and returns to the starting city. This is known as an NP-hard problem which means that the optimal solution is hard to find. So instead, we use a greedy algorithm which might not give us the shortest path but at least gives a quick answer.
The greedy algorithm can be considered a heuristic in that although it is a sub-optimal solution, it works reasonably well.
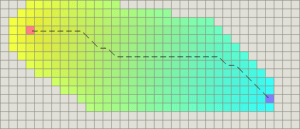
When searching for a path on a grid map, several distance functions can be considered as a heuristic, depending on the constraints for moving directions. This heuristic is then used in the algorithm to find the shortest path. In the images below, we want to go from the orange square to the purple one, and the colored squares are the search space. If any direction is possible, we can use the Euclidean distance:
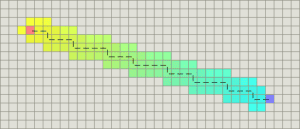
In case of only four directions allowed, the Manhattan distance is an appropriate one:
In this article, we learned about the heuristic function, its benefits and pitfalls, and some of the examples where we can use a heuristic function.