1. Overview
In this tutorial, we’ll take a look at the Java implementation of Boruvka’s algorithm for finding a Minimum Spanning Tree (MST) of an edge-weighted graph.
It predates Prim’s and Kruskal’s algorithms, but still can be considered a cross between the two.
2. Boruvka’s Algorithm
We’ll jump right into the algorithm at hand. Let’s look at a bit of history and then the algorithm itself.
2.1. History
A way to find an MST of a given graph was first formulated by Otakar Boruvka in 1926. This was way before computers even existed, and was in fact modeled to design an efficient electricity distribution system.
Georges Sollin rediscovered it in 1965 and used it in parallel computing.
2.2. The Algorithm
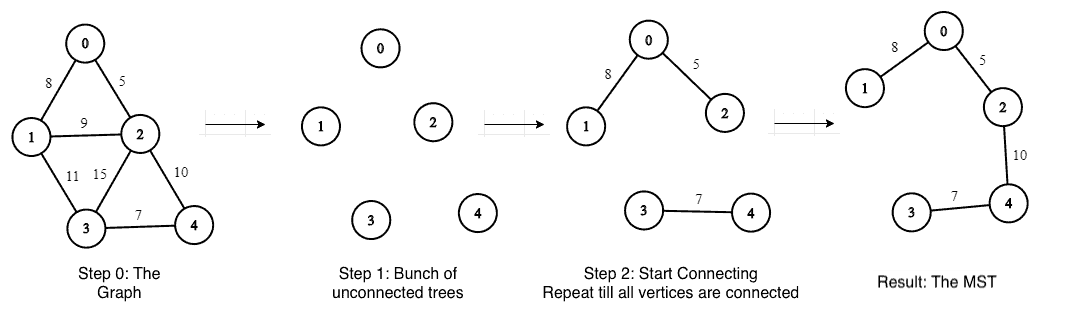
The central idea of the algorithm is to start with a bunch of trees with each vertex representing an isolated tree. Then, we need to keep adding edges to reduce the number of isolated trees until we have a single connected tree.
Let’s see this in steps with an example graph:
- Step 0: create a graph
- Step 1: start with a bunch of unconnected trees (number of trees = number of vertices)
- Step 2: while there are unconnected trees, for each unconnected tree:
- find its edge with lesser weight
- add this edge to connect another tree
3. Java Implementation
Now let’s see how we can implement this in Java.
3.1. The UnionFind Data Structure
To start with, we need a data structure to store the parents and ranks of our vertices.
Let’s define a class UnionFind for this purpose, with two methods: union, and find:
public class UnionFind {
private int[] parents;
private int[] ranks;
public UnionFind(int n) {
parents = new int[n];
ranks = new int[n];
for (int i = 0; i < n; i++) {
parents[i] = i;
ranks[i] = 0;
}
}
public int find(int u) {
while (u != parents[u]) {
u = parents[u];
}
return u;
}
public void union(int u, int v) {
int uParent = find(u);
int vParent = find(v);
if (uParent == vParent) {
return;
}
if (ranks[uParent] < ranks[vParent]) {
parents[uParent] = vParent;
} else if (ranks[uParent] > ranks[vParent]) {
parents[vParent] = uParent;
} else {
parents[vParent] = uParent;
ranks[uParent]++;
}
}
}
We may think of this class as a helper structure for maintaining relationships between our vertices and gradually building up our MST.
To find out whether two vertices u and v belong to the same tree, we see if find(u) returns the same parent as find(v). The union method is used to combine trees. We’ll see this usage shortly.
Now we need a way to get a graph’s vertices and edges from the user and map them to objects we can use in our algorithm at runtime.
Since we’ll use JUnit to test out our algorithm, this part goes in a @Before method:
@BeforeEach
public void setup() {
graph = ValueGraphBuilder.undirected().build();
graph.putEdgeValue(0, 1, 8);
graph.putEdgeValue(0, 2, 5);
graph.putEdgeValue(1, 2, 9);
graph.putEdgeValue(1, 3, 11);
graph.putEdgeValue(2, 3, 15);
graph.putEdgeValue(2, 4, 10);
graph.putEdgeValue(3, 4, 7);
}
Here, we’ve used Guava’s MutableValueGraph<Integer, Integer> to store our graph. Then we used ValueGraphBuilder to construct an undirected weighted graph.
The method putEdgeValue takes three arguments, two Integers for the vertices, and the third Integer for its weight, as specified by MutableValueGraph‘s generic type declaration.
As we can see, this is the same input as shown in our diagram from earlier.
3.3. Derive Minimum Spanning Tree
Finally, we come to the crux of the matter, the implementation of the algorithm.
We’ll do this in a class we’ll call BoruvkaMST. First, let’s declare a couple of instance variables:
public class BoruvkaMST {
private static MutableValueGraph<Integer, Integer> mst = ValueGraphBuilder.undirected().build();
private static int totalWeight;
}
As we can see, we are making use of MutableValueGraph<Integer, Integer> here to represent the MST.
Second, we’ll define a constructor, where all the magic happens. It takes one argument – the graph we built earlier.
The first thing it does is to initialize a UnionFind of the input graph’s vertices. Initially, all vertices are their own parents, each with a rank of 0:
public BoruvkaMST(MutableValueGraph<Integer, Integer> graph) {
int size = graph.nodes().size();
UnionFind uf = new UnionFind(size);
Next, we’ll create a loop that defines the number of iterations required to create the MST – at most log V times or until we have V-1 edges, where V is the number of vertices:
for (int t = 1; t < size && mst.edges().size() < size - 1; t = t + t) {
EndpointPair<Integer>[] closestEdgeArray = new EndpointPair[size];
Here we also initialize an array of edges, closestEdgeArray – to store the closest, lesser-weighted edges.
After that, we’ll define an inner for loop to iterate over all the edges of the graph to populate our closestEdgeArray.
If the parents of the two vertices are the same, it’s the same tree and we don’t add it to the array. Otherwise, we compare the current edge’s weight to the weight of its parent vertices’ edges. If it’s lesser, then we add it to closestEdgeArray:
for (EndpointPair<Integer> edge : graph.edges()) {
int u = edge.nodeU();
int v = edge.nodeV();
int uParent = uf.find(u);
int vParent = uf.find(v);
if (uParent == vParent) {
continue;
}
int weight = graph.edgeValueOrDefault(u, v, 0);
if (closestEdgeArray[uParent] == null) {
closestEdgeArray[uParent] = edge;
}
if (closestEdgeArray[vParent] == null) {
closestEdgeArray[vParent] = edge;
}
int uParentWeight = graph.edgeValueOrDefault(closestEdgeArray[uParent].nodeU(),
closestEdgeArray[uParent].nodeV(), 0);
int vParentWeight = graph.edgeValueOrDefault(closestEdgeArray[vParent].nodeU(),
closestEdgeArray[vParent].nodeV(), 0);
if (weight < uParentWeight) {
closestEdgeArray[uParent] = edge;
}
if (weight < vParentWeight) {
closestEdgeArray[vParent] = edge;
}
}
Then, we’ll define a second inner loop to create a tree. We’ll add edges from the above step to this tree without adding the same edge twice. Additionally, we’ll perform a union on our UnionFind to derive and store parents and ranks of the newly created trees’ vertices:
for (int i = 0; i < size; i++) {
EndpointPair<Integer> edge = closestEdgeArray[i];
if (edge != null) {
int u = edge.nodeU();
int v = edge.nodeV();
int weight = graph.edgeValueOrDefault(u, v, 0);
if (uf.find(u) != uf.find(v)) {
mst.putEdgeValue(u, v, weight);
totalWeight += weight;
uf.union(u, v);
}
}
}
After repeating these steps at most log V times or until we have V-1 edges, the resulting tree is our MST.
4. Testing
Finally, let’s see a simple JUnit to verify our implementation:
@Test
void givenInputGraph_whenBoruvkaPerformed_thenMinimumSpanningTree() {
BoruvkaMST boruvkaMST = new BoruvkaMST(graph);
MutableValueGraph<Integer, Integer> mst = boruvkaMST.getMST();
assertEquals(30, boruvkaMST.getTotalWeight());
assertEquals(4, mst.getEdgeCount());
}
As we can see, we got the MST with a weight of 30 and 4 edges, the same as the pictorial example.
5. Conclusion
In this tutorial, we saw the Java implementation of the Boruvka Algorithm. Its time complexity is O(E log V), where E is the number of edges and V is the number of vertices.
As always, source code is available over on GitHub.





