1. Introduction
Pathfinding algorithms are techniques for navigating maps, allowing us to find a route between two different points. Different algorithms have different pros and cons, often in terms of the efficiency of the algorithm and the efficiency of the route that it generates.
2. What Is a Pathfinding Algorithm?
A Pathfinding Algorithm is a technique for converting a graph – consisting of nodes and edges – into a route through the graph. This graph can be anything at all that needs traversing. For this article, we’re going to attempt to traverse a portion of the London Underground system:
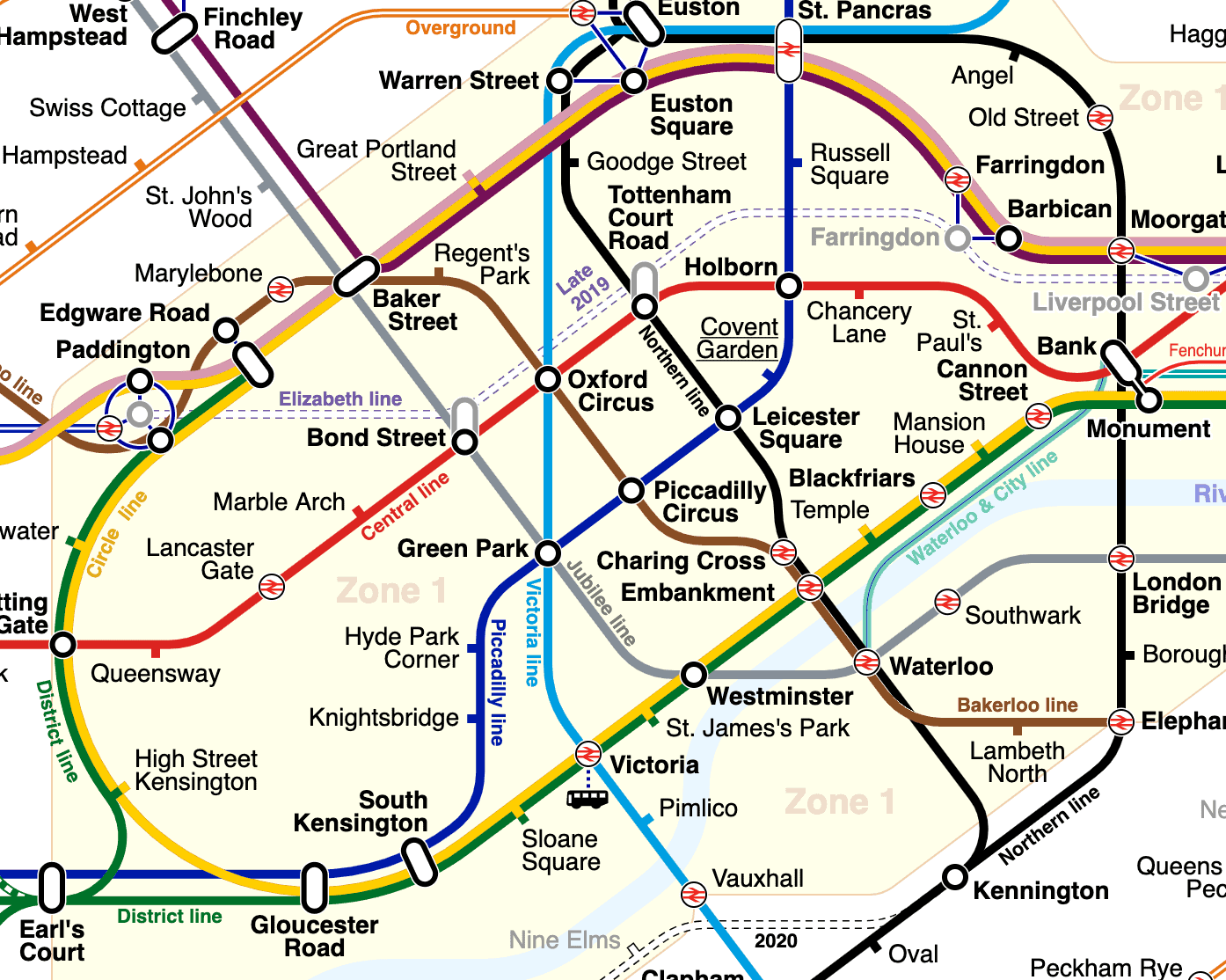
(“London Underground Overground DLR Crossrail map” by sameboat is licensed under CC BY-SA 4.0)
This has a lot of interesting components to it:
- We may or may not have a direct route between our starting and ending points. For example, we can go directly from “Earl’s Court” to “Monument”, but not to “Angel”.
- Every single step has a particular cost. In our case, this is the distance between stations.
- Each stop is only connected to a small subset of the other stops. For example, “Regent’s Park” is directly connected to only “Baker Street” and “Oxford Circus”.
All pathfinding algorithms take as input a collection of all the nodes – stations in our case – and connections between them, and also the desired starting and ending points. The output is typically the set of nodes that will get us from start to end, in the order that we need to go.
3. What Is A*?
A* is one specific pathfinding algorithm, first published in 1968 by Peter Hart, Nils Nilsson, and Bertram Raphael. It is generally considered to be the best algorithm to use when there is no opportunity to pre-compute the routes and there are no constraints on memory usage.
Both memory and performance complexity can be O(b^d) in the worst case, so while it will always work out the most efficient route, it’s not always the most efficient way to do so.
A* is actually a variation on Dijkstra’s Algorithm, where there is additional information provided to help select the next node to use. This additional information does not need to be perfect – if we already have perfect information, then pathfinding is pointless. But the better it is, the better the end result will be.
4. How Does A* Work?
The A* Algorithm works by iteratively selecting what is the best route so far, and attempting to see what the best next step is.
When working with this algorithm, we have several pieces of data that we need to keep track of. The “open set” is all of the nodes that we are currently considering. This is not every node in the system, but instead, it’s every node that we might make the next step from.
We’ll also keep track of the current best score, the estimated total score and the current best previous node for each node in the system.
As part of this, we need to be able to calculate two different scores. One is the score to get from one node to the next. The second is a heuristic to give an estimate of the cost from any node to the destination. This estimate does not need to be accurate, but greater accuracy is going to yield better results. The only requirement is that both scores are consistent with each other – that is, they’re in the same units.
At the very start, our open set consists of our start node, and we have no information about any other nodes at all.
At each iteration, we will:
- Select the node from our open set that has the lowest estimated total score
- Remove this node from the open set
- Add to the open set all of the nodes that we can reach from it
When we do this, we also work out the new score from this node to each new one to see if it’s an improvement on what we’ve got so far, and if it is, then we update what we know about that node.
This then repeats until the node in our open set that has the lowest estimated total score is our destination, at which point we’ve got our route.
4.1. Worked Example
For example, let’s start from “Marylebone” and attempt to find our way to “Bond Street”.
At the very start, our open set consists only of “Marylebone”. That means that this is implicitly the node that we’ve got the best “estimated total score” for.
Our next stops can be either “Edgware Road”, with a cost of 0.4403 km, or “Baker Street”, with a cost of 0.4153 km. However, “Edgware Road” is in the wrong direction, so our heuristic from here to the destination gives a score of 1.4284 km, whereas “Baker Street” has a heuristic score of 1.0753 km.
This means that after this iteration our open set consists of two entries – “Edgware Road”, with an estimated total score of 1.8687 km, and “Baker Street”, with an estimated total score of 1.4906 km.
Our second iteration will then start from “Baker Street”, since this has the lowest estimated total score. From here, our next stops can be either “Marylebone”, “St. John’s Wood”, “Great Portland Street”, Regent’s Park”, or “Bond Street”.
We won’t work through all of these, but let’s take “Marylebone” as an interesting example. The cost to get there is again 0.4153 km, but this means that the total cost is now 0.8306 km. Additionally the heuristic from here to the destination gives a score of 1.323 km.
This means that the estimated total score would be 2.1536 km, which is worse than the previous score for this node. This makes sense because we’ve had to do extra work to get nowhere in this case. This means that we will not consider this a viable route. As such, the details for “Marylebone” are not updated, and it is not added back onto the open set.
5. Java Implementation
Now that we’ve discussed how this works, let’s actually implement it. We’re going to build a generic solution, and then we’ll implement the code necessary for it to work for the London Underground. We can then use it for other scenarios by implementing only those specific parts.
5.1. Representing the Graph
Firstly, we need to be able to represent our graph that we wish to traverse. This consists of two classes – the individual nodes and then the graph as a whole.
We’ll represent our individual nodes with an interface called GraphNode:
public interface GraphNode {
String getId();
}
Each of our nodes must have an ID. Anything else is specific to this particular graph and is not needed for the general solution. These classes are simple Java Beans with no special logic.
Our overall graph is then represented by a class simply called Graph:
public class Graph<T extends GraphNode> {
private final Set<T> nodes;
private final Map<String, Set<String>> connections;
public T getNode(String id) {
return nodes.stream()
.filter(node -> node.getId().equals(id))
.findFirst()
.orElseThrow(() -> new IllegalArgumentException("No node found with ID"));
}
public Set<T> getConnections(T node) {
return connections.get(node.getId()).stream()
.map(this::getNode)
.collect(Collectors.toSet());
}
}
This stores all of the nodes in our graph and has knowledge of which nodes connect to which. We can then get any node by ID, or all of the nodes connected to a given node.
At this point, we’re capable of representing any form of graph we wish, with any number of edges between any number of nodes.
5.2. Steps on Our Route
The next thing we need is our mechanism for finding routes through the graph.
The first part of this is some way to generate a score between any two nodes. We’ll the Scorer interface for both the score to the next node and the estimate to the destination:
public interface Scorer<T extends GraphNode> {
double computeCost(T from, T to);
}
Given a start and an end node, we then get a score for traveling between them.
We also need a wrapper around our nodes that carries some extra information. Instead of being a GraphNode, this is a RouteNode – because it’s a node in our computed route instead of one in the entire graph:
class RouteNode<T extends GraphNode> implements Comparable<RouteNode> {
private final T current;
private T previous;
private double routeScore;
private double estimatedScore;
RouteNode(T current) {
this(current, null, Double.POSITIVE_INFINITY, Double.POSITIVE_INFINITY);
}
RouteNode(T current, T previous, double routeScore, double estimatedScore) {
this.current = current;
this.previous = previous;
this.routeScore = routeScore;
this.estimatedScore = estimatedScore;
}
}
As with GraphNode, these are simple Java Beans used to store the current state of each node for the current route computation. We’ve given this a simple constructor for the common case, when we’re first visiting a node and have no additional information about it yet.
These also need to be Comparable though, so that we can order them by the estimated score as part of the algorithm. This means the addition of a compareTo() method to fulfill the requirements of the Comparable interface:
@Override
public int compareTo(RouteNode other) {
if (this.estimatedScore > other.estimatedScore) {
return 1;
} else if (this.estimatedScore < other.estimatedScore) {
return -1;
} else {
return 0;
}
}
5.3. Finding Our Route
Now we’re in a position to actually generate our routes across our graph. This will be a class called RouteFinder:
public class RouteFinder<T extends GraphNode> {
private final Graph<T> graph;
private final Scorer<T> nextNodeScorer;
private final Scorer<T> targetScorer;
public List<T> findRoute(T from, T to) {
throw new IllegalStateException("No route found");
}
}
We have the graph that we are finding the routes across, and our two scorers – one for the exact score for the next node, and one for the estimated score to our destination. We’ve also got a method that will take a start and end node and compute the best route between the two.
This method is to be our A* algorithm. All the rest of our code goes inside this method.
We start with some basic setup – our “open set” of nodes that we can consider as the next step, and a map of every node that we’ve visited so far and what we know about it:
Queue<RouteNode> openSet = new PriorityQueue<>();
Map<T, RouteNode<T>> allNodes = new HashMap<>();
RouteNode<T> start = new RouteNode<>(from, null, 0d, targetScorer.computeCost(from, to));
openSet.add(start);
allNodes.put(from, start);
Our open set initially has a single node – our start point. There is no previous node for this, there’s a score of 0 to get there, and we’ve got an estimate of how far it is from our destination.
The use of a PriorityQueue for the open set means that we automatically get the best entry off of it, based on our compareTo() method from earlier.
Now we iterate until either we run out of nodes to look at, or the best available node is our destination:
while (!openSet.isEmpty()) {
RouteNode<T> next = openSet.poll();
if (next.getCurrent().equals(to)) {
List<T> route = new ArrayList<>();
RouteNode<T> current = next;
do {
route.add(0, current.getCurrent());
current = allNodes.get(current.getPrevious());
} while (current != null);
return route;
}
// ...
When we’ve found our destination, we can build our route by repeatedly looking at the previous node until we reach our starting point.
Next, if we haven’t reached our destination, we can work out what to do next:
graph.getConnections(next.getCurrent()).forEach(connection -> {
RouteNode<T> nextNode = allNodes.getOrDefault(connection, new RouteNode<>(connection));
allNodes.put(connection, nextNode);
double newScore = next.getRouteScore() + nextNodeScorer.computeCost(next.getCurrent(), connection);
if (newScore < nextNode.getRouteScore()) {
nextNode.setPrevious(next.getCurrent());
nextNode.setRouteScore(newScore);
nextNode.setEstimatedScore(newScore + targetScorer.computeCost(connection, to));
openSet.add(nextNode);
}
});
throw new IllegalStateException("No route found");
}
Here, we’re iterating over the connected nodes from our graph. For each of these, we get the RouteNode that we have for it – creating a new one if needed.
We then compute the new score for this node and see if it’s cheaper than what we had so far. If it is then we update it to match this new route and add it to the open set for consideration next time around.
This is the entire algorithm. We keep repeating this until we either reach our goal or fail to get there.
5.4. Specific Details for the London Underground
What we have so far is a generic A* pathfinder, but it’s lacking the specifics we need for our exact use case. This means we need a concrete implementation of both GraphNode and Scorer.
Our nodes are stations on the underground, and we’ll model them with the Station class:
public class Station implements GraphNode {
private final String id;
private final String name;
private final double latitude;
private final double longitude;
}
The name is useful for seeing the output, and the latitude and longitude are for our scoring.
In this scenario, we only need a single implementation of Scorer. We’re going to use the Haversine formula for this, to compute the straight-line distance between two pairs of latitude/longitude:
public class HaversineScorer implements Scorer<Station> {
@Override
public double computeCost(Station from, Station to) {
double R = 6372.8; // Earth's Radius, in kilometers
double dLat = Math.toRadians(to.getLatitude() - from.getLatitude());
double dLon = Math.toRadians(to.getLongitude() - from.getLongitude());
double lat1 = Math.toRadians(from.getLatitude());
double lat2 = Math.toRadians(to.getLatitude());
double a = Math.pow(Math.sin(dLat / 2),2)
+ Math.pow(Math.sin(dLon / 2),2) * Math.cos(lat1) * Math.cos(lat2);
double c = 2 * Math.asin(Math.sqrt(a));
return R * c;
}
}
We now have almost everything necessary to calculate paths between any two pairs of stations. The only thing missing is the graph of connections between them.
Let’s use it for mapping out a route. We’ll generate one from Earl’s Court up to Angel. This has a number of different options for travel, on a minimum of two tube lines:
public void findRoute() {
List<Station> route = routeFinder.findRoute(underground.getNode("74"), underground.getNode("7"));
System.out.println(route.stream().map(Station::getName).collect(Collectors.toList()));
}
This generates a route of Earl’s Court -> South Kensington -> Green Park -> Euston -> Angel.
The obvious route that many people would have taken would likely be Earl’s Count -> Monument -> Angel, because that’s got fewer changes. Instead, this has taken a significantly more direct route even though it meant more changes.
6. Conclusion
In this article, we’ve seen what the A* algorithm is, how it works, and how to implement it in our own projects. Why not take this and extend it for your own uses?
Maybe try to extend it to take interchanges between tube lines into account, and see how that affects the selected routes?
And again, the complete code for the article is available over on GitHub.





