1. Overview
In this tutorial, we’ll discuss a unique graph data structure: a tournament graph. We’ll present the definition and properties of tournament graphs with examples.
Finally, we’ll highlight some advantages and disadvantages of it.
2. Definition
Tournament graphs are versatile graph structures used in various fields, including computer science, mathematics, social sciences, and game theory. Their unique properties and simple structure make them suitable for modeling and analyzing complex problems.
Let’s define a tournament graph. It’s a directed graph in which a single directed edge connects each pair of distinct vertices in one of the two possible directions.
In other words, a tournament graph is a complete graph where each edge is directed either from one vertex to the other or vice versa.
We often use tournament graphs to model situations where pairs of competitors face off against each other in a series of one-on-one matches, such as in a round-robin tournament.
Additionally, the direction of the edges in the graph represents the outcome of each match, with an edge pointing from the winner to the loser.
3. Properties
Tournament graphs have several important and unique properties. Let’s discuss them.
A tournament graph is a strongly connected graph. Therefore, the graph has a directed path from any vertex to any other vertex. A single directed edge in one of the two possible directions connects every pair of vertices in the graph.
Another interesting property is that every tournament graph contains a unique hamiltonian path. A hamiltonian path visits every vertex exactly once. Therefore, we can order the edges in a tournament graph in such a way that the direction of the edges alternates, creating a path that visits each vertex exactly once.
Furthermore, every tournament graph follows the transitive relation property. Hence, if vertex A beats vertex B, and vertex B beats vertex C, then vertex A must also beat vertex C. Additionally, we can follow this property from the fact that the edges in the graph are directed. Therefore, there’s only one edge between each pair of vertices.
4. Example
Now we know the definition and properties of tournament graphs. Let’s take some sample graphs. Here, our aim is to correctly identify the tournament graphs from the sample graphs.
Let’s look at the first graph :
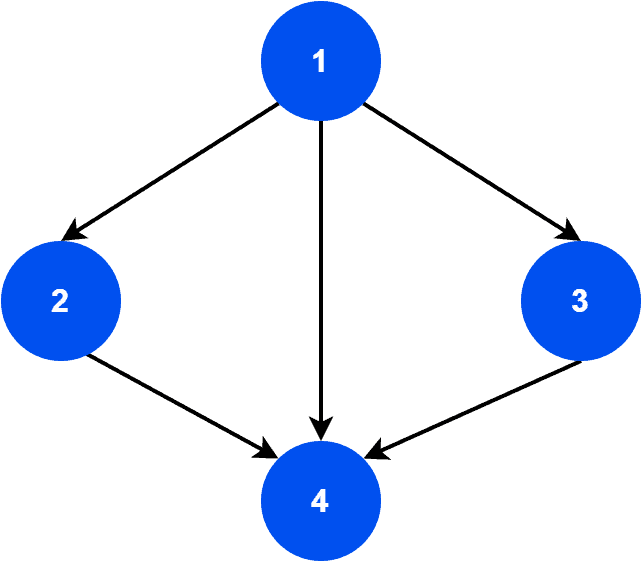
As we can see, graph is a directed graph. A tournament graph should be strongly connected. Hence, the graph must have a directed path from any vertex to any other vertex. However, in
, we can’t reach vertex 2 via vertex 3. Therefore, we can conclude that graph
is not a tournament graph.
Furthermore, let’s take a look at the second sample graph:
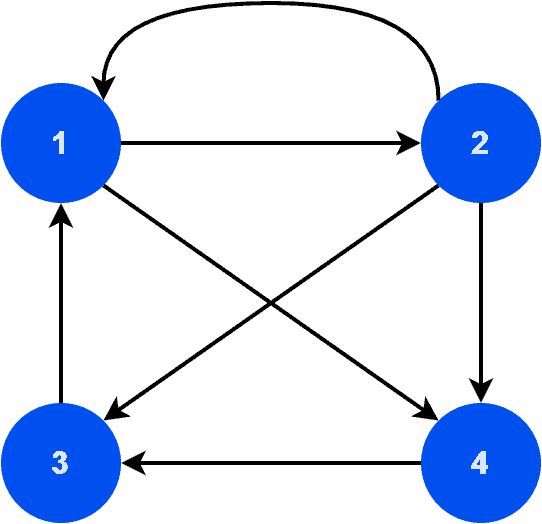
Graph is a directed, strongly connected, and complete graph. However, as we can see, there’s a parallel edge from vertex 2 to vertex 1. Tournament graphs don’t contain parallel edges. Hence, graph
is also not a tournament graph.
Let’s take a look at the final sample graph :
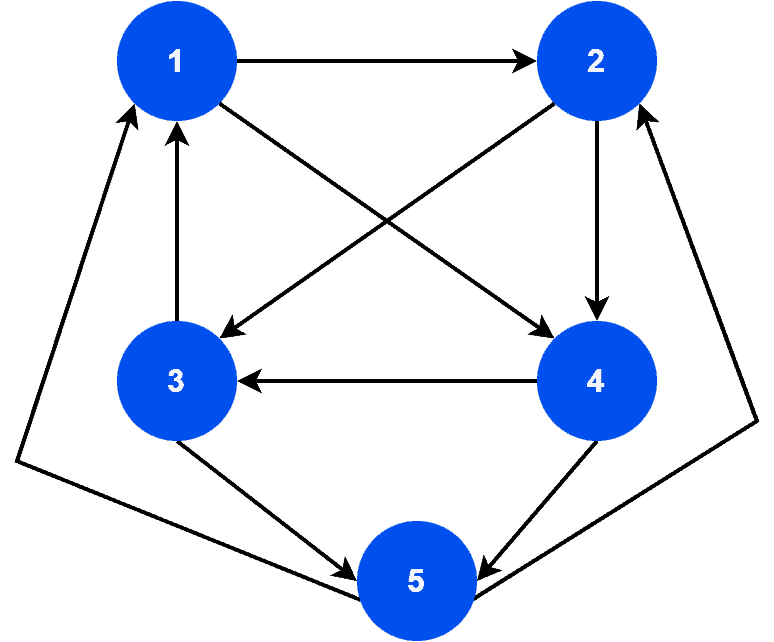
We can easily verify that is strongly connected, as well as a complete graph. Additionally,
doesn’t contain any parallel edges. Furthermore, it contains a unique hamiltonian path: 12435. Hence, we can conclude that
is a tournament graph.
5. Advantages and Disadvantages
Due to the unique graph structure, tournament graphs have several advantages. Let’s discuss the core benefits.
First of all, tournament graphs are easy to construct. We can generate them using various algorithms. Hence, this makes them useful in various applications such as randomization and simulation.
Tournament graphs are robust. They can tolerate errors or failures without completely losing their properties. Due to such benefits, we can use them in various applications, such as fault-tolerant routing and distributed computing.
Finally, as tournament graphs are strongly connected, there’s a directed path between any two vertices in the graph. As a result of strong connectivity, we utilize these graphs in various applications, such as network routing.
While tournament graphs have many advantages, they also have some limitations. Let’s discuss some of the significant disadvantages.
Every vertex in a tournament graph has a high degree of connectivity. Therefore, it can be challenging to analyze and manage a large graph. For example, finding efficient routing algorithms or searching in such graphs can be difficult.
Tournament graphs are directed graphs. Therefore, they may not be suitable for applications that require undirected graphs. For example, if the edges between vertices in a graph represent mutual relationships, such as friendships, a tournament graph may not accurately represent the relationships.
We mainly use tournament graphs for representing ranking or sorting relationships. However, this graph structure may not be suitable for other types of data. For example, if the edges in a graph represent distance or similarity, a tournament graph may not be the best representation.
6. Conclusion
In this tutorial, we discussed a unique graph data structure: a tournament graph. We presented the definition and properties of tournament graphs with examples.
Finally, we highlighted some advantages and disadvantages of this graph structure.