1. Introduction
Machine learning (ML) is a branch of computer science and artificial intelligence that allows computer programs to learn without being explicitly programmed. In brief, ML includes a set of algorithms based on statistical techniques that can learn from data to make some decisions or predictions.
Input data usually consist of a set of input features or variables. When the ML model outputs prediction, it relies more on some features than others. Consequently, some features are more important to the model and some less.
In this tutorial, we’ll explain what is feature (variable) importance, with some examples, and how to measure it.
2. 2. What Are the Features in Machine Learning?
Explained in one sentence, features or variables are individual properties generated from a data set and used as input to ML models. Overall, we represent features as numerical columns in data sets, but they can also be strings. For instance, the table below represents some features like goals, height, position, and salary that describe soccer players.
Features are one of the most important components in ML modeling. Basically, model predictions directly depend on the quality of features. As a result, in ML, a special emphasis is placed on feature engineering and feature selection. To know which features contribute more to the model and, provided that, select or create new features, we would need to measure their importance somehow.
3. 3. What Is Feature Importance in Machine Learning?
Feature (variable) importance indicates how much each feature contributes to the model prediction. Basically, it determines the degree of usefulness of a specific variable for a current model and prediction. For example, if we want to predict the weight of a person based on height, age, and name, it’s obvious that the variable height will have the strongest influence, while the variable name is not even relevant to the person’s weight.
Overall, we represent feature importance using a numeric value that we call the score, where the higher the score value has, the more important it is. There are many benefits of having a feature importance score. For instance, it’s possible to determine the relationship between independent variables (features) and dependent variables (targets). By analyzing variable importance scores, we would be able to find out irrelevant features and exclude them. Reducing the number of not meaningful variables in the model may speed up the model or even improve its performance.
Also, feature importance is commonly used as a tool for ML model interpretability. From the scores, it’s possible to explain why the ML model makes particular predictions and how we can manipulate features to change its predictions.
There are many ways of calculating feature importance, but generally, we can divide them into two groups:
- Model agnostic
- Model dependent
In this article, we’ll explain only some of them.
4. Model Agnostic Feature Importance
This group of methods is not specifically related to one particular ML method but can be applied to most of the ML models that solve one problem. For instance, if we solve a classification problem, we can apply model agnostic methods to all ML algorithms such as logistic regression, random forest, support vector machine, and others.
4.1. Correlation Criteria
Firstly, the most simple way to measure the feature importance is to correlate them with target variables. This is possible when the target has continuous value. Basically, correlation is a statistical measurement that quantifies the relationship between two variables. The most popular correlation methods are Pearson and Spearman correlation. Pearson correlation measures linear dependence between two variables while Spearman measures monotonicity, and they both might assume values between -1 and 1:
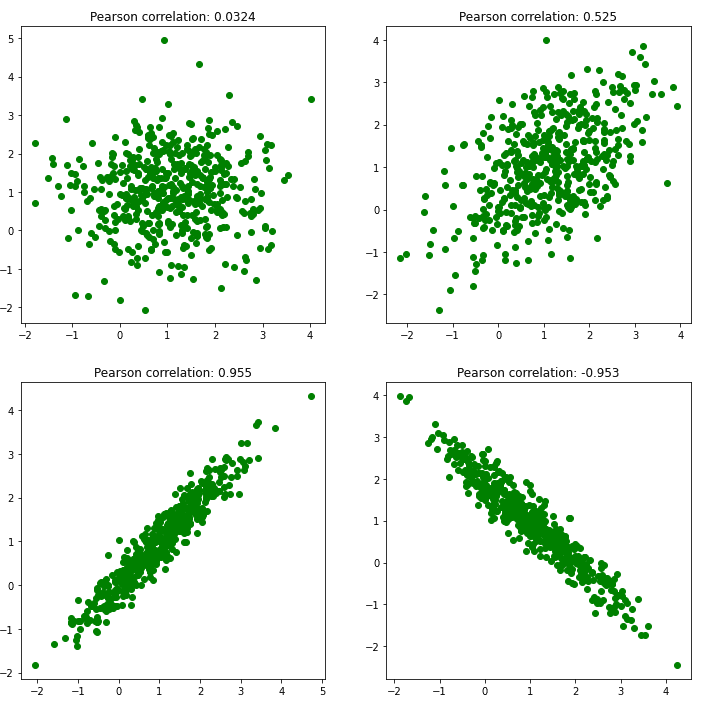
The idea of measuring feature importance is pretty simple. All we need is to measure the correlation between each feature and the target variable. Also, if there are more target variables, we might calculate average correlation as an importance indicator. After that, features with a higher absolute value of a correlation coefficient are more important.
4.2. Single Variable Prediction
Instead of using the correlation coefficient as a feature importance score, we can simply use the individual feature as an input to a model. Then, based on its prediction, it’s possible to consider feature individual prediction power as feature importance. Depending on the ML problem, it’s even possible to define multiple measurements, such as different error and accuracy-based metrics, and moreover, combine them.
However, we don’t need to interpret an individual prediction power as ground truth for variable importance. Sometimes might happen that the variable has a low individual prediction power, but when combined with other variables, it might add a significant performance improvement to the model.
4.3. Permutation Feature Importance
Permutation feature importance is, in the first place, a pretty simple and commonly used technique. Basically, the whole idea is to observe how predictions of the ML model change when we change the values of a single variable. We do this by applying permutations to a single algorithm. The algorithm is as follows:
5. Model Dependent Feature Importance
Model-dependent feature importance is specific to one particular ML model. Basically, in most cases, they can be extracted directly from a model as its part. But despite that, we can use them as separate methods for feature importance without necessarily using that ML model for making predictions.
5.1. Linear Regression Feature Importance
We can fit a linear regression model and then extract coefficients that will show the importance of each input variable. The assumption is that the input features have the same scale or were scaled before fitting a model. The same features scale is needed to compare the magnitude of these coefficients and conclude which features are more important.
Besides simple linear regression, a linear regression with an L1 regularization parameter, called Lasso regression, is commonly used, especially for feature selection. Lasso regression has regularization parameter that controls the degree of regularization and shrinks the coefficients to become smaller. Also, Lasso might arbitrarily shrink correlated variables by selecting only one of them.
5.2. Decision Tree Feature Importance
Decision tree algorithms provide feature importance scores based on reducing the criterion used to select split points. Usually, they are based on Gini or entropy impurity measurements. Also, the same approach can be used for all algorithms based on decision trees such as random forest and gradient boosting.
6. Conclusion
In this article, we’ve explained the term features in ML. Also, we’ve presented features importance as well as some types of features importance methods. To conclude, feature importance is a commonly used technique since it allows us to learn a lot of new information about our ML models and, based on that, decide on the next steps in the modeling.