K-Means for Classification | Baeldung on Computer Science

1. Introduction

In this tutorial, we’ll talk about using the K-Means clustering algorithm for classification.

2. Clustering vs. Classification

Clustering and classification are two different types of problems we solve with Machine Learning. In the classification setting, our data have labels, and our goal is to learn a classifier that can accurately label those and other data points. In contrast, when we do clustering, the data aren’t labeled, and we aim to group instances into clusters by their similarity.

However, clustering algorithms, such as K-Means, can be integrated with a classifier or train one.

3. K-Means as a Preprocessing Step

Let’s imagine a set of unlabeled data:

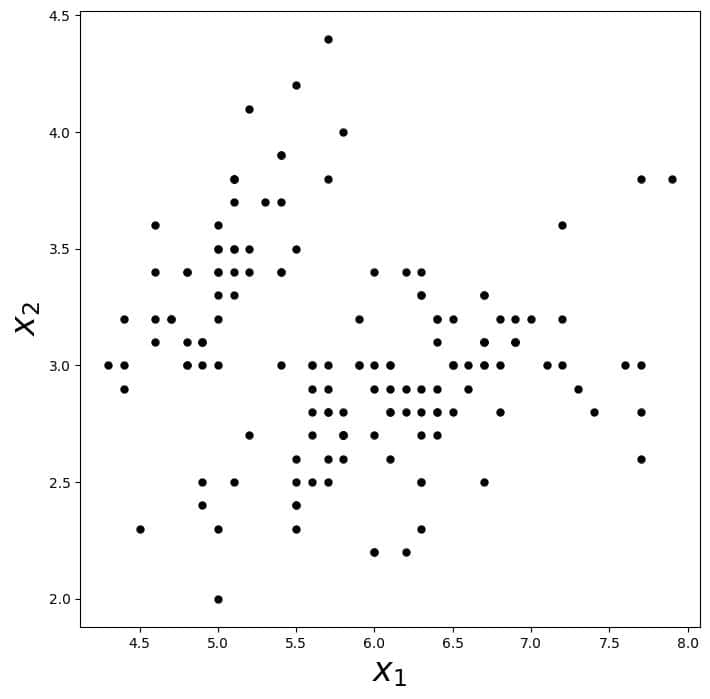
It’s the iris dataset. The $x_1$ axis is sepal length, and $x_2$ is sepal width.

Now, we don’t have access to the labels but know that the instances belong to two or more classes. In this case, we first cluster the data with K-Means and then treat the clusters as separate classes. This way, we can label all the data (by assigning the instances to the closest cluster), preparing the dataset for training a classifier.

So, we first learn the class labels from the data and then train a classifier to discriminate between the classes discovered while clustering.

For example, K-Means finds these three clusters (classes) and centroids in the above data:

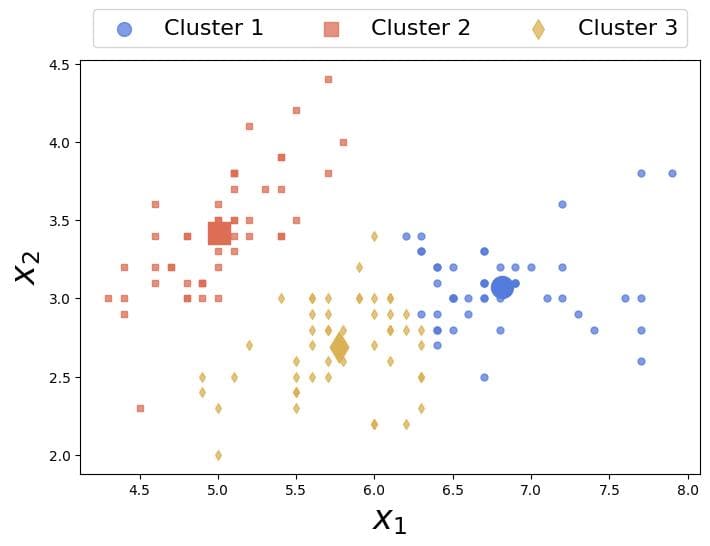Then, we could train a neural network to differentiate between the three classes.

4. A Simple K-Means Classifier

We don’t have to train a classifier on top of the clustered data. Instead, we can use the clusters’ centroids for classification. The labeling rule is straightforward. Find the closest centroid and assign the new instance to that cluster:

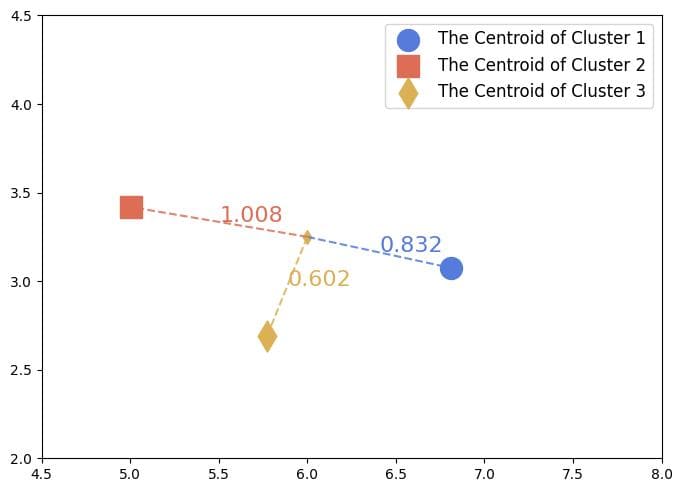
Since the third cluster’s center is the closest to the instance in between the clusters, we give it the label $y=3$ .

5. Problems

The data weren’t labeled in the previous two methods. So, we used K-Means to learn the labels and built a classifier on top of its results by assuming that the clustering errors were negligible.

The assumption, however, may not hold. K-Means requires us to choose the number of clusters in advance. We can go with the elbow heuristic to decide how many clusters to have, but we could be wrong. Even if we identify the correct number of classes, the labels we get with K-Means may be incorrect. That can happen if the distance metric we use doesn’t reflect the similarity between the same-labeled instances.

Unfortunately, this issue is something we can’t resolve. Since we start from the unlabeled data, there’s no ground truth with which we can compare the results of K-Means.

We should also keep in mind that if we discover classes with K-Means or any other clustering algorithm, it’s up to us to determine what each represents.

6. K-Means Classification

If our data is labeled, we can still use K-Means, even though it’s an unsupervised algorithm. We only need to adjust the training process. Since now we do have the ground truth, we can measure the quality of clustering via the actual labels. Even more so, we don’t have to guess the number of clusters–we set it to the number of classes.

Once we identify the clusters, we classify a new object by its proximity to the centroids.

6.1. The Unsupervised K-Means

Formally, let $\{ (x_i, y_i)\}_{i=1}^{n}$ be our dataset, where the $x_i$ are objects, and the $y_i \in \{1,2,\ldots,d\}$ are their labels. In the usual K-Means, we form $d$ clusters by minimizing the withing-group distances. If $\mathcal{C}_j$ is the $j$ th cluster and the number of instances in it, we find the centroids by minimizing:

(1) $\begin{equation*} J(c_1, c_2, \ldots, c_d) = \sum_{j=1}^{d}\frac{1}{n_j}\sum_{i : x_i \in \mathcal{C}_j} ||x_i - c_j||^2 \end{equation*}$

We can do that using, e.g., the Expectation-Maximization algorithm.

6.2. The Supervised K-Means Impurity

However, since we know the $y_i$ , we can also aim to maximize the purity of $\boldsymbol{C_1, C_2, \ldots, C_d}$ . The goal is to have each class appear in only one cluster.

For example, the Gini impurity index tells us how heterogeneous a cluster is:

$G_j = 1 - \sum_{k=1}^{d} \left( \frac{n_{k, j}}{n_j} \right)^2 \qquad n_{k, j} = \left| \{ x_{\ell} \in C_j : y_{\ell} = k \} \right| \quad j=1,2,\ldots,d$

We can minimize the probability of error by minimizing the average index even though we don’t explicitly optimize accuracy or the error risk:

(2) $\begin{equation*} \frac{1}{d}\sum_{j=1}^{d}G_j \end{equation*}$

That’s because we’ll try to force all the instances of the same class into a single cluster, which will separate the classes as much as possible.

We can also combine the average Gini index with the inter-cluster distances. That way, we minimize the withing-cluster distances and the error probability at the same time:

(3) $\begin{equation*} J(c_1, c_2, \ldots, c_d) = \left( \sum_{j=1}^{d}\frac{1}{n_j}\sum_{i : x_i \in \mathcal{C}_j} ||x_i - c_j||^2 \right) + \frac{1}{d}\sum_{j=1}^{d}G_j \end{equation*}$

6.3. Clustering as Regularization

It’s interesting to note that K-Means acts as a regularization technique. Since it forms clusters by grouping near objects, the training process has an incentive to find geometrically well-shaped groups. That could prevent overfitting.

To control the trade-off between accuracy and generalization capability, we can include a regularization coefficient $\lambda > 0$ into the objective function (3):

(4) $\begin{equation*} J(c_1, c_2, \ldots, c_d) = \lambda \left( \sum_{j=1}^{d}\frac{1}{n_j}\sum_{i : x_i \in \mathcal{C}_j} ||x_i - c_j||^2 \right) + \frac{1}{d}\sum_{j=1}^{d}G_j \end{equation*}$

A higher $\boldsymbol{\lambda}$ means that we’re more interested in compact shapes than purity, whereas lower values put more weight on minimizing the classification error.

7. Conclusion

In this article, we showed how to use K-means for classification. Even though it’s an unsupervised clustering algorithm, we can apply it to classification problems.

Full Archive

About Baeldung

Core Concepts

Operating Systems

Artificial Intelligence

Graph Theory

Latex